
2场的唯一性定理 。场的唯一性定理 在以上三种边界条件下,满足Laplace方程和Poisson方 程的电位函数是唯一的。 。利用格林第一公式来证明这一定理。 LVvovlajo (4.2-1) ·若p1、p2都满足拉氏方程(或Poisson方程),则 p'=p1-p2满足Laplace方程,即: V20'=0 (4.2-2) 6
2 场的唯一性定理 场的唯一性定理 在以上三种边界条件下,满足Laplace方程和Poisson方 程的电位函数是唯一的。 利用格林第一公式来证明这一定理。 若 、 都满足拉氏方程(或Poisson方程),则 满足Laplace方程,即: ( ) + = V S dS n dV 2 1 2 = 1 −2 0 2 = (4.2-1) (4.2-2) 6

2场的唯一性定理 令格林公式中p、"都是0',则: Lvofav=fo品s (4.2-3) ·第一种情况(Dirichlet问题): 4、2在S上均满足第一类边界条件,则p、=0 ∫p1dw=0 (4.2-4) .Vo2≥0 而积分为0→V0'=0 。 p'=C(常数) 而在S上0'=0∴.p≡0 ∴.p1=p2 7
2 场的唯一性定理 令格林公式中 、 都是 ,则: 第一种情况(Dirichlet问题): 、 在S上均满足第一类边界条件,则 ∴ ∵ 而积分为0 ∴ 而在S上 ∴ ∴ = V S dS n dV 2 1 2 = 0 S 0 2 = V dV 0 2 = 0 = C (常数) = 0 0 1 = 2 (4.2-3) (4.2-4) 7

2场的唯一性定理 。第二种情况(Neumann问题): 0、02都满足 = Ψo on 则: 001 602 =0 on s On On 故(4.2-3)右边=0,同样可得:9,-p2=C(常数) 在参考点处01=p2=0,故01-02=0 .p1=02 。第三种情况(Mixed问题)证明与第二种情况类似,略。 8
2 场的唯一性定理 第二种情况(Neumann问题): 、 都满足 则: 故(4.2-3)右边=0,同样可得: ∵ 在参考点处 ,故 ∴ 第三种情况(Mixed问题)证明与第二种情况类似,略。 1 2 0 = S n 0 1 2 = − = S S S n n n − = C (常数) 1 2 1 = 2 = 0 1 −2 0 1 = 2 8

2场的唯一性定理 。唯一性定理的重要意义 一是告诉我们在什么条件下得到的解是唯一的: ·二是无论用何种方法找到一个函数,既满足微分方程, 又满足问题特定的边界条件,则它必是该问题的解。即 可以灵活的选择求解方法: 三是根据唯一性定理,可以建立许多应用于电磁场问题 求解的等效原理。 9
2 场的唯一性定理 唯一性定理的重要意义 一是告诉我们在什么条件下得到的解是唯一的; 二是无论用何种方法找到一个函数,既满足微分方程, 又满足问题特定的边界条件,则它必是该问题的解。即 可以灵活的选择求解方法; 三是根据唯一性定理,可以建立许多应用于电磁场问题 求解的等效原理。 9
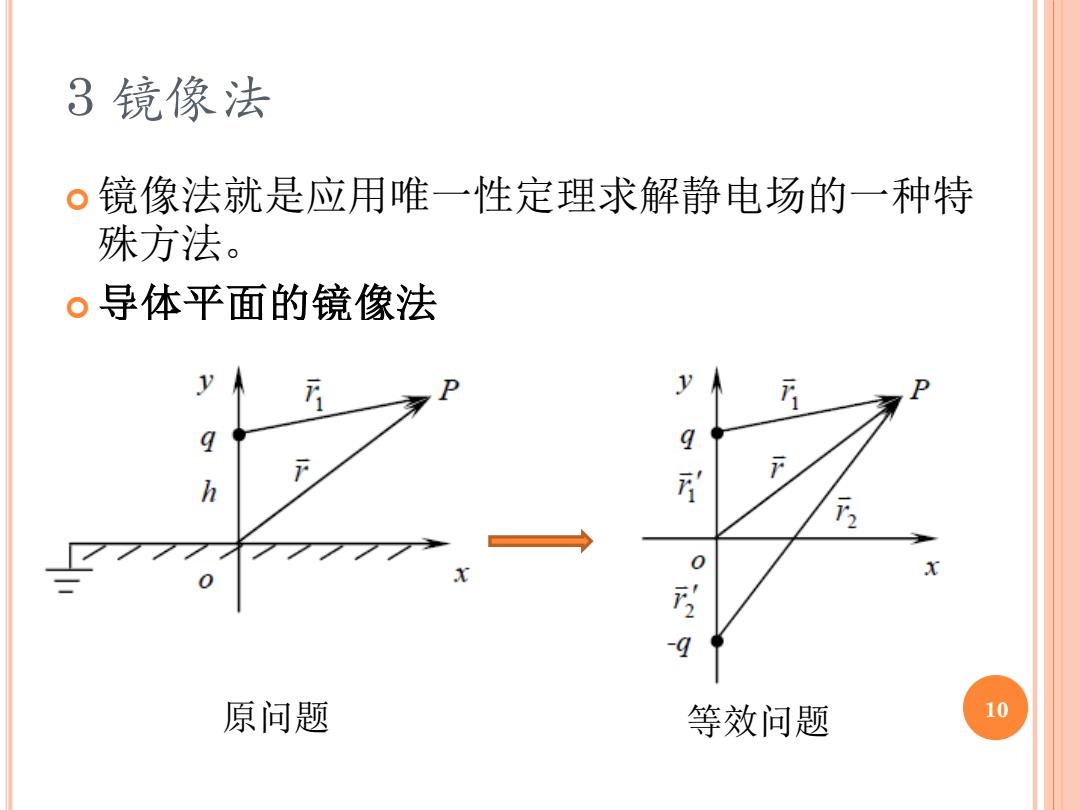
3镜像法 。镜像法就是应用唯一性定理求解静电场的一种特 殊方法。 。导体平面的镜像法 h 2 x 原问题 等效问题 10
3 镜像法 镜像法就是应用唯一性定理求解静电场的一种特 殊方法。 导体平面的镜像法 原问题 等效问题 10