南京农业大学：《生物统计与田间试验》课程教学资源（PPT课件）第十三章 多因素试验结果的统计分析

表13.22三因素随机区组设计的期望均方 期望均方 变异来 源 DF MS 固定模 随机模型 混合模型 型 A、B固定，C随机 区组间 -1 o2+abexp o2+abco d2+abckgoro2+abco A a-1 MS 2+++rco+rboic+rbco G2+broc+rbcx月 B b-1 SSg o2+rack +roc+rc+raoic+raco 2 o2+raoic+racx话 C c-1 SSc 2+rabkdo+ranc+rboic+rac ic+rabac o2+raboc AXB (a-1)(b-1) SSAB G2+rck 2+ranc+rcon 2+roinc+rc AXC (a-1)(c-1) SSAC a2 +rbxic o2+roinc +rbaic o2+rboac BXC (b-1)(c-1) SSBC G+raK BC 2+roanc+raoic 2 2+raoic (a-1) AXBX (b-1)(c-1) +rKC 2+raBc 02+roABC 2 SSABC 误差 abc (n-1) SS。 02 02

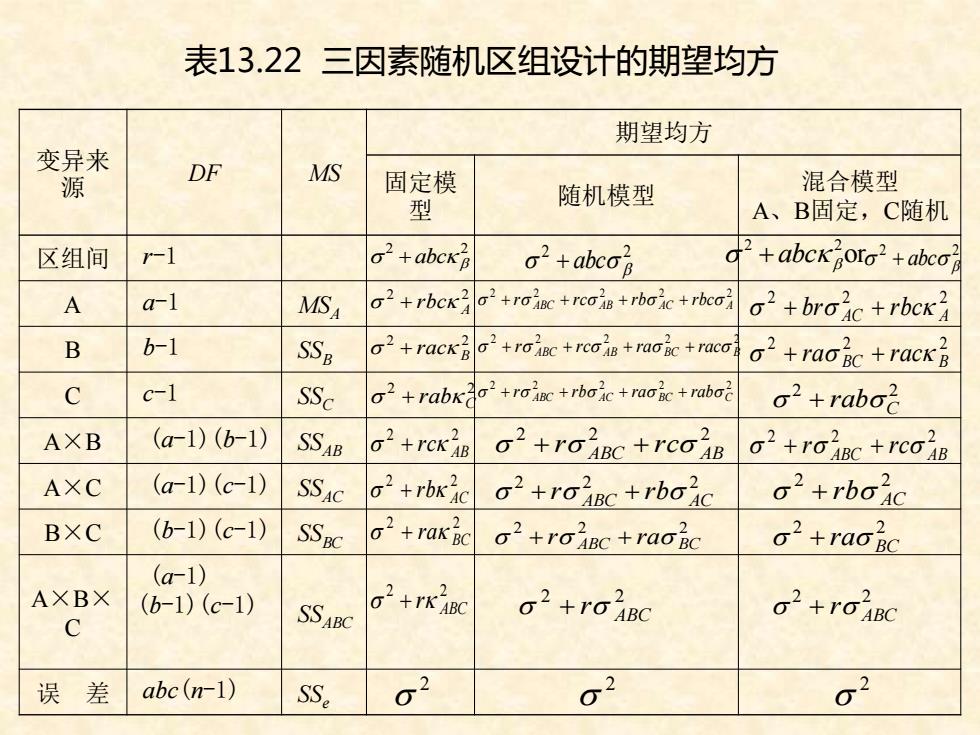
变异来 源 DF MS 期望均方 固定模 型 随机模型 混合模型 A、B固定，C随机 区组间 r-1 A a-1 MSA B b-1 SSB C c-1 SSC A×B (a-1)(b-1) SSAB A×C (a-1)(c-1) SSAC B×C (b-1)(c-1) SSBC A×B× C (a-1) (b-1)(c-1) SSABC 误 差 abc(n-1) SSe 表13.22 三因素随机区组设计的期望均方 2 2  + abc  2 2 A  + rbc 2 2 B  + rac 2 2 C  + rab 2 2 AB  + rc 2 2 AC  + rb 2 2 BC  + ra 2 2 ABC  + r 2  2  2  2 2    + abc 2 2 2 2 2 ABC AB AC A  + r + rc + rb + rbc 2 2 2 2 2 ABC AB BC B  + r + rc + ra + rac 2 2 2 2 2 ABC AC BC C  + r + rb + ra + rab 2 2 2 ABC AB  + r + rc 2 2 2 ABC AC  + r + rb 2 2 2 ABC BC  + r + ra 2 2 ABC  + r or 2 2  + abc  2 2    + abc 2 2 2 AC A  + br + rbc 2 2 2 BC B  + ra + rac 2 2 C  + rab 2 2 2 ABC AB  + r + rc 2 2 AC  + rb 2 2 BC  + ra 2 2 ABC  + r

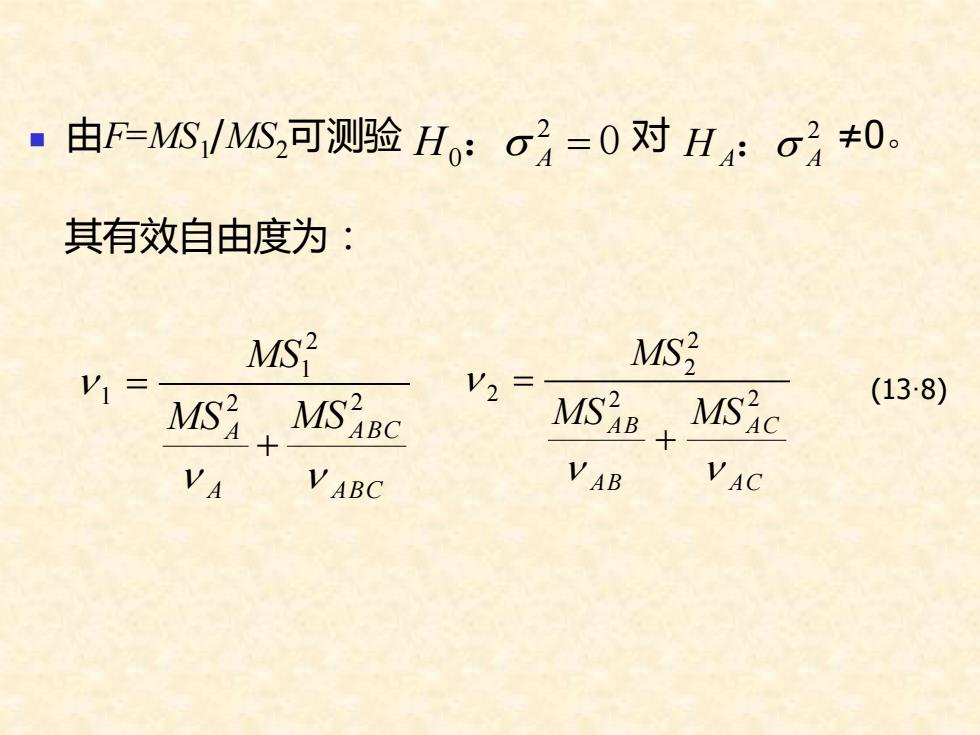
·由F=MS,/MS,可测验Ho:o月=0对H4:o?+0 其有效自由度为： MS2 MS子 V1= MS'BC V2= NS2B+ (138) VA VABC VAB V AC

◼ 由F=MS1 /MS2可测验 对 ≠0。 其有效自由度为： ： = 0 2 H0  A 2 H A ： A ABC ABC A MS A MS MS    2 2 2 1 1 + = A C A C A B MS A B MS MS    2 2 2 2 2 + = (13·8)

第二节 裂区试验的统计分析 ■一、裂区试验结果统计分析示例 ■二、裂区试验的缺区估计 ■三、裂区试验的线性模型和期望均方 ■四、再裂区设计的分析 ■五、条区设计的分析

第二节 裂区试验的统计分析 ◼ 一、裂区试验结果统计分析示例 ◼ 二、裂区试验的缺区估计 ◼ 三、裂区试验的线性模型和期望均方 ◼ 四、再裂区设计的分析 ◼ 五、条区设计的分析

一、裂区试验结果统计分析示例 ■设有A和B两个试验因素，A因素为主处理，具a个水 平，B因素为副处理，具b个水平，设有个区组，则 该试验共得rab个观察值。其各项变异来源和相应的 自由度见表13.23

一、裂区试验结果统计分析示例 ◼ 设有A和B两个试验因素，A因素为主处理，具a个水 平，B因素为副处理，具b个水平，设有r个区组，则 该试验共得rab个观察值。其各项变异来源和相应的 自由度见表13.23

表13.23二裂式裂区试验自由度的分解 变异来源 DF 平方和 主区部分 区组 r-1 SSR-∑2/ab-c A a-1 SSA=ET2/rb-C 误差a (r-1)(a-1) SSE,=主区SS-SSR-SSA 主区总 变异 ra-l 主区SS 副区部分 B b-1 SSB =ETR/ra-C AXB (a-1)b-1) SS4B=处理SS-SS4SSB 误差b a(r-1)(b-1) SSE,=SS7-主区总SS-SS&-SSAB 总变异 rab-1 SSr=∑y2-C

变异来源 DF 平 方 和 主区部分 区组 r-1 A a-1 误差a (r-1)(a-1) 主区SS-SSR -SSA 主区总 变异 ra-1 主区SS 副区部分 B b-1 A×B (a-1)(b-1) SSAB=处理SS-SSA -SSB 误差b a(r-1)(b-1) SST -主区总SS-SSB -SSAB 总 变 异 rab-1 表13.23 二裂式裂区试验自由度的分解 SSR = Tr ab −C 2 SSA = TA rb − C 2 = Ea SSSSB = TB ra − C 2 = Eb SS SST =  y −C 2