南京农业大学：《生物统计与田间试验》课程教学资源（PPT课件）第十三章 多因素试验结果的统计分析

■作随机区组设计，设有个区组，则该试验共有rabc 个观察值，其各项变异来源及自由度的分解见表 13.15

◼ 作随机区组设计，设有r个区组，则该试验共有rabc 个观察值，其各项变异来源及自由度的分解见表 13.15

表13.15 三因素随机区组试验的平方和及自由度分解 变异来源 DF SS 区组 r-1 SSR=∑T2abc-C 处理 abc-1 SS,=∑Tcr-C A a-1 SS4=∑Trbc-C B b-1 SSa=∑TB2/rac-C c c-1 SSe=∑1Te2/rab-C AXB (a-1)b-1) SSAB=∑TB/rC-SSrSSB AXC (a-1)c-1) SS4c=∑Tic/rb-S4Sc BXC (b-1)(c-1) SSBc=∑Tic/r6Sg-SSc AXBXC (a-1)b-1)(c-1) SSABC-SS-SSA-SSB-SSC-SSAB-SSAC-SSEC 误差 (r-1)(abc-1) SS=SST-SS,-SSR 总变异 rabc-1 SSr=∑y2-C

表13.15 三因素随机区组试验的平方和及自由度分解 变异来源 DF SS 区 组 r-1 处 理 abc-1 A a-1 B b-1 C c-1 A×B (a-1)(b-1) -SSA -SSB A×C (a-1)(c-1) -SSA -SSC B×C (b-1)(c-1) -SSB -SSC A×B×C (a-1)(b-1)(c-1) SSABC=SSt -SSA -SSB -SSC -SSAB-SSAC-SSBC 误 差 (r-1)(abc-1) SSe=SST -SSt -SSR 总 变 异 rabc-1 SSR = Tr abc −C 2 SSt = TABC r −C 2 SSA = TA rbc −C 2 SSB = TB rac −C 2 SSC = TC rab−C 2 SSAB = TAB rc − C 2 SSAC = TAC rb −C 2 SSBC TBC ra 2 =  SST =  y − C 2

DF=DFA+DFR+DFC+DFAB+DFAC+DFRC+DFABC (13:4) SS,-SSA+SSB+SSC+SSAB+SSAC+SSEC+SSABC (13·5) ■（三)三因素试验的线性模型和期望均方 ■1.完全随机设计 ■三因素完全随机试验每一观察值y/的线性模型为： yu=u+A+B +Cx+(AB)y+(AC)ik+(BC)j+(ABC)uk+u (136)

◼ DFt =DFA+DFB+DFC+DFAB+DFAC+DFBC+DFABC (13·4) ◼ SSt =SSA+SSB+SSC+SSAB+SSAC+SSBC+SSABC (13·5) ◼ (三) 三因素试验的线性模型和期望均方 ◼ 1. 完全随机设计 ◼ 三因素完全随机试验每一观察值 yijkl 的线性模型为： (13·6) ijkl Ai Bj Ck AB i j AC i k BC j k ABC ijk ijkl y =  + + + +( ) +( ) +( ) +( ) + 

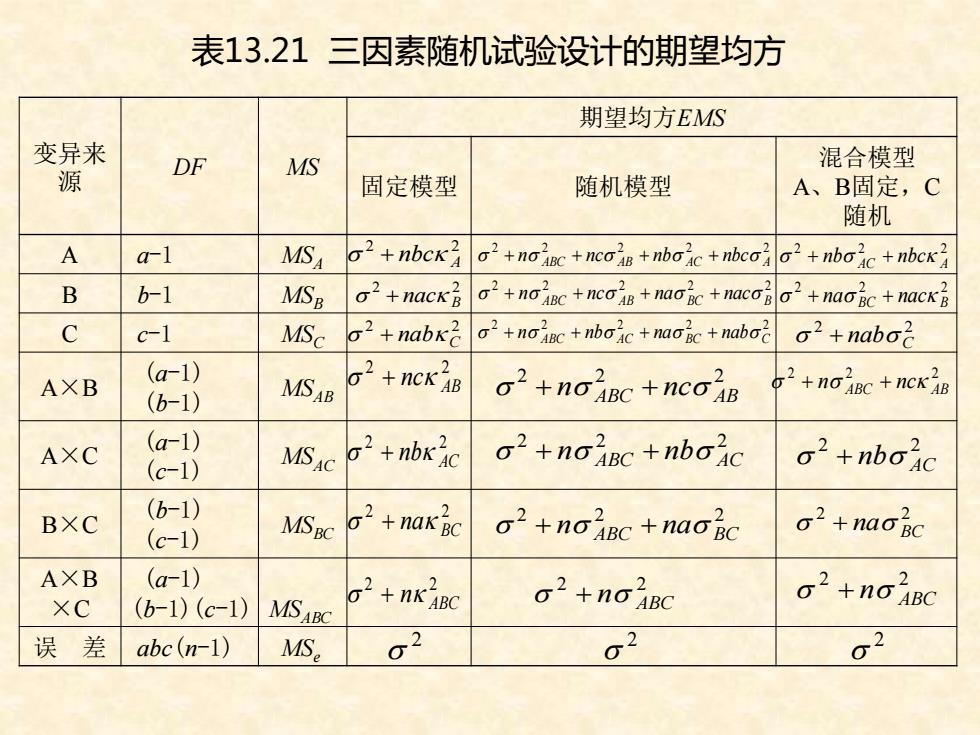
表13.21三因素随机试验设计的期望均方 期望均方EMS 变异来 DF MS 混合模型 源 固定模型 随机模型 A、B固定，C 随机 A a-1 MS o2+nbck G2+ngc+nca+nboic+nbco a2+nboc+nbc B b-1 MSB o2+nack o2+noinc +nco+nacic nac2+naoic+nack C c-1 MSc o2 nabke o2+nonc nbaic+naoic+naboc o2+naboc (a-1) AXB g2+ncK 、2 (6-1) MSAB 2+noanc+nen 2C+CK AB AXC (a-1) (c-1) MSAC g2 +nbkic o2+noanc +nboc o2+nboic BXC (b-1) (c-1) MSBC o2 nak ic 2 +noc+naobc a2+naoac AXB (a-1) ×C (b-1)(c-1)MS4Bc 2+HKBC G2+naBc 2+nonc 误差 abc(n-1) MSe 02 02 02

变异来 源 DF MS 期望均方EMS 固定模型 随机模型 混合模型 A、B固定，C 随机 A a-1 MSA B b-1 MSB C c-1 MSC A×B (a-1) (b-1) MSAB A×C (a-1) (c-1) MSAC B×C (b-1) (c-1) MSBC A×B ×C (a-1) (b-1)(c-1) MSABC 误 差 abc(n-1) MSe 表13.21 三因素随机试验设计的期望均方 2 2  + nbc A 2 2  + nac B 2 2  + nab C 2 2 AB  + nc 2 2 AC  + nb 2 2 BC  + na 2 2 ABC  + n 2  2  2  2 2 2 2 2 ABC AB AC A  + n + nc + nb + nbc 2 2 2 2 2 ABC AB BC B  + n + nc + na + nac 2 2 2 2 2 ABC AC BC C  + n + nb + na + nab 2 2 2  + n ABC + nc AB 2 2 2  + n ABC + nb AC 2 2 2  + n ABC + na BC 2 2  + n ABC 2 2 2 AC A  + nb + nbc 2 2 2 BC B  + na + nac 2 2  + nab C 2 2 2 ABC AB  + n + nc 2 2  + nb AC 2 2  + na BC 2 2  + n ABC

■2.随机区组设计 ·三因素随机区组试验每一观察值yk,的线性模型为： yjklm=u+B +Ak +B+Cm+(AB)+(AC)m+(BC)m+(ABC)klm +jkm (13·7) ·其中，代表区组效应，固定模型时有∑B,随机 模型时~B,(楳余参教参见三因素完全随机 设计的情形

◼ 2. 随机区组设计 ◼ 三因素随机区组试验每一观察值yjklm的线性模型为： ◼ 其中， 代表区组效应，固定模型时有 ，随机 模型时 ～ ，其余参数参见三因素完全随机 设计的情形。 jklm j Ak Bl Cm AB kl AC km BC l m ABC klm jklm y =  +  + + + +( ) +( ) +( ) +( ) +  (13·7)  j   j = 0  j (0， ) 2 N  