
·实际研究中0未知,以样本标准差S作为0的估计值 计算标准误: Sx=S/√n P29 例4.1在某地随机抽查成年男子140人,测得红细胞 数均数为4.77×102儿,标准差0.38×102/几,试计算 其抽样误差的大小: S=S1√n=0.38/V140=0.032 11
• 实际研究中σ未知,以样本标准差 未知,以样本标准差 未知,以样本标准差 未知,以样本标准差S作为σ的估计值 计算标准误: 例4.1 在某地随机抽查成年男子 在某地随机抽查成年男子 在某地随机抽查成年男子 在某地随机抽查成年男子140人,测得红细胞 人,测得红细胞 人,测得红细胞 人,测得红细胞 数均数为4.77×102 /L,标准差0.38 ×102 /L ,试计算 其抽样误差的大小 其抽样误差的大小 其抽样误差的大小 其抽样误差的大小: S S n X = / S = S / n = 0.38/ 140 = 0.032 X P29 11

二、样本均数的抽样分布持点 >各样本均数未必等于总体均数 >样本均数之问存在差异 >样本均数的分布很有规律,围绕着总体均 数左右基本对称,也服从正态分布 >样本均数的变异较原变量的变异大大缩小 0 40 0 150 0 50 均 9分心原今个 令分2 的 均数
二、样本均数的抽样分布特点 � 各样本均数未必等于总体均数 � 样本均数之间存在差异 � 样本均数的分布很有规律,围绕着总体均 数左右基本对称,也服从正态分布 � 样本均数的变异较原变量的变异大大缩小 0 50 100 150 200 250 300 350 400 450 3.71 3.92 4.12 4.33 4.54 4.74 4.95 5.15 5.36 5.57 5.77 5.98 6.19 均数 频数 0 50 100 150 200 250 300 350 400 450 3.71 3.92 4.12 4.33 4.54 4.74 4.95 5.15 5.36 5.57 5.77 5.98 6.19 均数 频数 0 50 100 150 200 250 300 350 400 450 3.71 3.92 4.12 4.33 4.54 4.74 4.95 5.15 5.36 5.57 5.77 5.98 6.19 均数 频数 12
中心极限定理: 当样本含量很大的情况下,无论原始测量变量服从 什么分布,F的抽样分布均近似正态。 抽样分布 抽样分布示意图 13
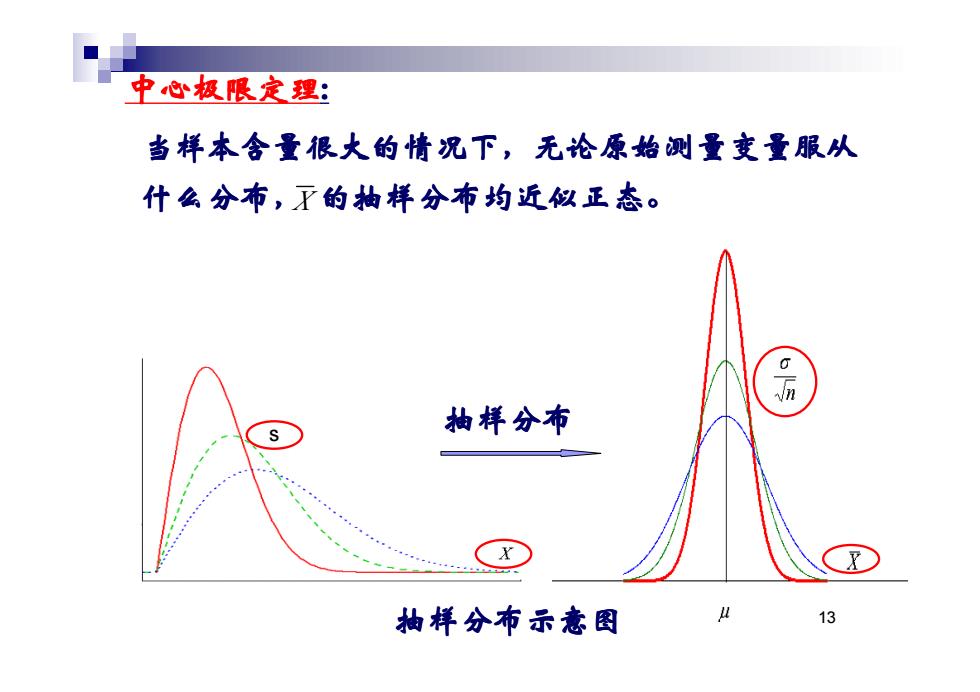
中心极限定理: 当样本含量很大的情况下,无论原始测量变量服从 当样本含量很大的情况下,无论原始测量变量服从 当样本含量很大的情况下,无论原始测量变量服从 当样本含量很大的情况下,无论原始测量变量服从 什么分布,X 的抽样分布均近似正态。 的抽样分布均近似正态。 的抽样分布均近似正态。 的抽样分布均近似正态。 抽样分布 抽样分布示意图 抽样分布示意图 抽样分布示意图 抽样分布示意图 s 13

标准误的用途 ■衡量抽样误差的火小,标准误越小,样本均数与 总体均数越接近,样本均数的可信度越高 ■结合标准正态分布与t分布曲线下面积分布规律, 估计总体均数的可信区问 ■用于假设检验 ■标准差与标准误的区别和联象? 14
标准误的用途 � 衡量抽样误差的大小 抽样误差的大小 抽样误差的大小 抽样误差的大小,标准误越小,样本均数与 ,标准误越小,样本均数与 ,标准误越小,样本均数与 ,标准误越小,样本均数与 总体均数越接近,样本均数的可信度越高 总体均数越接近,样本均数的可信度越高 总体均数越接近,样本均数的可信度越高 总体均数越接近,样本均数的可信度越高 � 结合标准正态分布与 结合标准正态分布与 结合标准正态分布与 结合标准正态分布与t分布曲线下面积分布规律, 分布曲线下面积分布规律, 分布曲线下面积分布规律, 分布曲线下面积分布规律, 估计总体均数的 估计总体均数的 估计总体均数的 估计总体均数的可信区间 � 用于假设检验 � 标准差与标准误的区别和联系? 标准差与标准误的区别和联系? 标准差与标准误的区别和联系? 标准差与标准误的区别和联系? 14

t分布 >从正态总体N(山,G2)中随机抽取样本会 量为n的样本,获得的样本均数的分布 服从正态分布N(4,G是)。 >同样可以对呈正态分布的x进行u变换 x-八 M= 15
�从正态总体N(μ,σ2 )中随机抽取样本含 量为n的样本,获得的样本均数的分布 服从正态分布 N(μ, ) 。 �同样可以对呈正态分布的 进行u变换 2 σ x t 分布 x x x u σ − µ = 15