1 x2 sin 例7求im x x->0 sinx 0 解这个问题是属于 型未定式,但分子分母分别 1 1 2xsi 1-cos 求导后得 X x COSx 此式振荡无极限,故洛必达法则失效,不能使用。 但原极限是存在的,可用下法求得 2 sin- lim x=lim- x>0 sinx x→0S1nx 前页后页结束
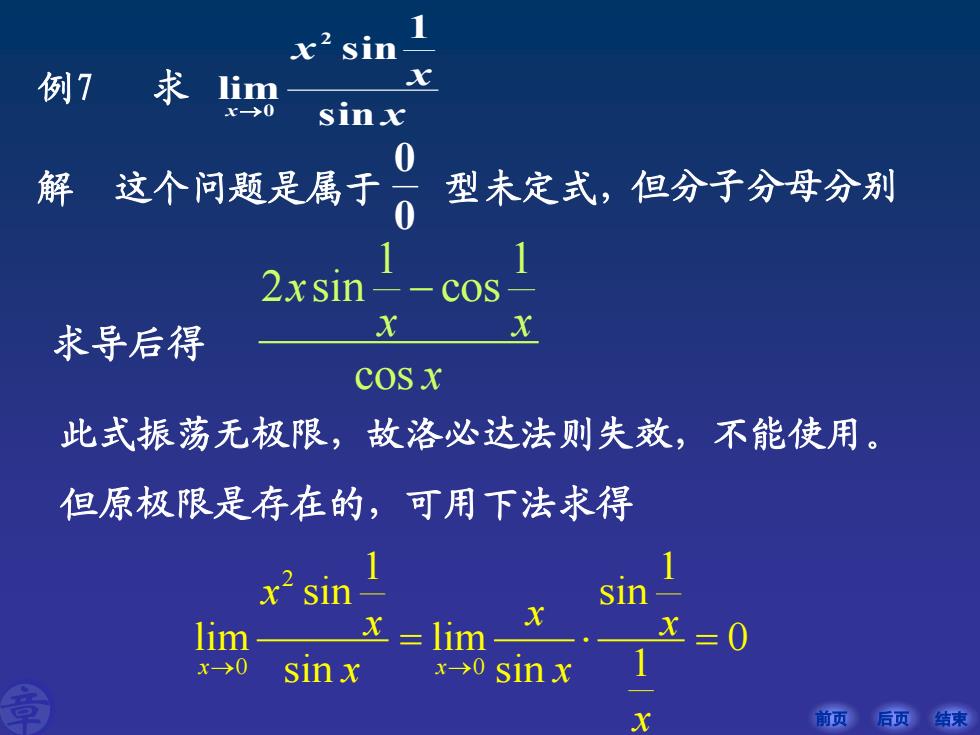
前页 后页 结束 例7 求 x x x x sin 1 sin lim 2 →0 解 这个问题是属于 0 0 型未定式, 2 0 0 1 1 sin sin lim lim 0 x x sin sin 1 x x x x x x x → → = = 但分子分母分别 1 1 2 sin cos cos x x x x − 求导后得 此式振荡无极限,故洛必达法则失效,不能使用。 但原极限是存在的,可用下法求得
3.其它型不定式 未定式除 0 和 型外,还有 0 00 0.00 型、 00一00 型、 0° 型、 000 型、 1 型、 等五种类型。 前页后页结束
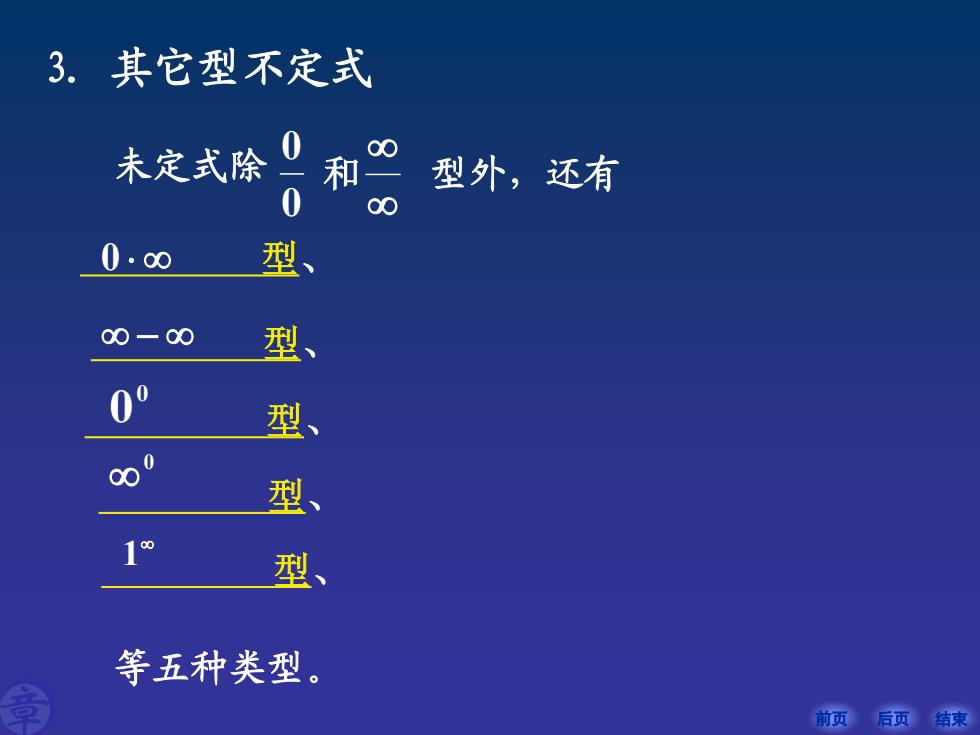
前页 后页 结束 3.其它型不定式 未定式除 0 0 和 型外,还有 1 0 0 0 0 − 型、 型、 等五种类型。 型、 型、 型
0.0型: 变为四=型或者0型 00 00 0 00 例8 求Iimx3nx x→0t 解 lim x3Inx=lim Inx 00 (型) x0 x→0 1 00 X 1 lim x→0t 3 lim lim- x0*-3xx0* 3 =0 前页后页结束
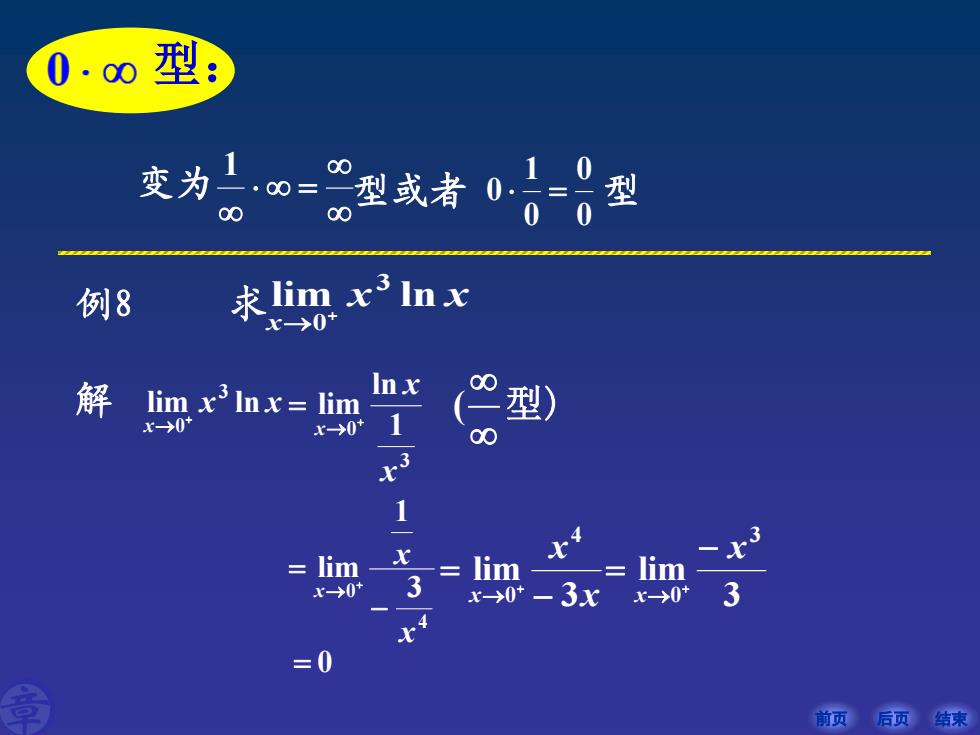
前页 后页 结束 型或者 型 型: = 1 0 0 0 1 0 = ( 型) 变为 x x x lim ln 3 0 → + 3 0 1 ln lim x x x→ + = 4 0 3 1 lim x x x − = → + x x x 3 lim 4 0 − = → + 3 lim 3 0 x x − = → + x x x lim ln 3 0 例8 求 → + 解 = 0
00 一00型: 0 通分相减变为 -0 型 例9求im( 00-00 x-1 Inx 型) lim( 1 -)=im xInx-x-1 解 x-1 Inx x(x-1)Inx 型) Inx lim- lim- Inx+1-1 x→1 1 1-~+Inx x-1x-1 (8 型) lim- 1 x→1 前页后页结束
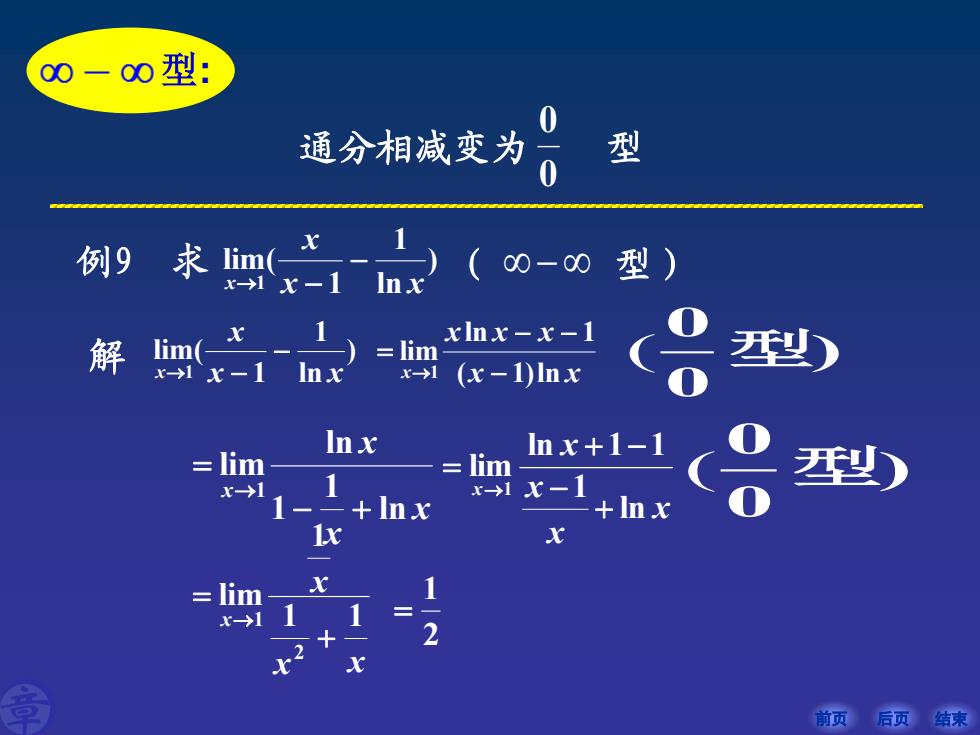
前页 后页 结束 型: 通分相减变为 型 0 0 例9 求 ) ln 1 1 lim( 1 x x x x − → − ( − 型) 解 ) ln 1 1 lim( 1 x x x x − → − x x x x x x ( 1)ln ln 1 lim 1 − − − = → ( 0 ) 0 型 x x x x x ln 1 ln 1 1 lim 1 + − + − = → x x x x ln 1 1 ln lim 1 − + = → x x x x 1 1 1 lim 2 1 + = → 2 1 = ( 0 ) 0 型

1000o00型未定式: 由于它们是来源于幂指函数((x)o的极限 因此通常可用取对数的方法或利用((x)》F田=e8r/ ●● 即可化为00型未定式,再化为二型或型求解。 0 oo 例10求1imx*(0°型 x-→0t lim xInx 解 limx=lim exinx =e x→0 x→0t 1 x→0 =了==m)=0 lim xInx lim Inx x→0* 2 所以imxx=e°=1 x→0 前页 后页结束
前页 后页 结束 1 0 0 0 型未定式: 由于它们是来源于幂指函数 ( f (x)) g( x) 的极限 因此通常可用取对数的方法或利用 ( ) ( ) ( ) g x f x g( x)ln f ( x) = e 0 0 即可化为 0 型未定式,再化为 型或 型求解。 例10 求 x x x → + 0 lim 0 (0 ) 型 x x x x x x x x x e e lim l n l n 0 0 0 lim lim → + + + = = → → x x x lim ln 0 → + x x x 1 ln lim 0 → + = 2 0 1 1 lim x x x − = → + lim ( ) 0 0 = − = → + x x lim 1 0 0 = = → + x e x x 解 所以