
第2章导数与微分 1.1导数的概念 1.2导数的运算 1.3微分 结速
第2章 导数与微分 1.1 导数的概念 1.2 导数的运算 1.3 微分 结束
2.1导数的概念 2.1.1引出导数概念的实例 例1平面曲线的切线斜率 y=f(x) 曲线y=的圍像如图所示, 在曲线上任取两点M(x,) △X 和N(x,+△x,+△y)作割线 Xo x0+△x X 公W割线的斜率为 =tan =△y=(x,+△)-fx) △K △x 前页后页结束
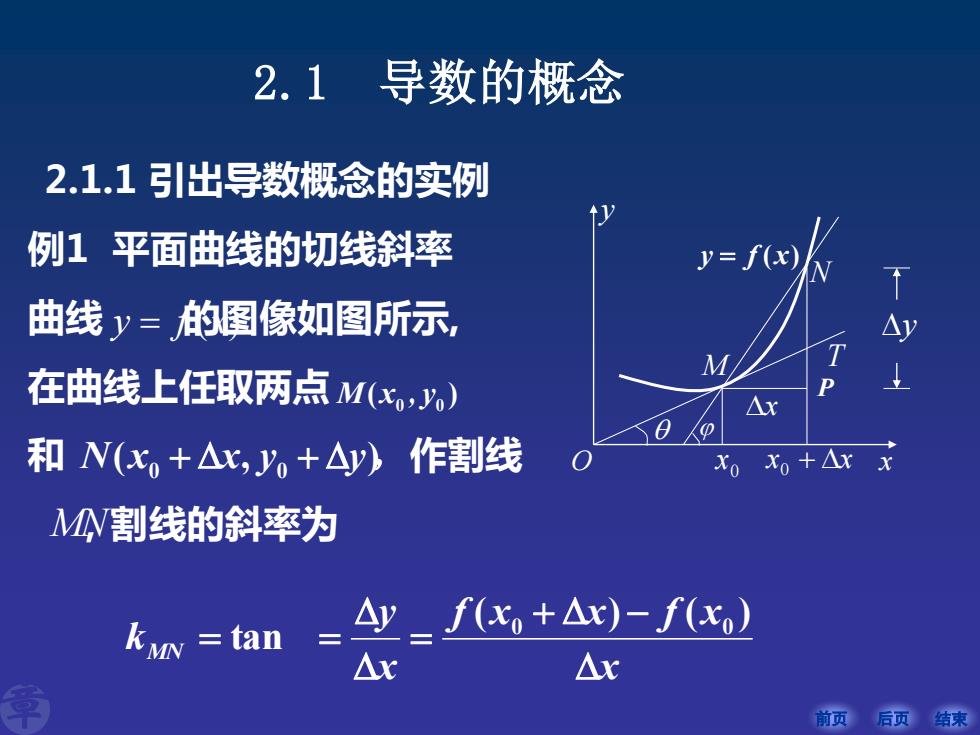
前页 后页 结束 2.1.1 引出导数概念的实例 例1 平面曲线的切线斜率 曲线 的图像如图所示, 在曲线上任取两点 和 ,作割线 ,割线的斜率为 y = f (x) 0 0 M x , y ( ) ( , ) 0 0 N x + x y + y x f x x f x x y k MN + − = = = ( ) ( ) tan 0 0 MN 2.1 导数的概念 y O x y f x = ( ) M N T x 0 x x + x 0 y P

这里为割线MW的倾角,设是切线MT的倾角, 当△x时0点N沿曲线趋于点M。若上式的 极限存在,记为k,则此极限值就是所求切线 MT的斜率,即 k tan=lim tan y=f(x) △x→0 lim y △ Ax→0△X △X lim f(x,+△x)-f(x) △x→0 △x Xo xg+△x 前页后页结束
前页 后页 结束 这里 为割线MN的倾角,设 是切线MT的倾角, 当 时,点N沿曲线趋于点M。若上式的 极限存在,记为k,则此极限值k就是所求切线 MT的斜率,即 x f x x f x x y k x x x + − = = = = → → → ( ) ( ) lim lim tan lim tan 0 0 0 0 0 θ x → 0 y O x y f x = ( ) M N T x 0 x x + x 0 y P

例2产品总成本的变化率 设某产品的总成本C是产量Q的函数,即C=C(Q),当产 量Q从2,变到2,+△2时,总成本相应地改变量为 △C=C(2,+△Q)-C(2) 当产量从2,变到2,+△2时,总成本的平均变化率 △CC(2+△2)-C(2) △Q △Q 当△Q趋向于0时,如果极限 △C lim lim C(2,+△2)-C(2) △2→0 △Q 存在,则称此极限是产量为Q,时总成本的变化率。 前页后页结束
前页 后页 结束 当 趋向于0时,如果极限 设某产品的总成本C是产量Q的函数,即C=C(Q ),当产 量Q 从 变到 时,总成本相应地改变量为 当产量从 变到 时,总成本的平均变化率 Q0 Q Q 0 + 0 0 = + − C C Q Q C Q ( ) ( ) Q0 Q Q 0 + 0 0 C C Q Q C Q ( ) ( ) Q Q + − = 0 0 0 0 ( ) ( ) lim lim Q Q C C Q Q C Q → → Q Q + − = 存在,则称此极限是产量为 Q0 时总成本的变化率。 →Q 0 例2 产品总成本的变化率

2.1.2导数的概念 定义设y=fx)在点x的某邻域内有定义,xo+△x 属于该邻域,记△y=f(x,+△x)-f(x), 若 f(x+△x)-f(c,) lim Ay lim △x→0△X△x-→0 △x 存在,则称其极限值为y=fx)在点x。处的导数,记为 ,)减r或或 dx x=x x 或 f)=lim g=im/&+△x)-fx △x→0△x △r→0 △x 前页后页结束
前页 后页 结束 定义 设y=f(x)在点x0的某邻域内有定义, 属于该邻域,记 若 存在,则称其极限值为y = f (x)在点x0 处的导数,记为 x + x 0 ( ) ( ), 0 x0 y = f x + x − f = → x y x 0 lim x f x x f x x + − → ( ) ( ) lim 0 0 0 | . d d | , d d ( ) | , 0 0 0 0 x x x x x x x f x y f' x y' 或 = 或 = 或 = . ( ) ( ) ( ) lim lim 0 0 0 0 0 x f x x f x x y f' x x x + − = = → → 或 2.1.2 导数的概念