
18 第一章数学基础 12=p1<5×10 ■ D 表1.1对于不同的力值列举了当p·近似p到4位有效数字时|p-p·|的最小上界,记为 maxp-p·|,由此表明了有效数字的连续性质。 表1.1 p 0.1 0.5 100 10005000999010000 max|p-p·| 0.000050.000250.05 0.5 2.54.995 5 回到数的机器表示,可知数y的浮点表示式(y)具有相对误差 y-fi(y) y 如果对于 y=0.d1d2.dd+1.×10 的机器表示式使用截断法保留k位十进制数字,则 y-y=|0.dd,.dd.×10-0.d,d4.dx10 0.d1d2.×10" x10 因为d,≠0,所以分母的最小值是0.1。分子以1为上界。从而有 y=2×10=10 类似地,当使用k位四舍五入运算时相对误差界是0.5×10+。(见第24题。) 注意到使用k位算术的相对误差的界与被表示的数无关。这个结果是由机器数在实数轴 上的分布方式而决定的。由于机器数表示的指数形式,为了表示[0.1,1],[1,10]和[10,100]中 的每一个区间,因而使用同样数目的十进制机器数。实际上,在机器的有效数范围内,位于区间 [10°,10+]内的十进制机器数的数目对于一切整数n是一个常数。 除了数的不精确表示外,由计算机所完成的算术运算也是不精确的。算术运算涉及对二进 制数进行各种移位运算或逻辑操作。因为这些操作的实际机制与数的表示法无关,所以可以对 计算机算术来设计我们自己的近似算法。虽然计算机算术不能反映确切的情况,但是它足以解 释所发生的问题。(对于实际涉及的操作的解释,建议读者参阅有关技术型导向的计算机科学教 材,如[Ma],Computer System Architecture) 假设给定实数x和y的浮点表示为(x)和(y),又假定符号田、⊙、☒和Θ分别代表机器 加、减、乘和除的操作。可以假定有限位的算术运算为 x⊕y=f(f(x)+f(y),x⑧y=f(f(x)×f(y) xey=fl(fl(x)-fl(y)),xey=fl(fl(x)fl(y))
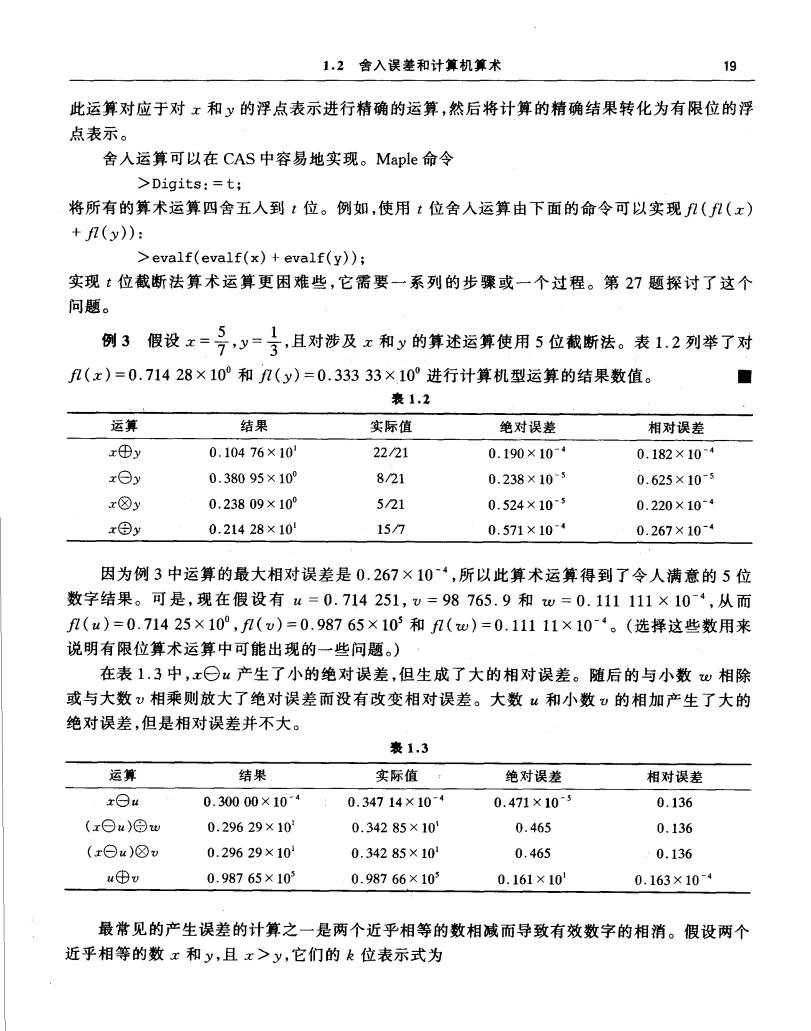
1.2舍入误差和计算机算术 19 此运算对应于对x和y的浮点表示进行精确的运算,然后将计算的精确结果转化为有限位的浮 点表示。 舍人运算可以在CAS中容易地实现。Maple命令 >Digits:=t; 将所有的算术运算四舍五人到t位。例如,使用t位舍人运算由下面的命令可以实现f几((x) +f(y): >evalf(evalf(x)+evalf(y)); 实现t位截断法算术运算更困难些,它需要一系列的步骤或一个过程。第27题探讨了这个 问题。 例3假设x=号,y=号,且对涉及x和y的算述运算使用5位截断法。表1.2列举了对 f(x)=0.71428×10°和(y)=0.33333×10°进行计算机型运算的结果数值。 ■ 表1.2 运算 结果 实际值 绝对误差 相对误差 x⊕y 0.10476×10 2221 0.190×10 0.182×104 rey 0.38095×10° 821 0.238×105 0.625×10-5 x⑧y 0.23809×10° 521 0.524×103 0.220×104 xΘy 0.21428×10 15/7 0.571×104 0.267×10-4 因为例3中运算的最大相对误差是0.267×10‘,所以此算术运算得到了令人满意的5位 数字结果。可是,现在假设有u=0.714251,v=98765.9和w=0.111111×104,从而 (u)=0.71425×10°,f(v)=0.98765×103和f(w)=0.11111×10‘。(选择这些数用来 说明有限位算术运算中可能出现的一些问题。) 在表1.3中,x⊙“产生了小的绝对误差,但生成了大的相对误差。随后的与小数w相除 或与大数v相乘则放大了绝对误差而没有改变相对误差。大数“和小数,的相加产生了大的 绝对误差,但是相对误差并不大。 表1.3 运算 结果 实际值 绝对误差 相对误差 rOu 0.30000×104 0.34714×104 0.471×105 0.136 (xOu)⊙w 0.29629×10 0.34285×10 0.465 0.136 (xOu)⑧ 0.29629×10 0.34285×10 0.465 0.136 u⊕v 0.98765×10 0.98766×10 0.161×10 0.163×10-4 最常见的产生误差的计算之一是两个近乎相等的数相减而导致有效数字的相消。假设两个 近乎相等的数x和y,且x>y,它们的k位表示式为

名 第一章数学基础 f(x)=0.d1d2.dap+1ap+2.a4×10 花 f1(y)=0.d1d2.d月。iB。2.A×10" x-y的浮点形式是 f(f(x)-f(y)=0.a+1a+2.a.×10- 其中 0.0+10+2.可=0.ap+1ap+2.a4-0.月+1月+2.月 用于表示x一y的浮点数至多有k-p位有效数字。可是,在大多数计算装置中,x-y被分配k 位,其中最后的p位或者是零或者是任意分配的值。涉及x一y的任何进一步计算仍然存在仅 有k一力位有效数字的问题,这是因为计算链和其最弱部分的问题一样不精确。 如果有限位的表示或计算产生了误差,则当用一个小量值的数去除(或等价地,用一个大量 值的数相乘)时会使误差进一步加大。例如,假设数x具有有限位的近似z+6,这里误差8是由 表示法或以前的计算所引入的。假定现在用e=10"去除,这里n>0,则 名≈n28=(e+a)×10 这样,在这个近似计算中的绝对误差|6×10是原来的绝对误差|6的10°倍。 例4设p=0.54617,q=0.54601.7=p-q的精确值是r=0.00016。假定减法用4位 算术运算来完成。将p和q四舍五人到4位数分别得到p·=0.5462,q·=0.5460。 r·=p·-q'=0.0002是r的4位近似值。因为 1r-1_10.00016=0.0002=0.25 T0.00016 所以结果仅有一位有效数字,而p”和9”分别精确到4位和5位有效数字。 如果使用截断法来获得4位数字,则p,q和r的4位近似数为p°=0.5461,g°=0.5460 和r·=p·-q=0.0001。由此得到 1r-r1_10.00016-0.0001=0.375 0.00016 结果仅有一位有效数字的精度。 ■ 由于舍入误差而产生的精度损失往往可通过将问题中的公式重新变形来避免,正如下面的 例子所示。 例5根据二次公式所述,当a≠0时,方程a.x2+bx+c=0的根为 x1=二b+y8-4ac和,=二b-6-4a 2a (1.1) 使用4位四舍五人运算,考虑将公式应用到方程x2+62.10x+1=0,可得到其根近似为 x1=-0.01610723和x2=-62.08390

1.2舍入误差和计算机算术 21 在这个方程中,b2比4αc要大得多,因而计算x1的公式中的分子涉及两个近乎相等的数的 相减。因为 √62-4ac=√(62.10)2-(4.000)(1.000)(1.000) =√3856-4.000=√3852 =62.06 则有 (x)=-62.10+62.06 2.000 = -0.04000=-0.02000 2.000 这是x1=-0.01611的一个不好的近似值,具有较大的相对误差 1-0.01611+0.02000≈2.4×10 T-0.01611T 另一方面,对x2的计算涉及到两个近乎相等的数-b和-√6-4c的相加。这没有引发任何 问题,因为 n(x2)=-62,10-62.06= 2.000 -124.2=-62.10 2.000 具有较小的相对误差 1-62.08+62.10l≈3.2×10· -62.08 为了得到x,的更精确的4位舍入近似值,通过有理化分子将二次公式的形式变为: x1=-6+yB2-4ac|-6-VB-4ac 2a -b-√62-4ac b2-(b2-4ac) “2a(-b-4ac】 从而进一步化简为二次公式的替代式 -2c x1 (1.2) b+√6-4ac 使用式(1.2)得到 -2.000 -2.000=-0.01610 n(x)=62.i0+62.06124:2 上式具有较小的相对误差6.2×10“。 ◆ 有理化方法也可用于给出下面计算x2的二次公式的替代式 -2c -6-√D-4ac 3

22 第一章数学基础 如果b是负数,就使用这个形式。可是,在例5中错误地使用x2的这个公式不仅会导致两个近 乎相等的数的相减,而且还导致这个小的相减结果被用作除数。由此叠加产生的不精确值为 -2c -2.000 (x)6-√6-4ac62.10-62.06 -2.000 0.0400=-50.0 它具有较大的相对误差1.9×101。 由舍人误差造成的精度损失也可通过重新安排计算来减小,正如下例所示。 例6利用3位算术运算求f(x)=x3-6.1x2+3.2x+1.5在x=4.71处的值。 表1.4给出了计算的中间结果。仔细检查这些结果以确定有关有限位算术运算的概念是正 确的。注意到用截断法所得到的3位数值仅保留前3位数字而不涉及到四舍五入运算,这与使 用舍人法所得到的3位数值大不相同。 表1.4 x 6.1x2 3.2x 精确值 4.71 22.1841 104.487111 135.32301 15.072 3位数值(截断法) 4.71 22.1 104 134 15.0 3位数值(舍入法) 4.71 22.2 105 135 15.1 精确值:f(4.71)=104.487111-135.32301+15.072+1.5 =-14.263899 3位数值(截断法):f(4.71)=(104-134)+15.0)+1.5=-13.5 3位数值(舍入法):f(4.71)=(105-135)+15.1)+1.5=-13.4 上述3位数值方法的相对误差分别是 -14.263899+13.5≈0.05,截断法 -14.263899 1-14.263899+13.4≈0.06,舍人法 -14.263899 作为另一种办法,用嵌套的方式可将f(x)写为 f(x)=x3-6.1x2+3.2x+1.5 =(x-6.1)x+3.2)x+1.5 从而得到 3位数值(截断法):f(4.71)=(4.71-6.1)4.71+3.2)4.71+1.5=-14.2 由舍入法得到的3位数值答案为-14.3。新的相对误差为