
0-(g,og,-2&+2· -2 gn 人e1 对每个4,1≤“≤,我们得到一个线性方程组: 0 ° 因为det饥g≠0,所以对所有1和4只有平凡解:,04一0。它 在整个V上成立.所以Cauchy-Riemann微分方程组满足且g1 是全纯的。 定理75。设BCC是个区域,g一(g1,··,8)全纯且在 B中是一对一的.则在整个B上,M。≠0.·, 这个定理在实的情况是不成立的,例如y=x是一对一的, 但其导数y=3x2在原点为0. 这里我们将不给出定理7.5的证明.(在R.Narasimhan所 "Several Complex Variables",Chicago Lectures in Mathema- tics,1971的第五章的定理5中,能找到这个证明). 定理7.6.设BCC是一个区域,g:B,→C是一对一且全 纯的.则B,■g(B)也是一个开集合且g:B,→B,是全纯的. 证明: 1.设EB,则存在一个0EB:满足g(0)=.从定理 7.5知,在B,上Mg中0,因而有开邻域U(0)CB1,V(o)CC,使 得g:U→V是双全纯的.但另一方面,V一g(U)Cg(B)B: 即是一个内点. 2.从(1),对每个∈B,有一个开邻域V(m)二B,使得 g|V是全纯的。 0 ·.34·

第二章全纯域 51.连续性定理 在本节和下一节中,我们将系统地讨论全纯函数的解析延拓 问题。 设P={∈C:l<1}是单位多圆柱,9i,·,9,0<9< 1,1≤y≤n是实数.则对2≤a≤n我们定义:D.={aEP: Il≤91且g≤I8al<1},D=UD.且 从2 H=P-D=∩(P-D). 4边2 则 H-{&∈P:8>9或|za|<9u,2≤a≤m} 、={aR:a<lzl}U{a∈P:z<9,2≤u≤n以. (P,H)称为一个“在C中的Euclid Hartogs图”.H是一个正常 Reinhardt域.h=P是它的完全包. 定义1.1.·设(P,H)是C中的一个Euclid Hartogs图,g= (g1,·,gn):P→C是一个双全纯映射,令户=g(P),立=g(H). 则(产,)称为一个一般的Hartogs图. 我们对n一3直观地说明这个概念。Euclid Hartogs图在绝 对空间中如图6所示,以后在C”中我们将采用下面的符号表示。 (实际情况要复杂得多.) 定理1.1.`设(户,)是C中一个一般Hartogs图,f在拉 中全纯。则恰有P上的一个全纯函数,满足F引狂=无, 证明:设(P,)=(g(P),g(H),g:P→C是双全纯 的.则和g在H中全纯,且由第一章定理5.5.在P上恰有一个金 和5
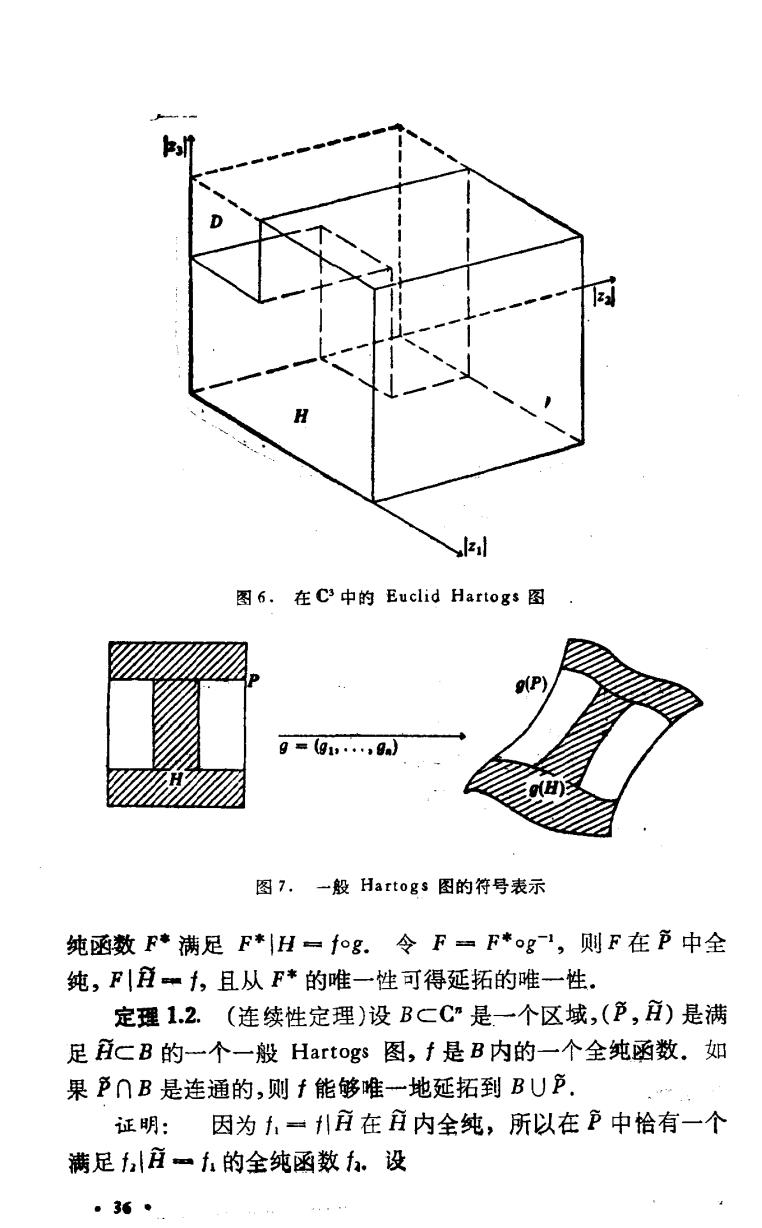
l 图6.在C3中的Euclid Hartogs图 9=(g1…,9} 图7,一般Hartogs图的符号表示 纯函数F*满足F*|H=f和g.令F=F*og1,则F在单中全 纯,F|丑千,且从F*的唯一性可得延拓的唯一性。 定理12.(连续性定理)设BCC”是一个区域,(P,a)是满 足HCB的一个一般Hartogs图,f是B内的一个全纯函数.如 果P∩B是连通的,则f能够唯一地延拓到BUP. 证明:因为,升应在应内全纯,所以在P中拾有一个 满足f庄=f的全纯函数币.设 ·36·

() 图8,连续性定理的说明 F(8)= f(8),a∈B, f(8),∈. 因为B∩P是一个域且刊应=庄,由此可知(从恒等定理)F是 BU产上的一个完全确定的全纯函数.显然FB■千,延拓的唯 一性是植等定理的一个进一步的推论, 0 连续性定理是所有进一步研究的基础。 定理13.设n≥2,P={:lz<1}是单位多圆柱,0≤ 8<1,y=1,…,n,P。={:z引≤,对所有}且G=P- 严·则G上每一个全纯函数都能够唯一地开拓为P上的一个全 纯函数. 证明: 1.显然,G是一个区域.如果=(”,·,),1▣1,2 给定,则点r(),r()也位于G中。对于11,2,我们能够在 环面上连接与r(x).定义p:1→C如下:p()m((e), ,4()),其中z)=|z41十t(max(z0,|一41), 1=1,2,”=1,…,.显然1(≥1之r8,”=1,…, n,因此,p()∈G,t∈1,1=1,2.设 p(2 00≤ p()= p(2-2),2≤1≤1, ·7·
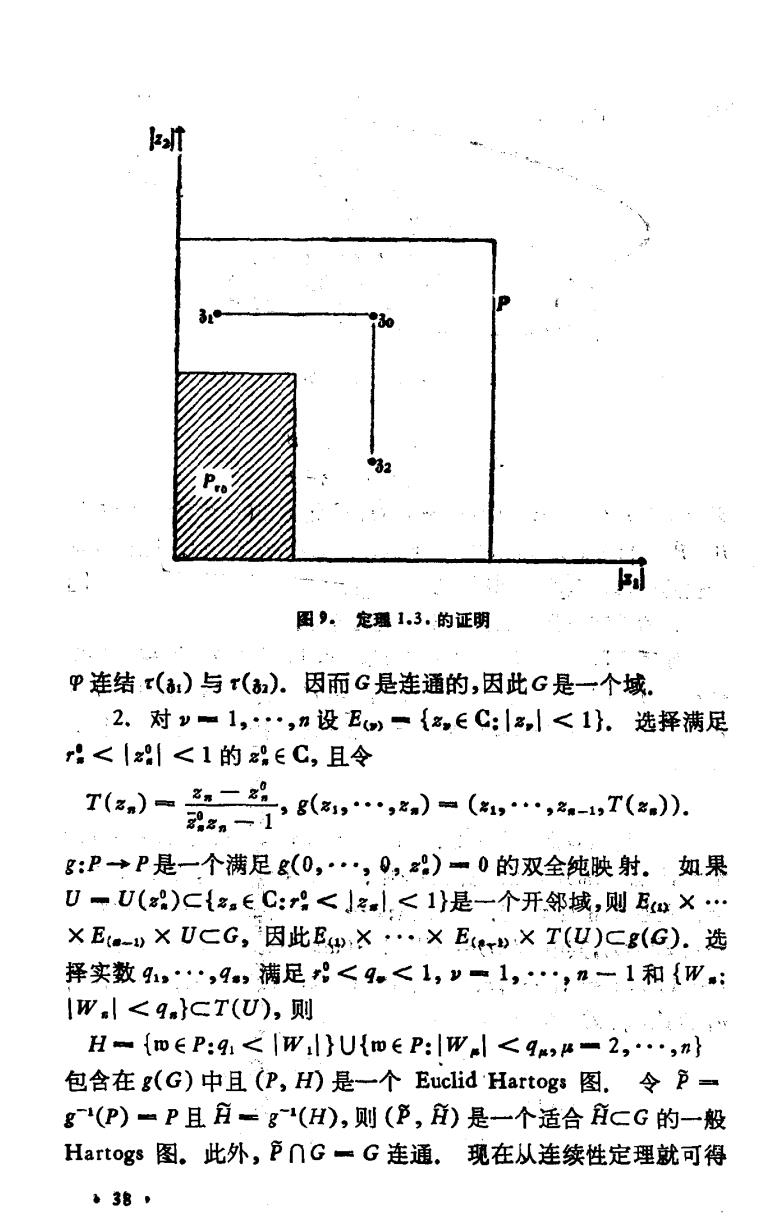
图9。定理1.3.的证明 P连结t()与t().因而G是连通的,因此G是一个域: 2、对v=1,…,n设E一{a∈C:|名,<1}.选择满足 r:<||<1的∈C,且令 T(a)=二2,g(,…,)=(,,-1,T(). zn一1 g:P→P是一个满足g(0,·,0,.)■0的双全纯映射。:如果 U一U()c{.∈C::<小l,<1}是一个开邻域,则耳m×… ×E-w×UCG,因此E…×Erw×T(U)Cg(G).选 择实数9,…,9,满足8<4。<1,”一1,…,n一1和{W IWl<9}CT(U八,则 H={o∈P:9<IWl}U{w∈P:lWl<9,4-2,·,n} 包含在g(G)中且(P,H)是一个Euclid Hartogs图.令P= g(P)=P且月=g(H),则(P,)是一个适合CG的一般 Hartogs图。此外,P∩G=G连通.现在从连续性定理就可得 38