中国地质大学（武汉）：《数字信号处理》课程教学资源（课件讲稿）第三章 离散傅里叶变换 Discrete Fourier Transform（DFT）

DFT与序列的DTFT和z变换的关系： X(e)=x(n)e N-I Xe)=Σxm)e” n=0 n=0 Xk)=Σx(mWg=Xe) N- n=0 =X(e) 2 xn)的N点DFT是 x(n)的z变换在单位圆上的N点等间隔抽样； x(n)的DTFT在区间[O,2]上的N点等间隔抽 样

x(n)的N点DFT是 x(n)的z变换在单位圆上的N点等间隔抽样； DFT z 与序列的DTFT和 变换的关系：1 0 ( ) ( ) N n n X z x n z      1 0 ( ) ( ) N nk N n X k x n W     1 0 ( ) ( ) N j j n n X e x n e        2 ( ) j k N X e     x(n)的DTFT在区间[0，2π]上的N点等间隔抽 样。 ( ) 2 j k k N N z W e X z     

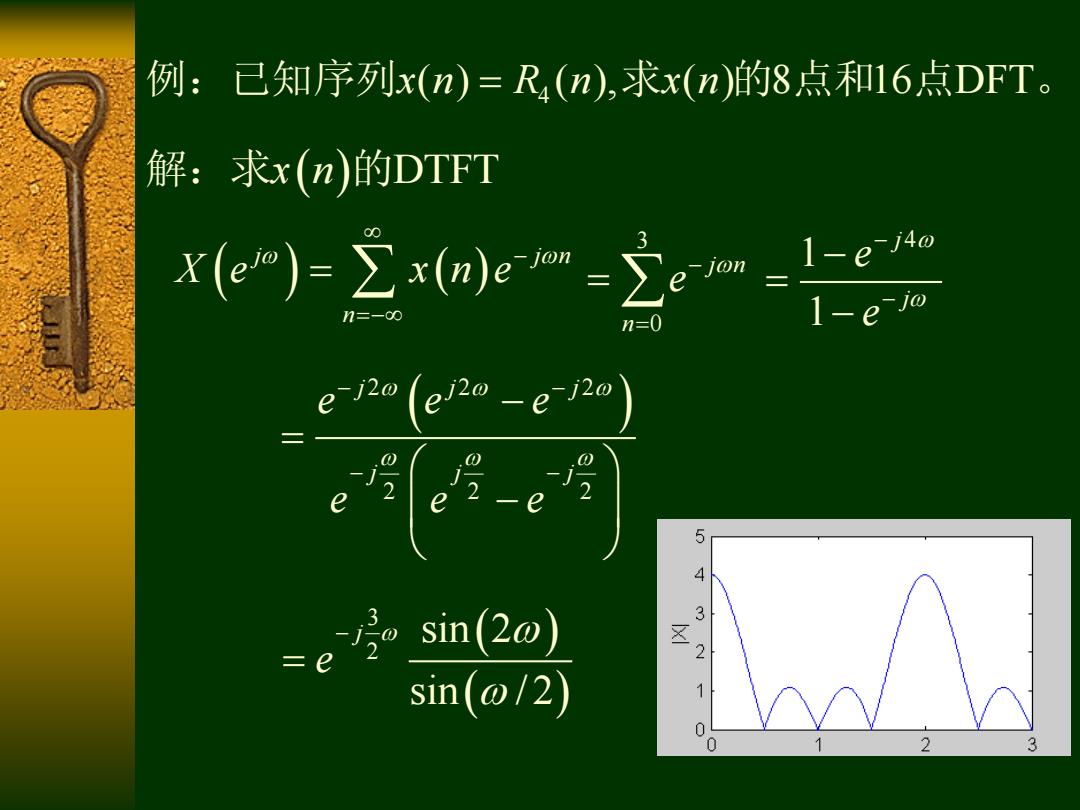
例：已知序列x(n)=R(n),求x(n)的8点和16点DFT。 解：求x(n)的DTFT e）主em-立- n= 1-e-jo e12o(e2-e-120 54 =e sin(20) 3 2 sin(@/2) 1 0 2 3

4 例：已知序列 求 的 点和 点 。 x n R n x n ( ) ( ), ( ) 8 16 DFT  解：求 的 x n  DTFT     j j n n X e x n e          2 2 2 2 2 2 j j j j j j e e e e e e                        3 2 sin 2 sin / 2 j e      3 0 j n n e      4 1 1 j j e e       

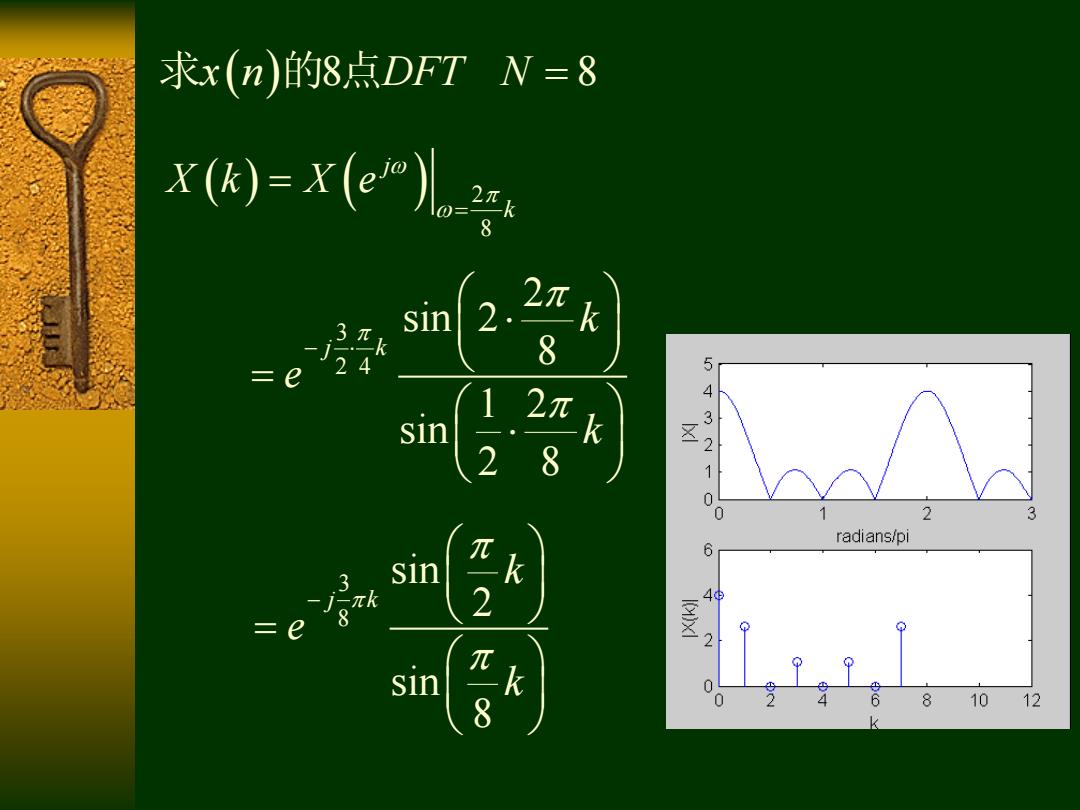
求x(n)的8点DFTN=8 X(k)=x(e儿 2 27 k 8 12π sin 28 54321 0 2 radians/pi 6 e i sin 2 4φ 2 π sin 8 0 81012

求 的 点 x n DFT N   8 8      2 8 j k X k X e     3 2 4 2 sin 2 8 1 2 sin 2 8 j k k e k                     3 8 sin 2 sin 8 j k k e k                 

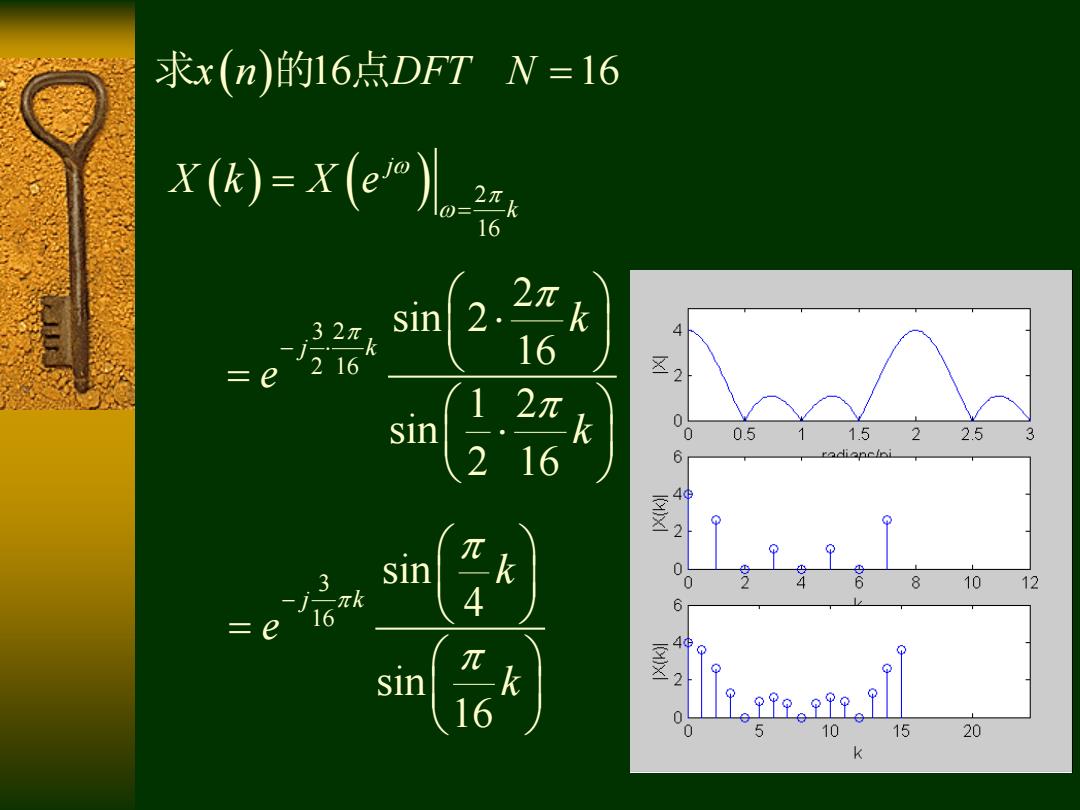
求x(n)的16点DFTN=16 x(k)=x(e”儿 2. sin 4 =e 216 16 2 1 2π sin k 0 0 0.5 1522.5 216 6 radianclni 2 sin 0 8 10 12 4 6 =e 49 sin 2 16 0 0 5 10 15 20

求 的 点 x n DFT N   16 16      2 16 j k X k X e     3 2 2 16 2 sin 2 16 1 2 sin 2 16 j k k e k                     3 16 sin 4 sin 16 j k k e k                 

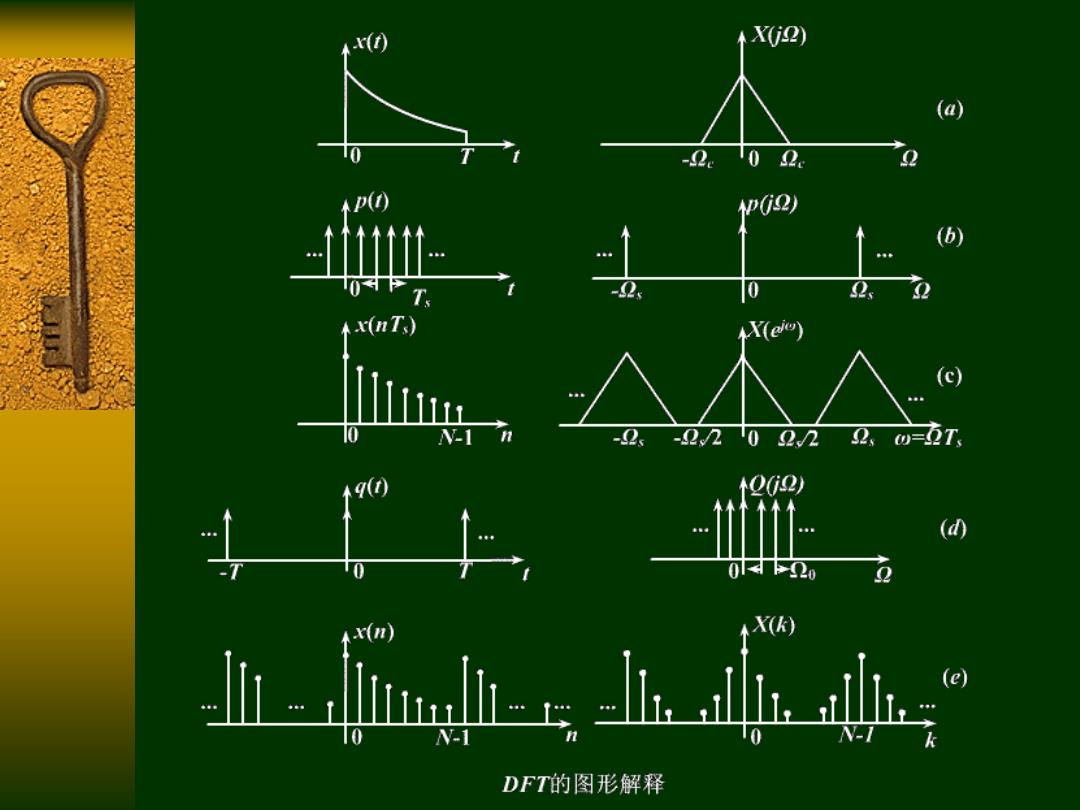
x() X(i2) (a) -2102x PGQ) (b) 0 2 Ax(nT) X(e) (c) N-I -2、-2,20222,w=5T o(2) (0 020 X(k) I mds 1 tt" DFT的图形解释