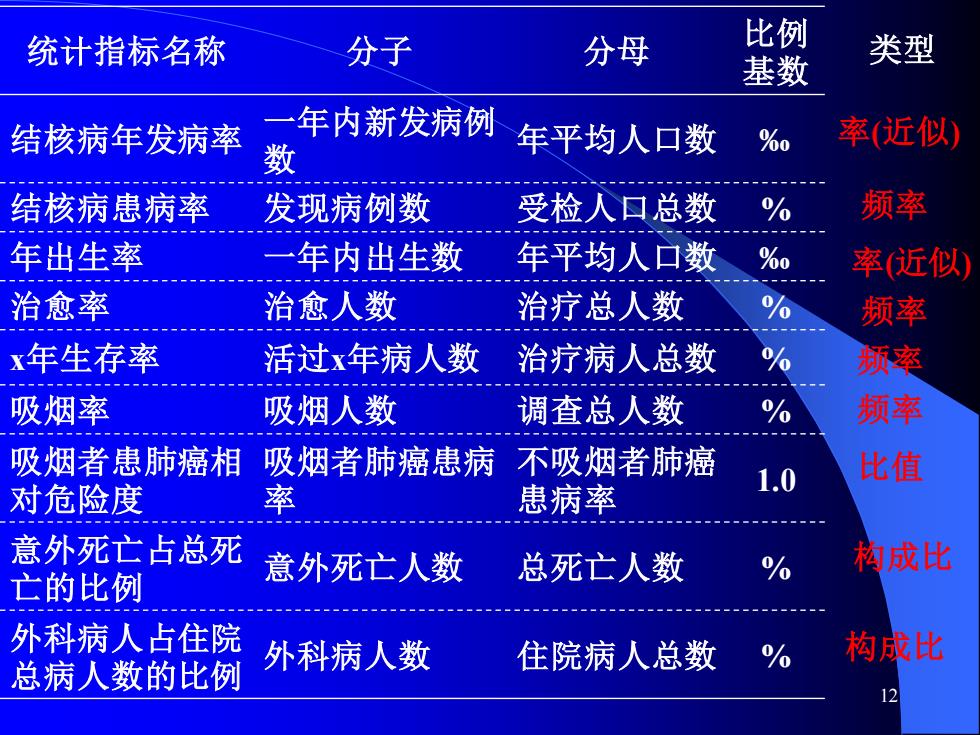
12 统计指标名称 分子 分母 比例 基数 结核病年发病率 一年内新发病例 数 年平均人口数 ‰ 结核病患病率 发现病例数 受检人口总数 % 年出生率 一年内出生数 年平均人口数 ‰ 治愈率 治愈人数 治疗总人数 % x年生存率 活过x年病人数 治疗病人总数 % 吸烟率 吸烟人数 调查总人数 % 吸烟者患肺癌相 对危险度 吸烟者肺癌患病 率 不吸烟者肺癌 患病率 1.0 意外死亡占总死 亡的比例 意外死亡人数 总死亡人数 % 外科病人占住院 总病人数的比例 外科病人数 住院病人总数 % 类型 率(近似) 频率 率(近似) 频率 频率 频率 比值 构成比 构成比
12 统计指标名称 分子 分母 比例 基数 结核病年发病率 一年内新发病例 数 年平均人口数 ‰ 结核病患病率 发现病例数 受检人口总数 % 年出生率 一年内出生数 年平均人口数 ‰ 治愈率 治愈人数 治疗总人数 % x年生存率 活过x年病人数 治疗病人总数 % 吸烟率 吸烟人数 调查总人数 % 吸烟者患肺癌相 对危险度 吸烟者肺癌患病 率 不吸烟者肺癌 患病率 1.0 意外死亡占总死 亡的比例 意外死亡人数 总死亡人数 % 外科病人占住院 总病人数的比例 外科病人数 住院病人总数 % 类型 率(近似) 频率 率(近似) 频率 频率 频率 比值 构成比 构成比

13 二、 应用相对数时的注意事项 (一) 计算相对数时,观察单位数应足够多 (二) 分析时构成比和率不能混淆 (三) 几个率的平均率不一定等于其算术平均值 (四) 相对数的相互比较应注意可比性 (五) 两个总率(平均率)比较时要注意内部构成 (六) 样本率或构成比的比较应作假设检验
13 二、 应用相对数时的注意事项 (一) 计算相对数时,观察单位数应足够多 (二) 分析时构成比和率不能混淆 (三) 几个率的平均率不一定等于其算术平均值 (四) 相对数的相互比较应注意可比性 (五) 两个总率(平均率)比较时要注意内部构成 (六) 样本率或构成比的比较应作假设检验

14 (一) 计算相对数时,观察单位数应足够多 ◆ 例如,某医师探讨某种中药配方对肺癌的治疗 效果,共治疗2例肺癌,且全部治愈,计算的治愈率 为100%。但以后其他医师用此配方治疗许多肺癌病 人,无一例治愈。由此可见,观察单位数太少时计算 结果不稳定,即样本太小缺乏代表性。不能反映事物 的客观规律,甚至有时造成错觉。 ◆ 观察单位数少时最好用绝对数表示,如果必须 用率表示,要同时列出率的可信区间。 ◆ 在动物实验中可以计算率。这是因为实验设计 周密、实验对象精选、实验条件控制严格。例如毒理 学实验,每组仅10只动物,却可计算反应率
14 (一) 计算相对数时,观察单位数应足够多 ◆ 例如,某医师探讨某种中药配方对肺癌的治疗 效果,共治疗2例肺癌,且全部治愈,计算的治愈率 为100%。但以后其他医师用此配方治疗许多肺癌病 人,无一例治愈。由此可见,观察单位数太少时计算 结果不稳定,即样本太小缺乏代表性。不能反映事物 的客观规律,甚至有时造成错觉。 ◆ 观察单位数少时最好用绝对数表示,如果必须 用率表示,要同时列出率的可信区间。 ◆ 在动物实验中可以计算率。这是因为实验设计 周密、实验对象精选、实验条件控制严格。例如毒理 学实验,每组仅10只动物,却可计算反应率

15 (二) 分析时构成比和率不能混淆 分析时常见的错误:以构成比代替率来说明问题。 ◆构成比说明事物内部各部分所占的比重或分布,不 能说明某现象发生的强度或频率大小。 例如,某地某年40岁以下、40~59岁和60岁以上三 个年龄组的人口中肿瘤死亡人数占全死亡原因的构成比 分别为21.9%、24.4%和9.4%。 上述数据为构成比,它并不说明40~59岁组肿瘤发 生情况最严重。只说明40~59岁组中因患肿瘤而死亡人 数在全部死亡人数中所占的比例比其它两个组要大。 ◆频率指标才能说明某事物发生频率的高低。 三个年龄组的肿瘤发生率分别为12.35/十万、149.14/ 十万和341.5/十万,60岁以上的肿瘤发生率最高
15 (二) 分析时构成比和率不能混淆 分析时常见的错误:以构成比代替率来说明问题。 ◆构成比说明事物内部各部分所占的比重或分布,不 能说明某现象发生的强度或频率大小。 例如,某地某年40岁以下、40~59岁和60岁以上三 个年龄组的人口中肿瘤死亡人数占全死亡原因的构成比 分别为21.9%、24.4%和9.4%。 上述数据为构成比,它并不说明40~59岁组肿瘤发 生情况最严重。只说明40~59岁组中因患肿瘤而死亡人 数在全部死亡人数中所占的比例比其它两个组要大。 ◆频率指标才能说明某事物发生频率的高低。 三个年龄组的肿瘤发生率分别为12.35/十万、149.14/ 十万和341.5/十万,60岁以上的肿瘤发生率最高
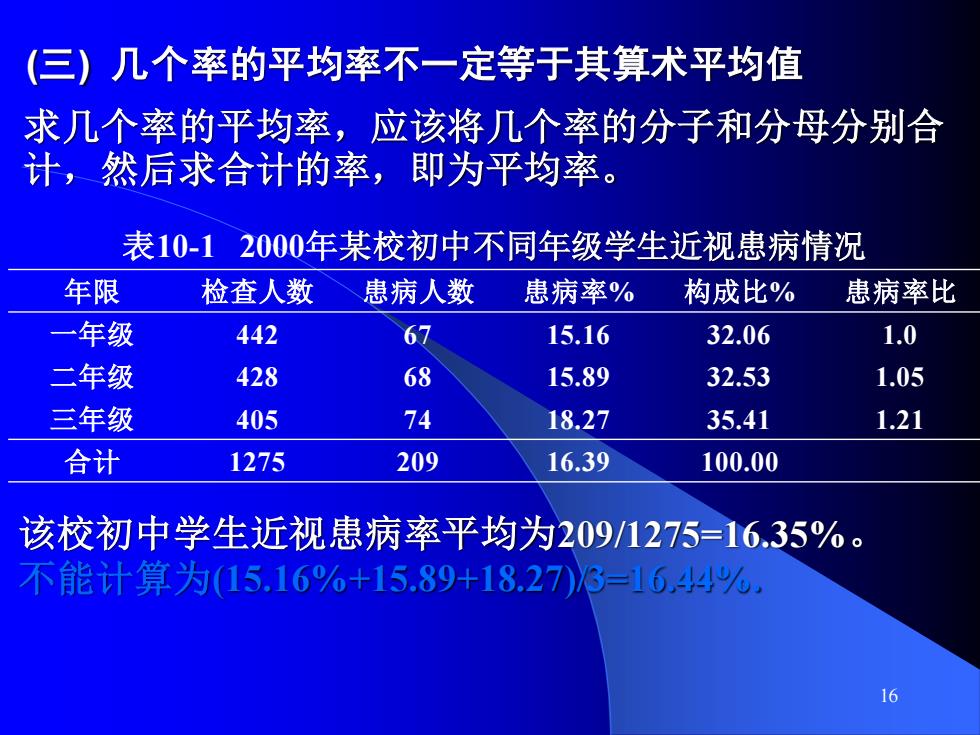
16 求几个率的平均率,应该将几个率的分子和分母分别合 计,然后求合计的率,即为平均率。 (三) 几个率的平均率不一定等于其算术平均值 表10-1 2000年某校初中不同年级学生近视患病情况 年限 检查人数 患病人数 患病率% 构成比% 患病率比 一年级 442 67 15.16 32.06 1.0 二年级 428 68 15.89 32.53 1.05 三年级 405 74 18.27 35.41 1.21 合计 1275 209 16.39 100.00 该校初中学生近视患病率平均为209/1275=16.35%。 不能计算为(15.16%+15.89+18.27)/3=16.44%
16 求几个率的平均率,应该将几个率的分子和分母分别合 计,然后求合计的率,即为平均率。 (三) 几个率的平均率不一定等于其算术平均值 表10-1 2000年某校初中不同年级学生近视患病情况 年限 检查人数 患病人数 患病率% 构成比% 患病率比 一年级 442 67 15.16 32.06 1.0 二年级 428 68 15.89 32.53 1.05 三年级 405 74 18.27 35.41 1.21 合计 1275 209 16.39 100.00 该校初中学生近视患病率平均为209/1275=16.35%。 不能计算为(15.16%+15.89+18.27)/3=16.44%