
相关知识点与学习目标 本课涉及“逻辑代数的公理、公式,逻辑函 数的最小项表达式”知识点,通过本课学习, 应掌握逻辑运算规则、逻辑函数的表示、逻辑 函数的标准表达式等基础理论
相关知识点与学习目标 本课涉及“逻辑代数的公理、公式,逻辑函 数的最小项表达式” 知识点,通过本课学习, 应掌握逻辑运算规则、逻辑函数的表示、逻辑 函数的标准表达式等基础理论
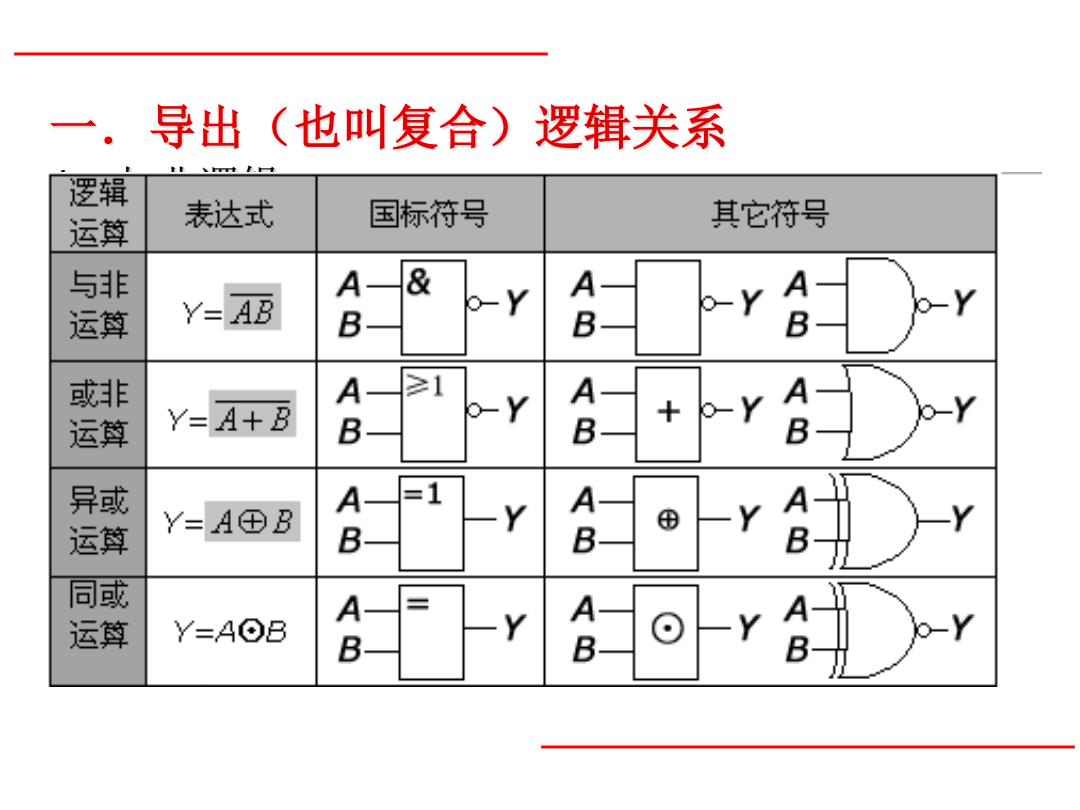
导出(也叫复合)逻辑关系 rrrt I.rt 逻辑 运算 表达式 国标符号 其它符号 与非 A-& o-Y 运算 Y=AB B -Y <m o-Y B 或非 A ≥1 o-Y A Y=A+B b-r B o-Y 运算 B 异或 A =1 A 运算 Y=A⊕B ⊕ B B B Y 同或 A- A A 运算 Y=A⊙B B B ⊙ B
一.导出(也叫复合)逻辑关系 1.与非逻辑 定义:与运算与非运算的组合称为与非逻辑 2.或非逻辑 定义:或运算与非运算的组合称为或非逻辑: 3.异或逻辑 定义:A、B不同时,输出为1, A、B相同时,输出为 0,这样的逻辑关系称为异或逻辑 4.同或逻辑 定义: A、B不同时,输出为0, A、B相同时,输出 为1,这样的逻辑关系称为同或逻辑

二.逻辑代数基本公式与常用公式 (1)逻辑代数公理 不需要加以证明,大家都公认的规律称为公理。 布尔代数中的公理有 (1)1+1=1+0=0+1=1〔1或任何数为1) (2)0+0=011=10=11=0 (3)00=01=10=0(0与任何数为0) (4)若A≠1,则A=0 若40,则A=1
二.逻辑代数基本公式与常用公式 (1)逻辑代数公理 不需要加以证明,大家都公认的规律称为公理。 布尔代数中的公理有
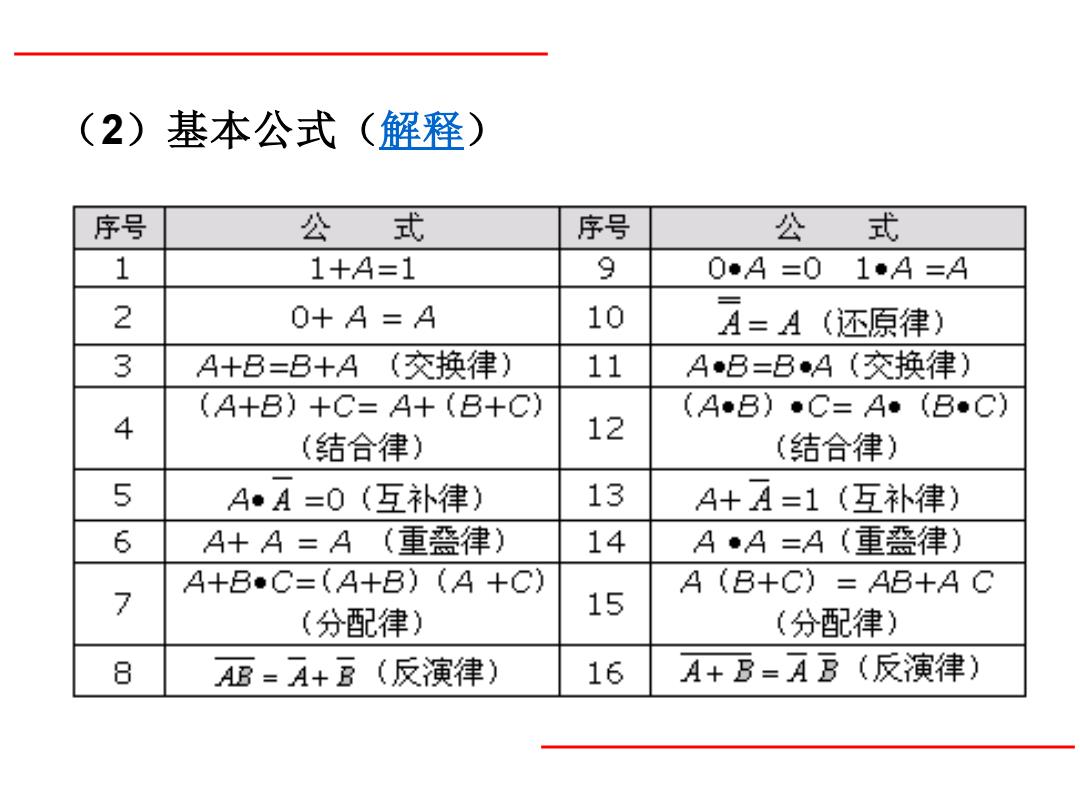
(2)基本公式(解释) 序号 公式 序号 公式 1 1+A=1 9 0●A=01●A=A 2 0+A=A 10 A=A(还原律) 3 A+B=B+A(交换律) 11 A●B=BA(交换律) (A+B)+C=A+(B+C) (A●B)·C=A·(BC) 4 (结合律) 12 (结合律) 5 A·A=0(互补律) 13 A+A=1(互补律) 6 A+A=A(重律) 14 A·A=A(重律) A+B●C=(A+B)(A+C) 4(B+C)=4B+A C 7 (分配律) 15 (分配律) 8 AB=A+B(反演律) 16 A+B=AB(反演律)
(2)基本公式(解释)
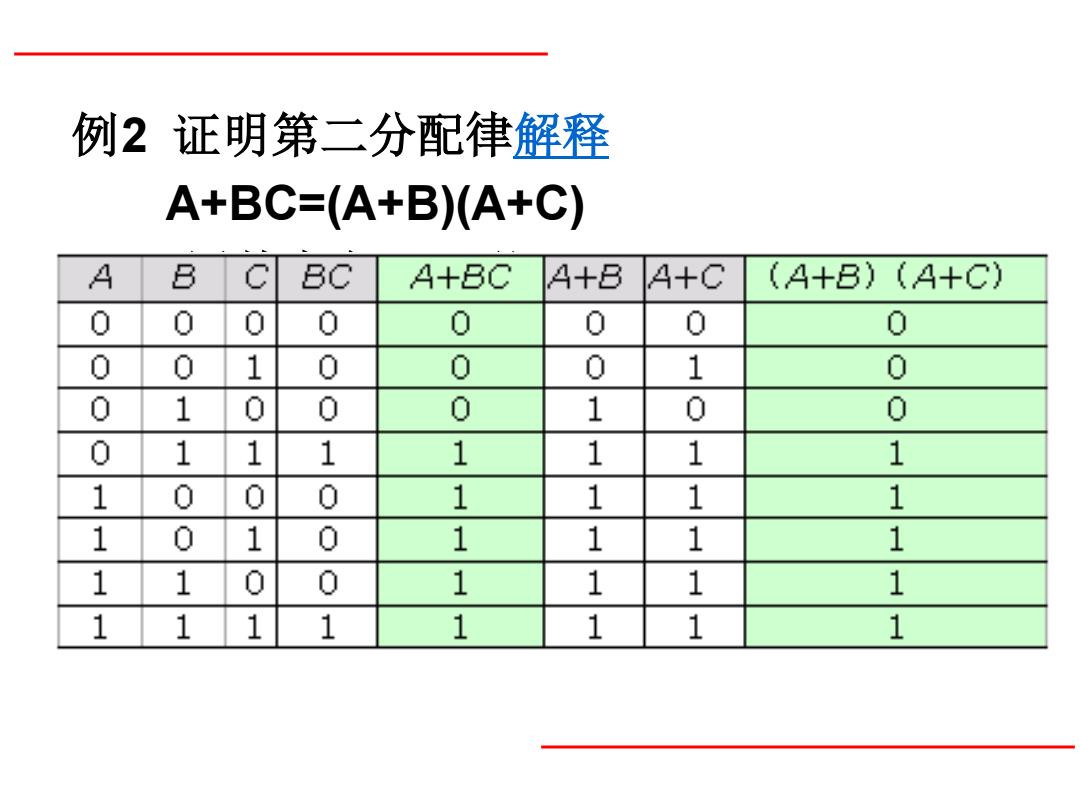
例2证明第二分配律解释 A+BC=(A+B)(A+C) A B BC A+BC 4+B 4+C (A+B)(A+C) 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 11 1 1 1 1 1
例2 证明第二分配律解释 A+BC=(A+B)(A+C) (1)用基本定理证明: (A+B)(A+C)=AA+AC+AB+BC =A+A(C+B)+BC =A[1+(C+B)]+BC =A+BC (2)用真值表证明