
直角坐标系中的分离变量法 ●Note1:a、B、y称为分离常数; ●Note2:a、b、c、d是积分常数,由边界条件确定; ●Note3:分离常数可实可虚,对应于微分方程解的三种形 式,其选取由边界条件形式决定: 。若位函数是常数,分离常数为零,选用对应的方程解 。若边界条件是周期的,微分方程解选用三角函数 。若边界条件是非周期的,微分方程解选用指数函数或者 双曲函数: 。此时,若边界是有限区域,选用双曲函数 。此时,若边界是无限区域,选用指数函数 2011年6月10日星期五 lexu@mail.xidian.edu.cn 2
2011年6月10日星期五 lexu@mail.xidian.edu.cn 12 直角坐标系中的分离变量法 Note1:α、β、γ称为分离常数; Note2:a、b、c、d是积分常数,由边界条件确定; Note3:分离常数可实可虚,对应于微分方程解的三种形 式,其选取由边界条件形式决定: 若位函数是常数,分离常数为零,选用对应的方程解 若边界条件是周期的,微分方程解选用三角函数 若边界条件是非周期的,微分方程解选用指数函数或者 双曲函数: 此时,若边界是有限区域,选用双曲函数 此时,若边界是无限区域,选用指数函数 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
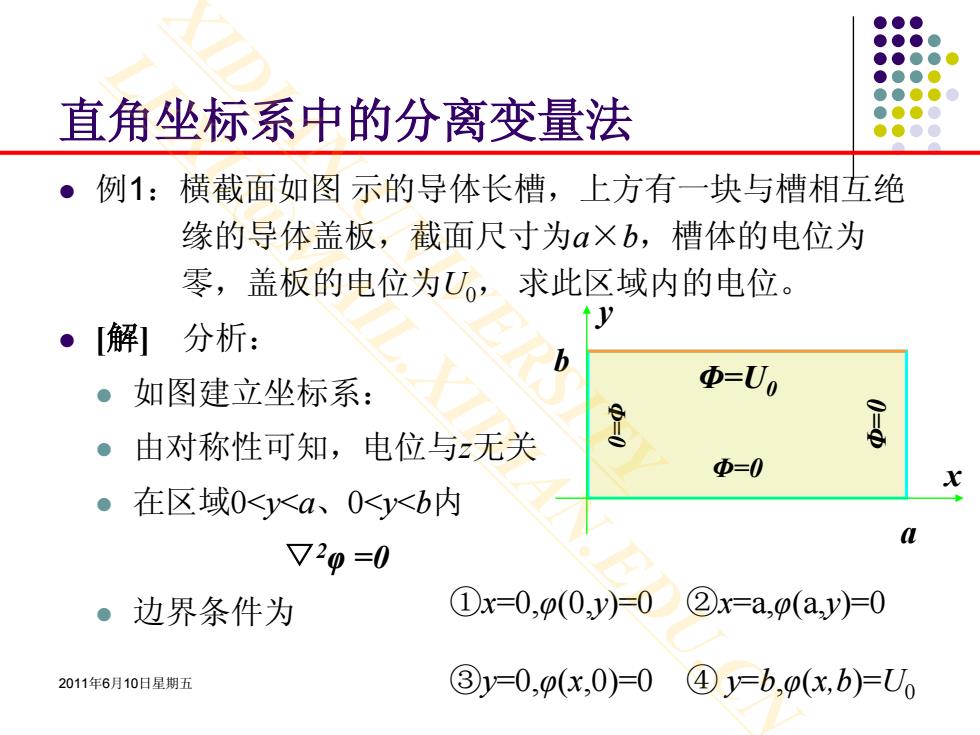
直角坐标系中的分离变量法 。例1:横截面如图示的导体长槽,上方有一块与槽相互绝 缘的导体盖板,截面尺寸为αa×b,槽体的电位为 零,盖板的电位为U,求此区域内的电位。 y ·【解]分析: 。如图建立坐标系: Φ=Uo 。由对称性可知,电位与无关 Φ=0 在区域0<y<a、0<y<b内 a 720=0 边界条件为 ①x=0,0(0,y)=0( ②x=a,p(a,y)=0 2011年6月10日星期五 ③y=0,p(x,0)=0( ④y=b,p(x,b)=U0
2011年6月10日星期五 lexu@mail.xidian.edu.cn 13 直角坐标系中的分离变量法 例1:横截面如图 示的导体长槽,上方有一块与槽相互绝 缘的导体盖板,截面尺寸为a×b,槽体的电位为 零,盖板的电位为U0, 求此区域内的电位。 [解] 分析: 如图建立坐标系: 由对称性可知,电位与z无关 在区域0<y<a、0<y<b内 ▽2φ =0 边界条件为 a b x yΦ=0 Φ=U0 Φ=0 Φ=0 ①x=0,φ(0,y)=0 ②x=a,φ(a,y)=0 ③y=0,φ(x,0)=0 ④ y=b,φ(x,b)=U0 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

直角坐标系中的分离变量法 ●假定满足电位拉普拉斯方程的解可以写成: e(x,y)=X(xY(y) ·则可以建立分离常数构成的常微方程组: X 2+B2=0 ≥B2 。考察X(x)边界条件: ●x=0,0(0,y以=0→X(0Yy以=0→X0)=0 ●x=a,p(a,以=0→X(a刨Yy=0→X(ay=0 2011年6月10日星期五 lexu@mail.xidian.edu.cn 14
2011年6月10日星期五 lexu@mail.xidian.edu.cn 14 直角坐标系中的分离变量法 假定满足电位拉普拉斯方程的解可以写成: 则可以建立分离常数构成的常微方程组: 考察X(x)边界条件: x=0, φ(0, y)=0 → X(0)Y(y)=0 → X(0)=0 x=a, φ(a, y)=0 → X(a)Y(y)=0 → X(a)=0 ϕ(, ) () () x y X xY y = 2 2 2 2 " , 0 " X a X a Y Y β β = + = = XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN