
数值积分 插值型数值积分 ●思想:用插值函数,譬如Lagrangea插值函数,代替被积函数,进行积分 f)=1.f)=L(x=2cxs=2xdx) aru 其中a,=∫心1,(x)dk ■误差估计公式 E0=Ra达-2oa ■代数精度 ●n次插值多项式形式的数值积分公式至少有n阶代数精度 11
¡ 插值型数值积分 l 思想:用插值函数,譬如Lagrange插值函数,代替被积函数,进行积分 其中 ¡ 误差估计公式 ¡ 代数精度 l 次插值多项式形式的数值积分公式至少有 阶代数精度 11 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n b b b n n i i i i a a a i i n i i i I f I f L x dx l x f x dx l x dx f x f x ( ) b i i a l x dx ( 1)( ) ( ) ( ) ( ) ( ) ( ) ( 1)! n b b x n n n n a a f E f I f I f R x dx x dx n n n

数值积分 Newton-Cotes积分:取等距节点 ■设节点步长h=60x=a+hi=0,n, 有 a=4x达-少-+M=i-少-u-md il(n-i)(-1)"- shG)”J0ru-D-i+t-1-D-0-n =(b-a).C(m) 其中Cm为仅依赖于n的常量,可事先计算 ■性质: c=1 i=0 12
¡ Newton-Cotes积分:取等距节点 ¡ 设节点步长 ,有 其中 为仅依赖于 的常量,可事先计算 ¡ 性质: 12 , , 0, , i b a h x a ih i n n 0 0 ( ) ( 1) ( 1)( 1) ( ) ( ) !( )!( 1) ( 1) ( 1) ( 1)( 1) ( ) !( )! ( ) b x a th n i i n i a n i n n i t t t i t i t n a l x dx hdt i n i nh t t t i t i t n dt i n i n b a C (n) Ci n ( ) 0 1 n n i i C
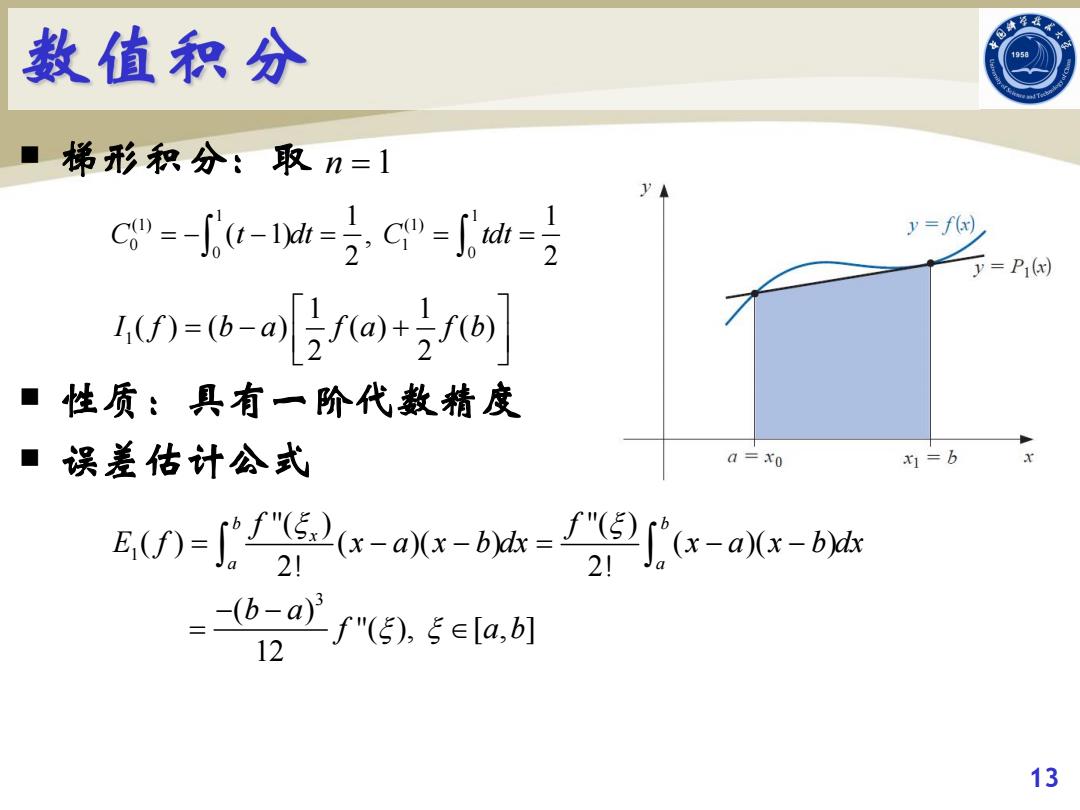
数值积分 ■梯形积分:取n=1 c"=-h=c"=h= y=f(r) y=P](x) 4=b-fa+o)】 ■性质:具有一阶代数精度 ·误差估计公式 a=x0 (-s-bK- 21 =-h-af"(5,5∈a, 12 13
¡ 梯形积分:取 ¡ 性质:具有一阶代数精度 ¡ 误差估计公式 13 n 1 1 1 (1) (1) 0 1 0 0 1 1 ( 1) , 2 2 C t dt C tdt 1 1 1 ( ) ( ) ( ) ( ) 2 2 I f b a f a f b 1 3 ''( ) ''( ) ( ) ( )( ) ( )( ) 2! 2! ( ) ''( ), [ , ] 12 b b x a a f f E f x a x b dx x a x b dx b a f a b