
Discrete differential geometry Xiao-Ming Fu
Discrete differential geometry Xiao-Ming Fu

Goal Compute approximations of the differential properties of this underlying surface directly from the mesh data. Local Averaging Region ·Normal Vectors ·Gradients Laplace-Beltrami Operator ·Discrete Curvature
Goal • Compute approximations of the differential properties of this underlying surface directly from the mesh data. • Local Averaging Region • Normal Vectors • Gradients • Laplace-Beltrami Operator • Discrete Curvature
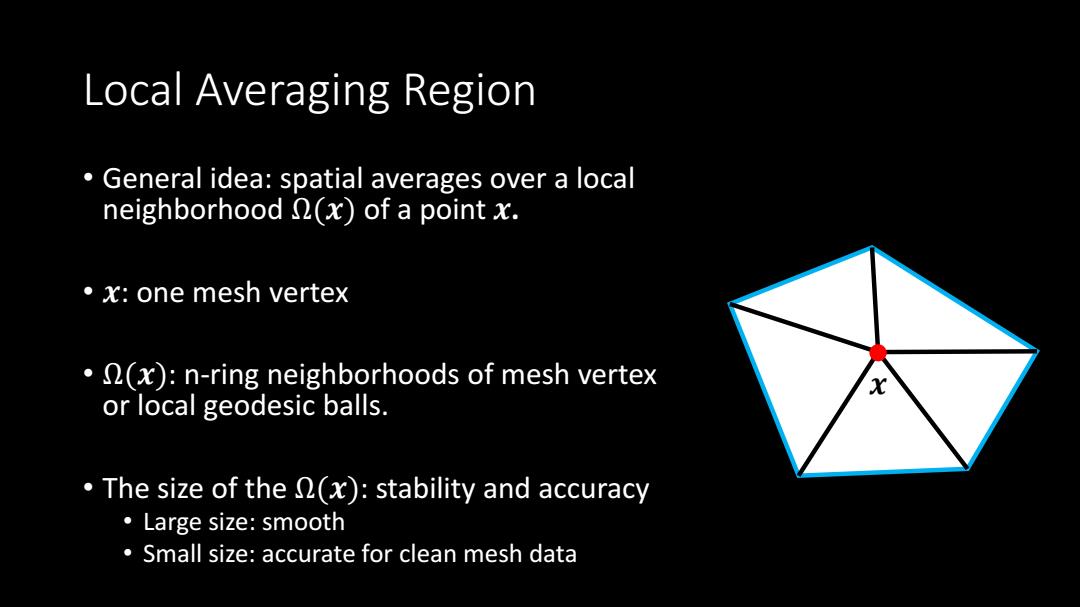
Local Averaging Region General idea:spatial averages over a local neighborhood (x)of a point x. ·x:one mesh vertex .(x):n-ring neighborhoods of mesh vertex or local geodesic balls. The size of the (x):stability and accuracy ·Large size:smooth Small size:accurate for clean mesh data
Local Averaging Region • General idea: spatial averages over a local neighborhood Ω(𝒙) of a point 𝒙. • 𝒙: one mesh vertex • Ω(𝒙): n-ring neighborhoods of mesh vertex or local geodesic balls. • The size of the Ω(𝒙): stability and accuracy • Large size: smooth • Small size: accurate for clean mesh data 𝒙
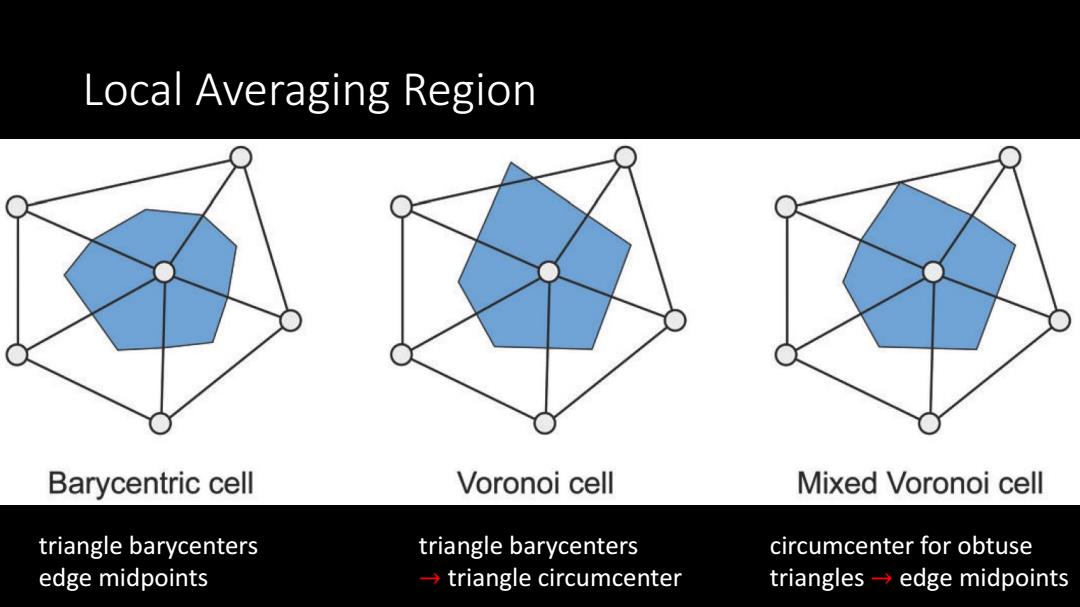
Local Averaging Region Barycentric cell Voronoi cell Mixed Voronoi cell triangle barycenters triangle barycenters circumcenter for obtuse edge midpoints triangle circumcenter triangles-edge midpoints
Local Averaging Region triangle barycenters edge midpoints triangle barycenters → triangle circumcenter circumcenter for obtuse triangles → edge midpoints

Implementation thinking How to compute the area of local average region?For example, barycentric cell. One simple idea:for each vertex,compute the area directly. ·Any improvement? How about Voronoi cell and mixed Voronoi cell?
Implementation thinking • How to compute the area of local average region? For example, barycentric cell. • One simple idea: for each vertex, compute the area directly. • Any improvement? • How about Voronoi cell and mixed Voronoi cell?