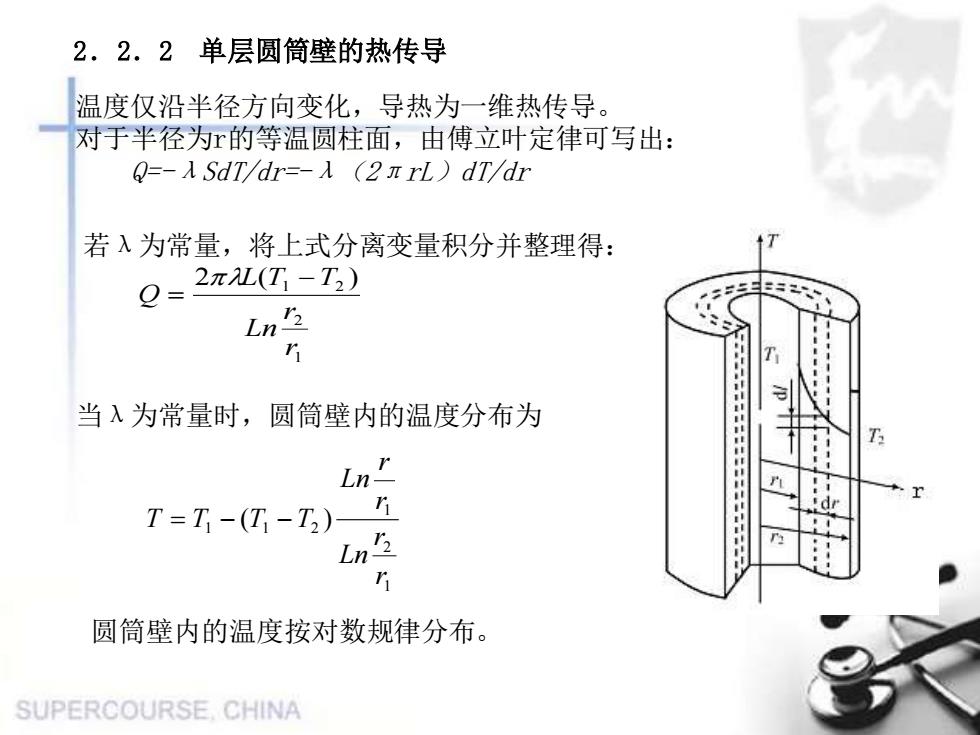
2.2.2单层圆筒壁的热传导温度仅沿半径方向变化,导热为一维热传导。对于半径为r的等温圆柱面,由傅立叶定律可写出:Q=-SdT/dr=- (2πrL) dT/dr若入为常量,将上式分离变量积分并整理得:2元(T -T)0Ln2ri当入为常量时,圆筒壁内的温度分布为TLnidrTriT =T, -(T -T2)-Ln21r圆筒壁内的温度按对数规律分布。SUPERCOURSE CHINA
1 2 1 2 2 ( ) r r Ln L T T Q − = 1 2 1 1 1 2 ( ) r r Ln r r Ln T = T − T −T 2.2.2 单层圆筒壁的热传导 温度仅沿半径方向变化,导热为一维热传导。 对于半径为r的等温圆柱面,由傅立叶定律可写出: Q=-λSdT/dr=-λ(2πrL)dT/dr 当λ为常量时,圆筒壁内的温度分布为 圆筒壁内的温度按对数规律分布。 若λ为常量,将上式分离变量积分并整理得:
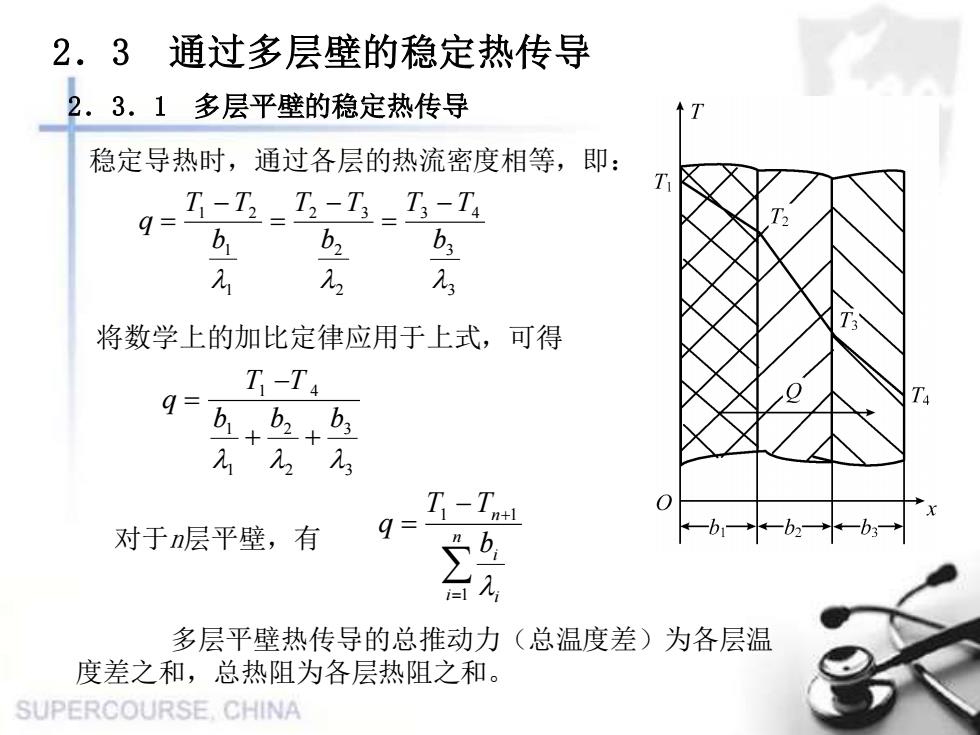
2.3通过多层壁的稳定热传导2.3.1多层平壁的稳定热传导T稳定导热时,通过各层的热流密度相等,即:TT-TT-TT-Tab,b,b2元2213将数学上的加比定律应用于上式,可得T -T4q=bi b2 b,T, Tn+1gs对于n层平壁,有多层平壁热传导的总推动力(总温度差)为各层温度差之和,总热阻为各层热阻之和。SUPERCOURSECHINA
3 3 3 4 2 2 2 3 1 1 1 2 b T T b T T b T T q − = − = − = 3 3 2 2 1 1 1 4 b b b T T q + + − = = − + = n i i i n b T T q 1 1 1 2.3 通过多层壁的稳定热传导 稳定导热时,通过各层的热流密度相等,即: 将数学上的加比定律应用于上式,可得 对于n层平壁,有 多层平壁热传导的总推动力(总温度差)为各层温 度差之和,总热阻为各层热阻之和。 2.3.1 多层平壁的稳定热传导
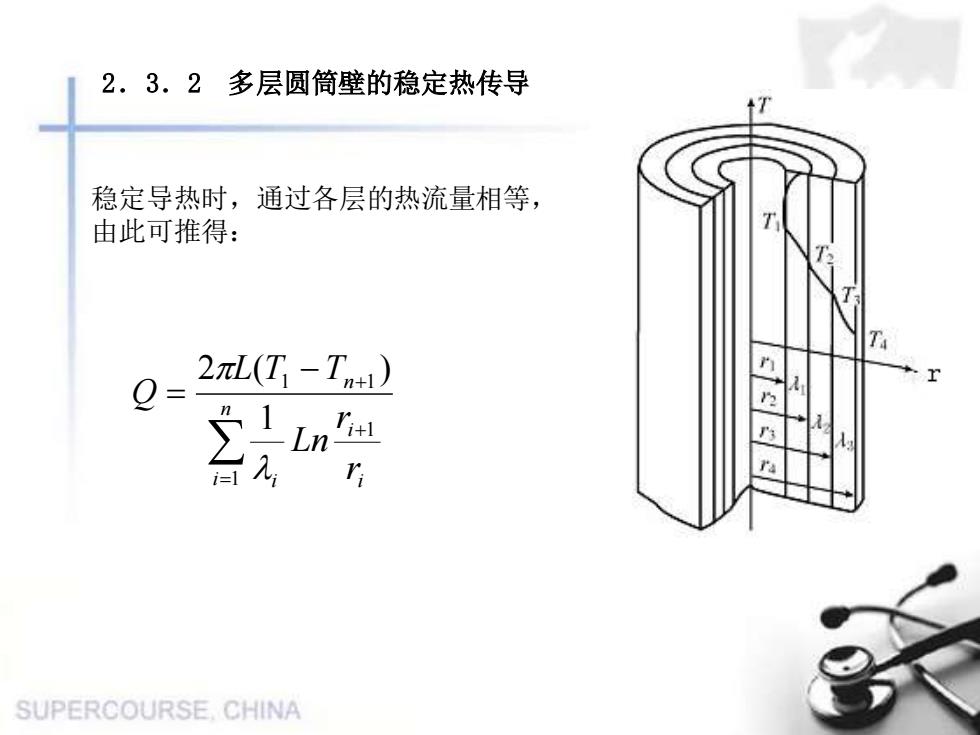
2.3.2多层圆筒壁的稳定热传导稳定导热时,通过各层的热流量相等,由此可推得:2元L(T -Tn+1)0ZILnri+1后元rSUPERCOURSE CHINA
= + − + = n i i i i n r r Ln L T T Q 1 1 1 1 1 2 ( ) 2.3.2 多层圆筒壁的稳定热传导 稳定导热时,通过各层的热流量相等, 由此可推得:

[例2-1]某冷库壁面由0.076m厚的混凝土外层,0.100m厚的软木中间层及0.013m厚的松木内层所组成。其相应的热导率为:混凝土0.762W/(m·K):软木0.0433W/(m·K):松木0.151W/(m·K)。冷库内壁面温度为-18℃,外壁面温度为24℃。求进入冷库的热流密度以及松木与软木交界面的温度。解:三层的导热,T1=24℃,T4=-18℃;b1=0.076 m, b2=0.100 m, b3=0. 013 m;Λ1=0.762W/ (m·K),Λ2-0.0433 W/ (mK),Λ3=0. 151 W/ (m· K)。(1)计算热流密度qT, -T 424 -(-18)= 16.8W / mqbi+ b+ b30.0760.1000.0130.1510.7620.0433(2)计算松木与软木交界面的温度T3由q=(T3-T) /b3得T,=T4+qb,/ α 3=-18+16. 8 X0. 013/0. 151=-16. 6 ℃SUPERCOURSECHINA
[例2-1] 某冷库壁面由0.076 m厚的混凝土外层,0.100 m厚的软木中 间层及0.013 m厚的松木内层所组成。其相应的热导率为:混凝土0.762 W/(m·K);软木0.0433 W/(m·K);松木0.151 W/(m·K)。冷库内壁面温 度为-18 ℃,外壁面温度为24 ℃。求进入冷库的热流密度以及松木与软 木交界面的温度。 2 3 3 2 2 1 1 1 4 16.8 / 0.151 0.013 0.0433 0.100 0.762 0.076 24 ( 18) W m b b b T T q = + + − − = + + − = (2)计算松木与软木交界面的温度T3 由 q=λ3 (T3 -T4 )/b3 得 T3 =T4 +qb3 /λ3 =-18+16.8×0.013/0.151=-16.6 ℃ 三层的导热,T1=24 ℃,T4=-18 ℃; b1=0.076 m,b2=0.100 m,b3=0.013 m; λ1=0.762 W/(m·K),λ2=0.0433 W/(m·K), λ3=0.151 W/(m·K)。 解: (1)计算热流密度q

[例2-2】内径为25.4mm,外径为50.8mm的不锈钢管,其热导率为21.63W/(m·K)。外包厚度为25.4mm的石棉保温层,其热导率为0.2423W/(m·K)。管的内壁面温度为538℃,保温层的外表面温度为37.8℃,计算钢管单位长度的热损失及管壁与保温层分界面的温度。解:两层的导热,T1=538℃,T3-37.8℃;r1=0.0254/2=0.0127m,r2=00508/2=0.0254m,r3-r2+b=0.0254+0.0254=0.0508m;Λ1=21.63 W/(m:K)N2=0.2423 W/ (m·K)。(1)单位管长的热损失Q/LQ2元(T-T)1LI2+LnLn元22r22元(538-37.8)1086W/m0.0254110.0508LnTn21.630.24230.02540.0127SUPERCOURSE CHINA
W m Ln Ln r r Ln r r Ln T T L Q 1086 / 0.0254 0.0508 0.2423 1 0.0127 0.0254 21.63 1 2 (538 37.8) 1 1 2 ( ) 2 3 1 2 2 1 1 3 = + − = + − = [例2-2] 内径为25.4 mm,外径为50.8 mm的不锈钢管,其热导率为21.63 W/(m·K)。外包厚度为25.4 mm的石棉保温层,其热导率为0.242 3 W/(m·K)。管的内壁面温度为538 ℃,保温层的外表面温度为37.8 ℃,计 算钢管单位长度的热损失及管壁与保温层分界面的温度。 (1)单位管长的热损失Q/L 两层的导热,T1=538 ℃,T3=37.8℃; r1=0.0254/2=0.0127m, r2=0050 8/2=0.025 4m, r3=r2+b=0.0254+0.0254=0.0508m; λ1=21.63 W/( m·K) λ2=0.2423 W/( m·K)。 解: