
Chap:A The representslion for the states and dynamical varls 例3:求坐标表象中F的矩阵元 F=∫6ex-x)fx",-ii最)x-x)”=F(x,-ii)6(x'-x) 例4:求动量表象中F的矩阵元 要计算此积分,需要 知道F的具体形式. Fp=了yn*(x)F(x,一ih录)wp(x) (1) =p (2) f=x xm=∫y,*(x)xwn(x)dk Pm=∫9n*()ny(x) 2∫1etow,tee -pv,*(v,(xdx =p'6(p-p') cy,h =(i)yp*(xΨ(x =(h品)6(p-p') 21
Chap.4 The representation for the states and dynamical variable 21 例3:求坐标表象中F的矩阵元 xx −= ′′′′ − x ′ − xdxxixFxxF ′′′′ ∂ ′′ ∂ ′ ∫ )(),( ˆ δ )( = δ 例 4: 求动量表象中 F的矩阵元 F dxxixFx pp p x p′ )(),()(* ∂ ∂ ′ = − ∫ ψ = ψ 要计算此积分,需要 知道 F 的具体形式. pF ˆ ˆ ).1( = ppi )()( p = − ′ ∂ ∂ = δ )(),( ˆ −= ∂x ′ − xxixF ∂ = δ p pp ′ p )(* ˆ p′ )( dxxpx ∫ = ψψ p p′ )()(* dxxxp ∫ = ′ ψψ = ′δ − ppp ′)( i dxxx p p p )()(*)( ∂ ′ ∂ ∫ = = ψψ dxxei p ipx p )()( 2 1 / ′ − ∂ ∂ ∫ = ψ π = = = dxxxe p ipx )(][ 2 1 / ′ − ∫ = ψ π = = x dxxxx pp p p ′ ′ )()(* ∫ = ψψ ).2( ˆ = xF

Chap.4 The representation for the states and dynamical varlable §3量子力学公式的矩阵表述 (一) 平均值公式 (二)本征方程 (三)Schrodinger方程的矩阵形式 22
Chap.4 The representation for the states and dynamical variable 22 (一)平均值公式 (二)本征方程 (三)Schrodinger方程的矩阵形式 §3 量子力学公式的矩阵表述
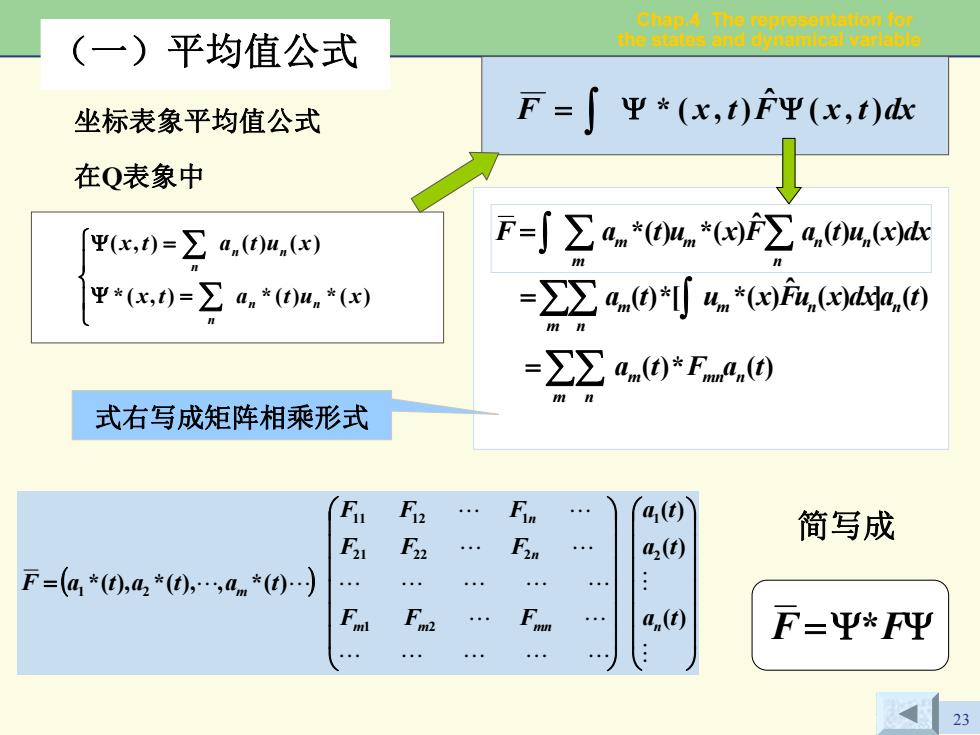
Chap.A The representslion for (一)平均值公式 the stetes and dynamical varlable 坐标表象平均值公式 F=∫ 平*(x,t)FY(x,t)dc 在Q表象中 平x,)=∑a,(0u.x) F=∫∑an*0u*6wF∑a,0m,ws Ψ*(x,)=∑ Ca *(t)u *(x) =∑∑a④*可4n*(i.wd, =∑∑an0*Fnn0 式右写成矩阵相乘形式 F2 a,() 简写成 E F2 a2(t) F=a,*(),2*(0),0m*(0) : F a,(t) F=平*FΨ 。 23
Chap.4 The representation for the states and dynamical variable 23 坐标表象平均值公式 F ),( dxtxFtx ˆ ∫ Ψ= ),(* Ψ 在Q表象中 ⎪⎩ ⎪⎨⎧ =Ψ =Ψ ∑∑ )(*)(*),(* )()(),( xutatx xutatx n n n nn n xutaFxutaF dx nn n m m m )()( ˆ = ∫ ∑ )(*)(* ∑ 式右写成矩阵相乘形式 简写成 F =Ψ*FΨ )(])( ˆ )(*[*)( tadxxuFxutam m n n m n ∑∑ ∫ = taFta )(*)( m nmn m n =∑∑ (一)平均值公式 ( ) ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ = ## """"" " """""" " " " " "" )( )( )( )(*,),(*),(* 21 1 2 21 22 2 11 12 1 1 2 ta ta ta FF F FF F FF F tatataF m m mn n nn m
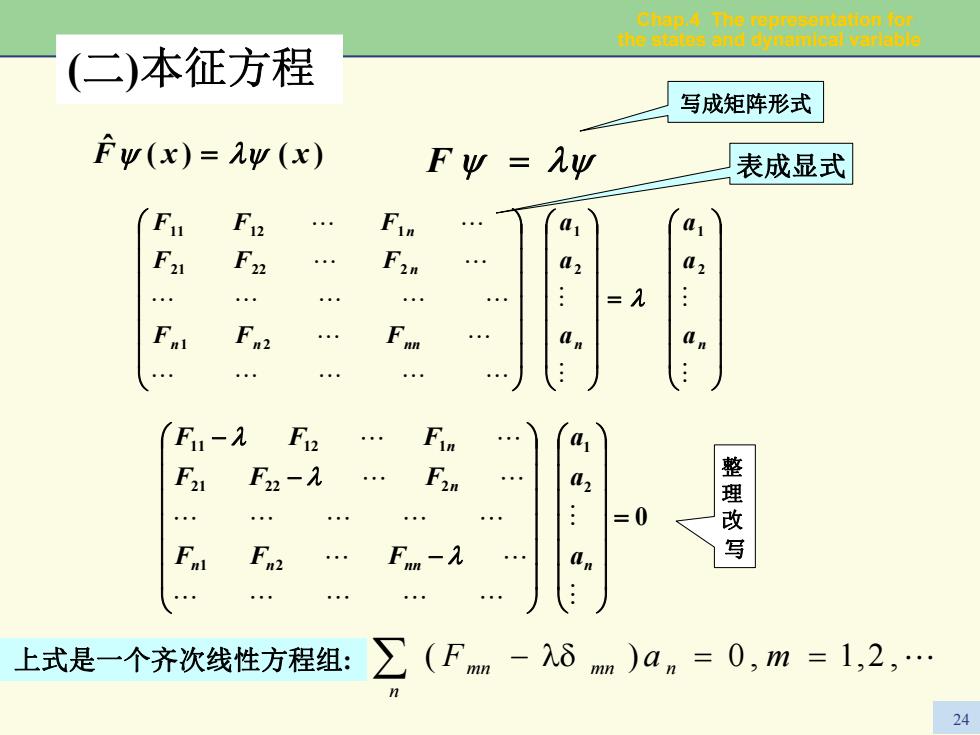
Chap.4 The representstion for the states and dynamical varlable (二)本征方程 写成矩阵形式 Fw(x)=Av (x) Fy=九 表成显式 Fu Fin F21 Fn F2n 02 02 . .: =2 F F1-2 F2 1 F2-九 2 =0 整理改 Fnm-入 00 上式是一个齐次线性方程组: ∑(Fmm-入δm)an=0,m=1,2,. 24
Chap.4 The representation for the states and dynamical variable 24 )()( ˆ = λψψ xxF 写成矩阵形式 F ψ = λψ 表成显式 ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ = ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ ## ## """"" " """""" " " " " n n nn n n nn aaa aaa FF F FF F FF F 21 21 1 2 21 22 2 11 12 1 λ 整 理 改 写 0 2 1 1 2 21 22 2 11 12 1 = ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ − − − ## """"" " """""" " " " " n n nn n nn aaa FF F FF F F F F λ λ λ 上式是一个齐次线性方程组: ∑ ( F λδ− ma == ,2,1,0) " n mn nmn (二)本征方程
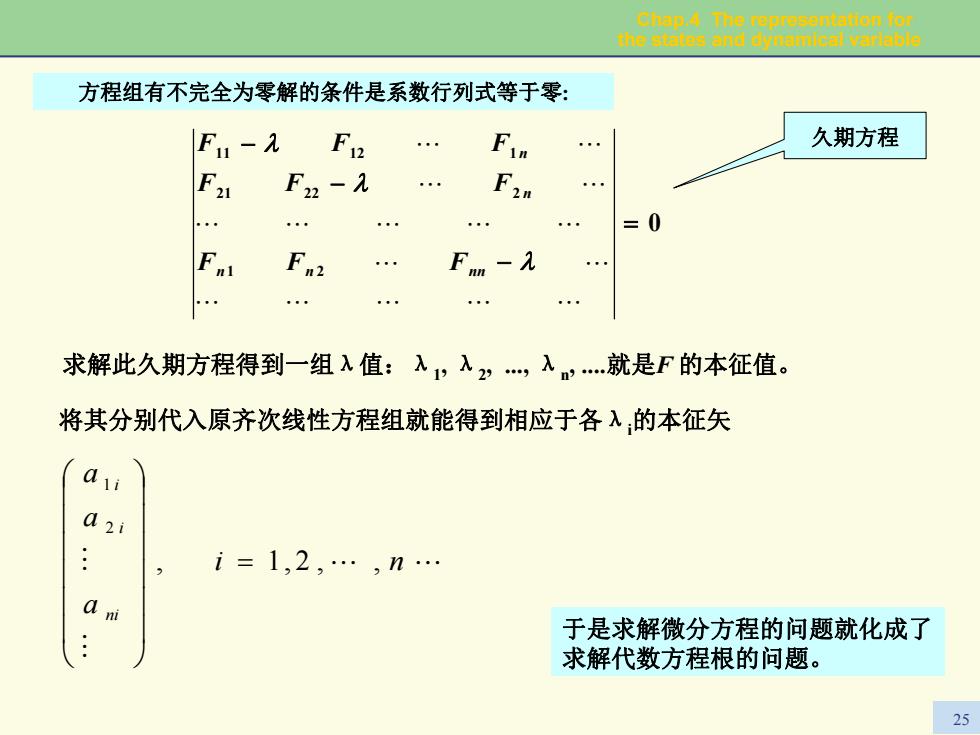
Chap.A The representstlon for the states and dynamical varlable 方程组有不完全为零解的条件是系数行列式等于零: F1- 久期方程 F22-2 三0 求解此久期方程得到一组入值:入1,入2”,入.就是F的本征值。 将其分别代入原齐次线性方程组就能得到相应于各λ,的本征矢 a2i : i=1,2,.,n. a ni 于是求解微分方程的问题就化成了 求解代数方程根的问题。 25
Chap.4 The representation for the states and dynamical variable 25 方程组有不完全为零解的条件是系数行列式等于零: 0 1 2 21 22 2 11 12 1 = − − − """"" " " """"" " " " " λ λ λ n n nn n n FF F FF F F F F 久期方程 求解此久期方程得到一组λ值:λ1, λ2, ., λn, .就是F 的本征值。 将其分别代入原齐次线性方程组就能得到相应于各λi的本征矢 "" # # i n a a a ni i i ,2,1, 2 1 = ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ 于是求解微分方程的问题就化成了 求解代数方程根的问题