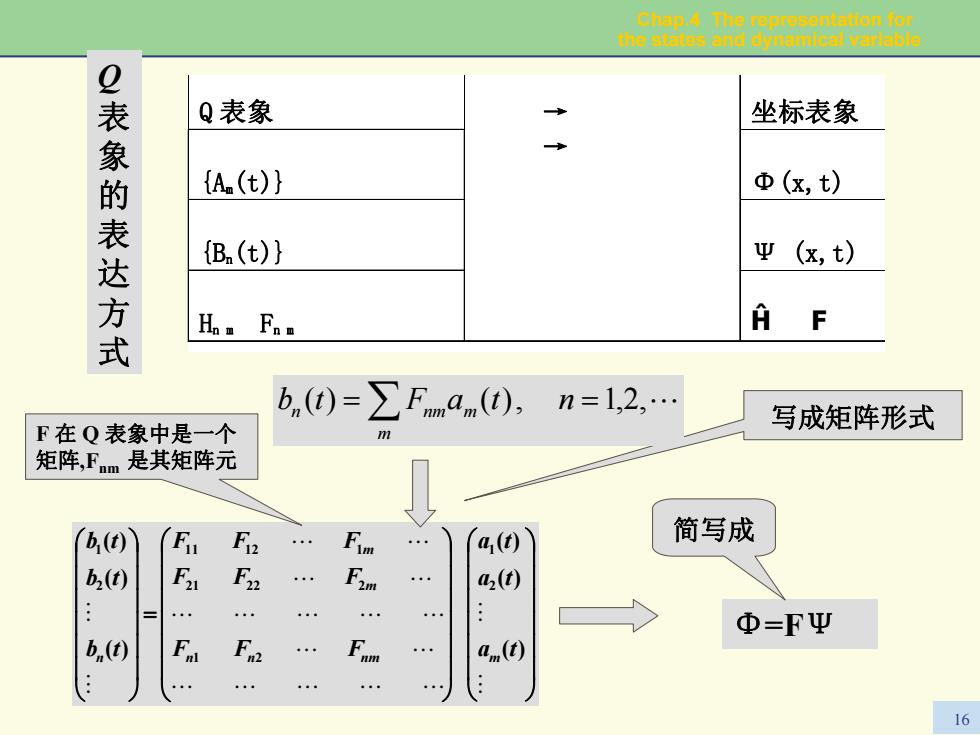
Chap.4 The representation for the states and dynamical varlable Q表象 Q表象 坐标表象 {A(t) 中(x,t) 表达方式 {B(t)} Ψ(x,t) H。Fmn A bn(0)=∑Fm(),n=l,2,. F在Q表象中是一个 写成矩阵形式 m 矩阵,Fm是其矩阵元 b(t) f Fw a(t) 简写成 b2(t) Fn a(t Φ=FΨ b,(t) Fa a(t) 。 。 16
Chap.4 The representation for the states and dynamical variable 16 Q 表 象 的 表 达 方 式 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ # # """"" " " """"" " " " " # # )( )( )( )( )( )( 2 1 1 2 21 22 2 11 12 1 2 1 ta ta ta FF F FF F FF F tb tb tb n n nm m m m n F 在 Q 表象中是一个 矩阵,Fnm 是其矩阵元 Φ=F Ψ 简写成 Q 表象 坐标表象 {A m(t)} Φ(x,t) {Bn(t)} Ψ (x,t) Hn m Fn m → → Ĥ F 写成矩阵形式 )( = ∑ ntaFtb = ,2,1,)( " m n mnm

Chap.4 The representallon for the states and dynamical varlable 例1:求L,在L2,L,共同表象,=1子空间中的矩阵表示。 令:u1=Y1u2=Y10,u3=Y1-1 则L的矩阵元可如下计算: (Lg=∫4,*i4, L矩阵是3×3矩阵 i,j=1,2,3 计算中 L=心+i) 使用了 =+i川方 LYm =hI(1+1)-m(m1)Yi.m+ 公式 +i方+X 写 010 同理可得L,Lz d+ig方。 L:= 101 0-i0 阵 010 L,= i 0-i L在自身表象中具有最简 0 i 由此得L,矩阵元: 单形式,是一个对角矩阵, 对角元素就是L的本征值。 1 0 0 (L)11=(L22=(L)39=0 L:= 0 0 0 L18=(L31=0 .0 0 (L12=(L21=()23=(L)32=/、2 17
Chap.4 The representation for the states and dynamical variable 17 写 成 矩 阵 例 1:求 Lx 在 L 2, L z共同表象, A=1子空间中的矩阵表示。 令: u1 = Y11 u 2 = Y10 , u 3 = Y1-1 3,2,1, ˆ *)( = = ∫ Ω ji ijx jxi duLuL L x矩阵是 3 × 3矩阵 ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ =+= =+= + =+= −−+ −+ − −+ 3 11 10 2 10 1111 1 11 10 2 1 ) ˆˆ ( 2 1 )( 2 1 ) ˆˆ ( 2 1 2 1 ) ˆˆ ( 2 1 YLLuL Y YLLuL YY YYLLuL x x x = = = 1, 2 1 )1()1( ) ˆˆ ( ± ± −+ ±−+= += lm ml x YmmllYL LLL = 计算中 使用了 公式 由此得 L x矩阵元: ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 100 000 001 Lz = Lz在自身表象中具有最简 单形式,是一个对角矩阵, 对角元素就是 Lz的本征值。 同理可得 Ly L z 则 Lx 的矩阵元可如下计算: ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − = 00 0 00 2 i ii i Ly = (L x )11 = (L x )22 =(L x )33 =0 (L x )13 = (L x )31 =0 (L x )12 = (L x )21 =(L x )23 =(L x )32 = = / 2 0 1 0 1 0 1 2 0 1 0 Lx ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ =
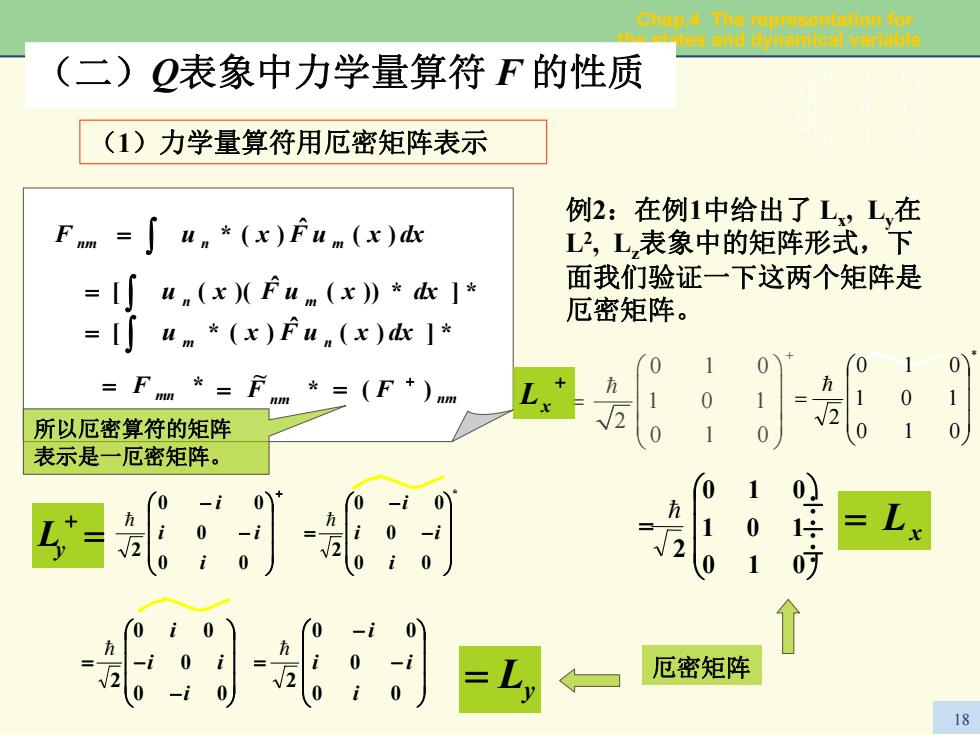
Chap4 The representstion for -es and dynamical varlable (二)Q表象中力学量算符F的性质 (1)力学量算符用厄密矩阵表示 例2:在例1中给出了L,L,在 Fm=∫un*(x)Fum(x)dk L2,L表象中的矩阵形式,下 =[un(x)(Fum(x》*k1* 面我们验证一下这两个矩阵是 =[了um*(x)Fun(x)kI* 厄密矩阵。 0 1 0 0 1 0 =Fm六=nm*=(F+)m 九 nm 1 0 0 1 所以厄密算符的矩阵 √2 0 1 0 0 表示是一厄密矩阵。 0 1 0 1 0 0 0 0 2 厄密矩阵 0 o i 18
Chap.4 The representation for the states and dynamical variable 18 ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ − −= 00 0 00 2 i ii i = (1)力学量算符用厄密矩阵表示 F nm n m )( dxxuFxu ˆ )(* ∫ = *]*))( ˆ n )(([ m dxxuFxu ∫ = *])( ˆ m )(*[ n dxxuFxu ∫ = = F mn * * ~ = F nm F nm )( + = 所以厄密算符的矩阵 表示是一厄密矩阵。 例2:在例1中给出了 Lx, Ly在 L2, Lz表象中的矩阵形式,下 面我们验证一下这两个矩阵是 厄密矩阵。 = Ly 0 1 0 1 0 1 2 0 1 0 + ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = = Lx + Lx ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ − − = 0 0 0 0 0 2 i i i i = + ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ − − 0 0 0 0 0 2 i i i i = =+ Ly 厄密矩阵 * 0 0 0 0 0 2 ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ − − = i i i i = * 0 1 0 1 0 1 0 1 0 2 ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ = (二) = Q表象中力学量算符 F 的性质 * 0 1 0 1 0 1 0 1 0 2 ⎟⎟⎟⎠⎞ ⎜⎜⎜⎝⎛ = = ÷ ÷ ÷ ⎠ ⎞ ⎜⎜⎜⎝⎛ = 0 1 0 1 0 1 0 1 0 2=

Chap.4 The representallon for the states and dynamical varlable (2)力学量算符在自身表象中的形式 Qu(x)=C.u(x) 结论: 算符在自身表象中是一 Q的矩阵形式 对角矩阵,对角元素就 是算符的本征值。 2m=∫un*(x)0un(x)dk 0 =m∫un*(x)ln(x)d 0 0 =2nδnm 0= 0 19
Chap.4 The representation for the states and dynamical variable 19 (2)力学量算符在自身表象中的形式 )()( ˆ n = nn xuQxuQ Q的矩阵形式 nmm nm m nm n m Q dxxuxuQ dxxuQxuQ = δ = = ∫ ∫ )()(* )( ˆ )(* 结论: 算符在自身表象中是一 对角矩阵,对角元素就 是算符的本征值。 ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ = """"""" """"" """"""" """" """"" Qn Q Q Q 00 00 02 1
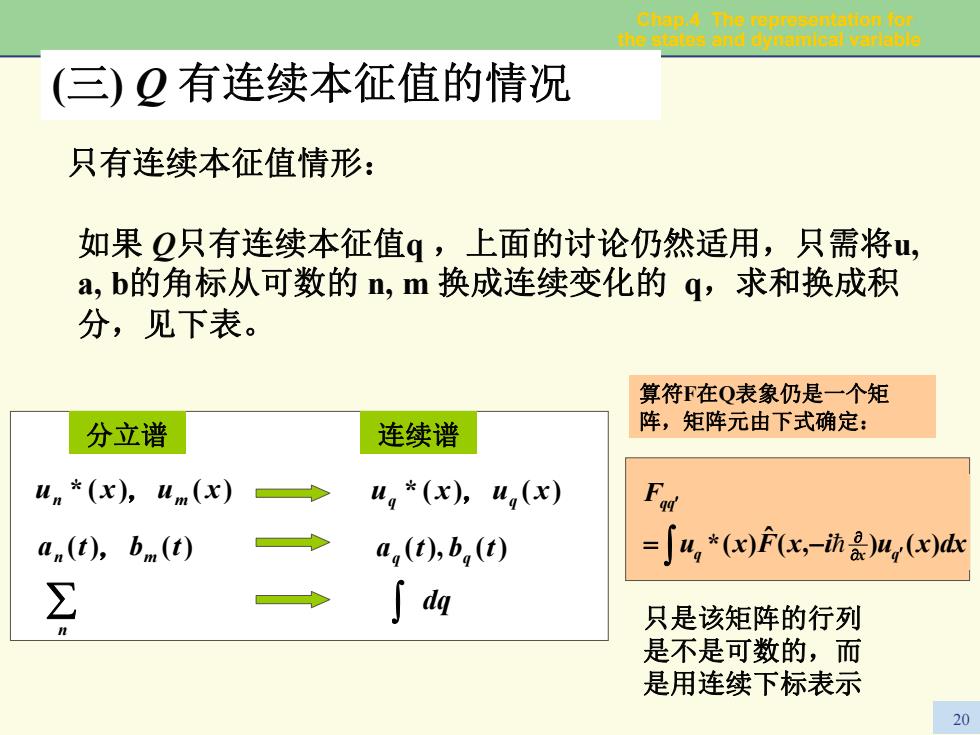
Chap.4 The representstion for the states and dynamical varlable (三)Q有连续本征值的情况 只有连续本征值情形: 如果Q只有连续本征值q,上面的讨论仍然适用,只需将u, a,b的角标从可数的n,m换成连续变化的q,求和换成积 分,见下表。 算符F在Q表象仍是一个矩 分立谱 连续谱 阵,矩阵元由下式确定: un*(x),Lm(x) u,*(x),4,(x) an(t),bm(t) a,(t),b,(t) =∫4,*(x)Fc,-ih晨)4(x) ∑ ∫dg 只是该矩阵的行列 是不是可数的,而 是用连续下标表示 20
Chap.4 The representation for the states and dynamical variable 20 只有连续本征值情形: 如果 Q只有连续本征值q ,上面的讨论仍然适用,只需将u, a, b的角标从可数的 n, m 换成连续变化的 q,求和换成积 分,见下表。 分立谱 连续谱 xuxu )()(* n , m tbta )()( n , m ∑ n dq ∫ tbta )(),( qq xuxu )()(*q , q 算符F在Q表象仍是一个矩 阵,矩阵元由下式确定: ∫ ∂ ′ ∂ ′ = − dxxuixFxu F q x q qq )(),( ˆ )(* = 只是该矩阵的行列 是不是可数的,而 是用连续下标表示 (三) Q 有连续本征值的情况