《量子力学》课程教学资源（习题解答）第三章 量子力学中的力学量

周世勋量子力学教程第三章习题解答 3.1一维谐振子处在基态x)= a V√π (1)势能的平均值可= 222 (2②)动能的平均值T= 4 (3)动量的几率分布函数。 解0=ore@2erh 2a34o2.h o =h@ x2eard在=135.(2n-) 元 4 2a”Va aF-上vaaa V2nEA-aix a方2 ialLods-a[ Vπ2 2a 盟- a2=.o 4u方 =40 (3)c(p)=∫y。(x)w(x)dk

1 周世勋 量子力学教程 第三章习题解答 3.1 一维谐振子处在基态 t x i x e      2 2 2 2 ( ) − − = ，求： (1)势能的平均值 2 2 2 1 U =  x ； (2)动能的平均值 2 2 p T = ； (3)动量的几率分布函数。 解：(1)   − − U = x = x e dx x 2 2 2 2 2 2 2 1 2 1                 =  = =  2 2 2 2 2 2 4 1 2 1 2 1 2 1 2 2 1  4 1 =   + −     − = 0 1 2 2 2 1 3 5 (2 1) a a n x e dx n n n ax   (2)   − = = x p x dx p T ( ) ˆ ( ) 2 1 2 * 2 2       − − − = − e dx dx d e x x 2 2 2 2 2 1 2 2 2 2 1 ( ) 2 1         − − = − x e dx x 2 2 (1 ) 2 2 2 2 2        [ ] 2 2 2 2 2 2 2 2 2    − −  − − = e dx − x e dx  x  x       ] 2 [ 2 3 2 2 2          = −                 = = =  2 2 4 4 2 2 2 2 2  4 1 = 或    4 1 4 1 2 1 T = E −U = − = (3)  c p = x x dx p ( ) ( ) ( ) *  

上层 层产。h a层哈步在 e 2元 点层本 =2 a 动量几率分布函数为 op)-k(p # ah 3.2.氢原子处在基态(，0，p)=- 应 (1)r的平均值： ②势能-上的平均值 (3)最可几半轻. (4)动能的平均值： (5)动量的几率分布函数。 gwr-jrwaofirrern8daoao 汇x"ed= a =433 a 2

2 2 1 2 2 2 1   − − − = e e dx Px i x         − − − = e e dx Px i x   2 2 2 1 2 1       − − + − = e dx ip p x 2 2 2 2 2 2 2 ( ) 2 1 2 1            − − − + = e e dx ip x p 2 2 2 2 2 2 ( ) 2 1 2 2 1                2 2 1 2 2 2 2   p e − = 2 2 2 2 1      p e − = 动量几率分布函数为 2 2 2 1 ( ) ( ) 2       p p c p e − = = # 3.2.氢原子处在基态 0 / 3 0 1 ( , , ) r a e a r − =     ，求： (1)r 的平均值； (2)势能 r e 2 − 的平均值； (3)最可几半径； (4)动能的平均值； (5)动量的几率分布函数。 解：(1)           re r drd d a r r r d r a sin 1 ( , , ) 0 2 2 0 0 2 / 3 0 2 0      − = =   − = 0 3 2 / 3 0 0 4 r a dr a r a   + − = 0 1 ! n n ax a n x e dx 4 0 0 3 0 2 3 2 4 3! a a a =         =

a0-e-云frn0n6o 云em9wo 营d s-4e21 (3)电子出现在r+d球壳内出现的几率为 o(rydr=L(r.0.r'sin 0drd0 do=dr )=4 do(r)=4 (2-2r)re dr ao ao 令do0=0,→5=0,5=0,5=a r 当片=0,5=o时，r)=0为几率最小位置 dio(r)=4 dr2 e0 d'o(r) .r=a。是最可几半径。 1 a T=盆0e gre心pm0a0o e-e灬女 2 do 3

3 0 2 2 0 3 0 2 0 2 / 3 0 2 0 2 0 0 2 / 3 0 2 0 2 0 0 2 / 2 3 0 2 2 2 4 1 4 sin sin 1 (2) ( ) 0 0 0 a e a a e e r dr a e e r drd d a e e r drd d a r e r e U r a r a r a = −         = − = − = − = − = −         −  −  −             (3)电子出现在 r+dr 球壳内出现的几率为   =          0 2 0 2 2 (r)dr [ (r, , )] r sin drd d e r dr a 2r / a 2 3 0 0 4 − = 2 / 2 3 0 0 4 ( ) e r a r − r a  = 0 2 / 0 3 0 ) 2 (2 ( ) 4 r a r re dr a a d r − = −  令 1 2 3 0 0 0, , ( ) r r r a dr d r = ， = =  =  当 r1 = 0, r2 = 时，(r) = 0 为几率最小位置 0 2 2 / 2 0 0 3 0 2 2 ) 8 4 (2 ( ) 4 r a r e a r dr a a d r − = − +  0 ( ) 8 2 3 0 2 2 0 = −  − = e dr a d r r a  ∴ a0 r = 是最可几半径。 (4) 2 2 2 2 ˆ 2 1 ˆ = = −     T p       − −       = − 0 2 0 0 / 2 / 2 3 0 2 [ ( )] sin 1 2 0 0 e e r drd d a T  r a r a     − − = −       0  2 0 0 2 / 2 2 / 3 0 2 [ ( )] sin 1 1 2 0 0 e r drd d dr d r dr d r e a  r a r a   − = − − − 0 / 0 2 0 3 0 2 (2 ) 1 ( 2 4 0 e dr a r r a a r a           +     +      = 2 2 2 2 2 sin 1 (sin ) sin 1 ( ) 1     r   r r r

(⑤)c(p)=「w()w(r,0,p)dr oa动贰成 drdod d-cos 2π 2jharehhel 2π ipr 5owc的h x'e-"dx= a (n为正整数，a心0) 2π 方。1 1 (i( 方p) 1 Aip 2anp元a,i 4 agh √2ah'πa。(a2p2+h2) 、 (2ah)32h z(a2p2+h2)月 动量几率分布函数 8aghs (p)=k(p)=(p 3.3证明氢原子中电子运动所产生的电流密度在球极坐标中的分量是 Jer=Jee=0 Je=chm na加e户 证：电子的电流密度为

4 2 0 2 2 0 2 0 4 0 2 2 ) 4 4 (2 2 4 a a a a    = − = (5) c p  r  r   d p ( ) ( ) ( , , ) *    =     − − =         2 0 0 cos 0 / 2 3 0 3/ 2 sin 1 (2 ) 1 ( ) 0 e r dr e d d a c p pr i r a     = −  − −       0 cos 0 2 / 3 0 3/ 2 ( cos ) (2 ) 2 0 r e dr e d a pr i r a     − − = 0 0 cos 2 / 3 0 3/ 2 0 (2 ) 2      pr i r a e ipr r e dr a      − − = − 0 / 3 0 3/ 2 ( ) (2 ) 2 0 re e e dr a ip pr i pr i r a         + − = 0 1 ! n n ax a n x e dx ( n 为正整数，a>0) ] ) 1 ( 1 ) 1 ( 1 [ (2 ) 2 2 0 2 0 3 0 3/ 2 p i a p i a a ip     + − − =    2 2 2 2 0 0 3 3 0 ) 1 ( 4 2 1    p a a ip a ip + =  2 2 2 2 0 4 4 0 0 3 3 0 2 ( ) 4    + = a p a a  a 2 2 2 2 0 3 / 2 0 ( ) (2 )    + = a p a  动量几率分布函数 2 2 4 0 2 3 5 0 2 ( ) 8 ( ) ( )   + = = a p a p c p   # 3.3 证明氢原子中电子运动所产生的电流密度在球极坐标中的分量是 Jer = Je = 0 2 sin e n m r e m J       = 证：电子的电流密度为

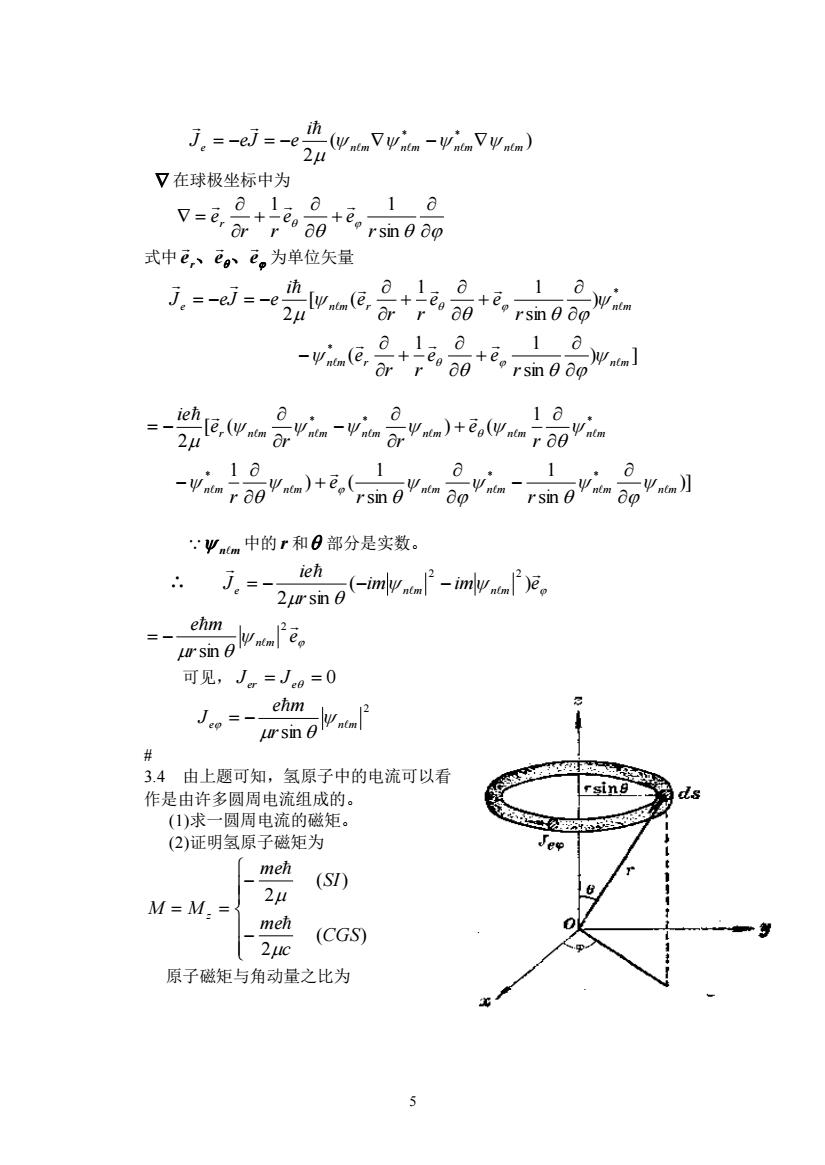
j.=-ej=-eh.@Wz-Yvim-yiwh） 24 又在球极坐标中为 1a rsin 0 do 式中，。，为单位矢量 j。=-ej=-e -Wic(E, -鼎-以景r侧品2 18 vi ro0"a)+,( 品0 Ψm中的r和日部分是实数。 ieh J.=-2ursm0 -imv-imV)e。 ofe 可见，J=J。=0 mgwa 3.4由上题可知，氢原子中的电流可以看 作是由许多圆周电流组成的。 (1)求一圆周电流的磁矩。 (2)证明氢原子磁矩为 meh (S) M=M.= 24 meh 2uc (CGS) 原子磁矩与角动量之比为 5

5 ( ) 2 * * e n m n m n m n m i J eJ e             = − = −  −   在球极坐标中为        +   +    = sin 1 1 r e e r r er    式中   e e e r    、 、 为单位矢量 ) ] sin 1 1 ( ) sin 1 1 [ ( 2 * * n m r n m e n m r n m r e e r r e r e e r r e i J eJ e                               +   +   −   +   +   = − = − )] sin 1 sin 1 ) ( 1 1 [ ( ) ( 2 * * * * * * n m n m n m n m n m n m r n m n m n m n m n m n m r r e r r e r r e ie                                        −   +   −   +   −   = −  nm 中的 r 和  部分是实数。 ∴      im im e r ie Je n m n m      ( ) 2 sin 2 2 = − − −     e r e m n m    2 sin = − 可见， Jer = Je = 0 2 sin e n m r e m J       = − # 3.4 由上题可知，氢原子中的电流可以看 作是由许多圆周电流组成的。 (1)求一圆周电流的磁矩。 (2)证明氢原子磁矩为        − − = = ( ) 2 ( ) 2 CGS c me SI me M M z     原子磁矩与角动量之比为