Chap.4 The representalion for the stetes and dynamical varlable (2)含有连续本征值情况 例如,氢原子能量就是这样一种力学 量,即有分立也有连续本征值。 设力学量Q的本征值和本征函数分别为: Q1,Q23.,Qn.q an(t)= Wn*(x)Ψ(x,t) u(,u2(,u☒,ug( a,()=∫ u。*(x)平(x,t) 平(x,)=∑an(t)4n(x)+∫a,t)4,(x)dg 归一化则变为: ∑n*(t)a(t)+∫a,*(t)a,()dg =1 la.()P是在平(飞,0 态中测量力学量 1a,2d是在平(x,t)态中测量力学量 Q所得结果为Q。 a,(t) Q所得结果在q→q+dq之间的几率。 的几率; a2(t) 平 Ψ=4,()* 42())* 0n()* a,()* 在这样的表象中,Ψ a (t) 仍可以用一个列矩阵 归一化仍可表为:平+Ψ=1 表示: a(t) 11
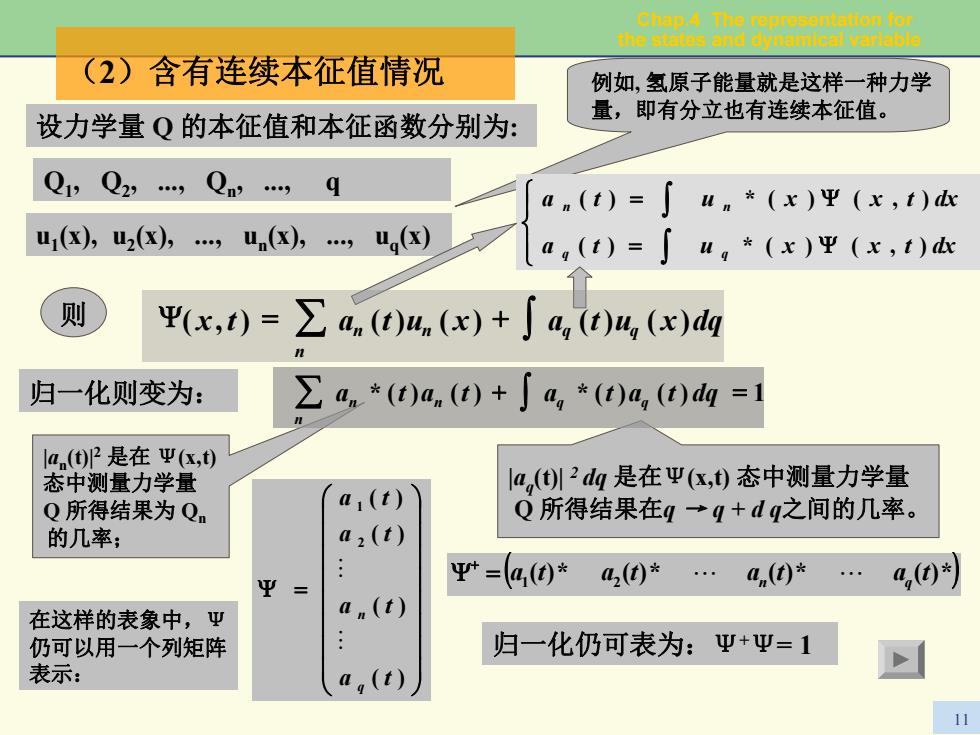
Chap.4 The representation for the states and dynamical variable 11 ( 2)含有连续本征值情况 例如, 氢原子能量就是这样一种力学 量,即有分立也有连续本征值。 设力学量 Q 的本征值和本征函数分别为: Q 1, Q 2, ., Q n, ., q u 1(x), u 2(x), ., u n(x), ., u q(x) 则 ⎪ ⎩ ⎪ ⎨ ⎧ = Ψ = Ψ ∫ ∫ a t u x x t dx a t u x x t dx q q n n ( ) * ( ) ( , ) ( ) * ( ) ( , ) 归一化则变为: |a n(t)| 2 是在 Ψ(x,t) 态中测量力学量 Q 所得结果为 Q n 的几率; |a q(t)| 2 dq 是在Ψ(x,t) 态中测量力学量 Q 所得结果在q → q + d q之间的几率。 在这样的表象中,Ψ 仍可以用一个列矩阵 表示: ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ Ψ = ( ) ( ) ( ) ( ) 2 1 a t a t a t a t q n # # ( ( ) * ( ) * ( ) * ( ) * ) 1 2 a t a t a t a t Ψ = " n " q + 归一化仍可表为:Ψ + Ψ= 1 x t a n t un x a q t uq x dq n Ψ ( , ) = ∑ ( ) ( ) + ∫ ( ) ( ) ∑ a n * ( t ) a n ( t ) + ∫ a q * ( t ) a q ( t ) dq = 1 n

Chap.4 The representation for the states and dynamical varlable 同一状态可以在不同表象用波函数描写,表象不同, (三)讨论 波函数的形式也不同,但是它们描写同一状态。 坐标表象 动量表象 动量本征 (x,t)=[1/(]expli(p'x-E't)/] C(p,t)=8 (p'-p)expl-iE't/] 函数 不含时间 中,(x)=[1/(2π]2 exp[ip'x/h例 C(p)=δ(p'-p) 的动量本 征函数 本征方程p)=p'中) pδ(p'-p)=p'δ(p'-p) 这类似于一个矢量可以在不同坐标系描写一样。矢量A在直角坐标系由 三分量AAA,描述;在球坐标系用三分量AA。A。描述。A、A,A,和Ar, A,A。形式不同,但描写同一矢量A。 12
Chap.4 The representation for the states and dynamical variable 12 这类似于一个矢量可以在不同坐标系描写一样。矢量 A在直角坐标系由 三分量Ax Ay Az 描述;在球坐标系用三分量Ar Aθ Aϕ 描述。 Ax Ay Az和 Ar, Aθ, Aϕ 形式不同,但描写同一矢量A。 同一状态可以在不同表象用波函数描写, 表象不同, 波函数的形式也不同, 但是它们描写同一状态。 (三)讨论 坐标表象 动量表象 动量本征 函数 Ψp'(x,t)=[1/(2π=)]1/2exp[i(p'x-E't)/=] C(p,t)=δ(p'-p)exp[-iE't/=] 不含时间 的动量本 征函数 ψp'(x)= [1/(2π=)]1/2 exp[ip'x/=] C(p)=δ(p'-p) 本征方程 p ψp'(x)=p'ψp'(x) pδ(p'-p)=p'δ(p'-p)

Chap.A The representslion for the states and dynamical varlable 量子力学表象 坐标系 基本矢量 不同表象波函数 不同坐标系的一组分量 u1(x),2(x),.,u(x),. i,j,k, a1(t),a2(t),an(t), Ax Ar:Aa 量子状态Ψ(x,t) 矢量A 态矢量 所以我们可以把状态平看成是一个矢量 一一态矢量。 选取一个特定力学量Q表象,相当于选取特定的坐标系, u1(x),u2(x),., u(x), 。 是Q表象的基本矢量简称基矢。 13
Chap.4 The representation for the states and dynamical variable 13 量子力学 表象 坐标系 不同表象波函数 不同坐标系的一组分量 u1(x), u2(x),., un(x), . i, j, k, a1(t), a2(t),., an(t), . Ax, Ay, Az 量子状态Ψ(x,t) → 矢量 A 态矢量 基本矢量 所以我们可以把状态Ψ看成是一个矢量——态矢量。 选取一个特定力学量 Q 表象,相当于选取特定的坐标系, u1(x), u2(x), ., un(x), . 是 Q 表象的基本矢量简称基矢

Chap.4 The representstion for the states and dynamical varlable 波函数 a(t) a2(t) 是态矢量Ψ在Q表象中沿各基矢方向上的 平 “分量”。Q表象的基矢有无限多个,所以 : 态矢量所在的空间是一个无限维的抽象的 a (t) 函数空间,称为Hilbert空间。 §2算符的矩阵表示 (一)力学量算符的矩阵表示 (二)Q表象中力学量算符F的性质 (三)Q有连续本征值的情况 14
Chap.4 The representation for the states and dynamical variable 14 波函数 ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ =Ψ ## )( )( )( 21 ta ta ta n 是态矢量Ψ在Q表象中沿各基矢方向上的 “分量”。Q表象的基矢有无限多个,所以 态矢量所在的空间是一个无限维的抽象的 函数空间,称为Hilbert空间。 (一)力学量算符的矩阵表示 (二)Q 表象中力学量算符 F 的性质 (三)Q 有连续本征值的情况 §2算符的矩阵表示
Chap.A The representslion for the states and dynamical varlable (一)力学量算符的矩阵表示 坐标表象: Q表象: 假设只有分立本征值,将 中,平按{u(x)}展开: (x,t)=F(x,p)Ψ(化,t) 代入 Ψ(x,0=Σ am(t)um(x) =F(x,-ih悬)Ψ(x,) Φ(x,t)=∑ b(t)um(x) 两边左乘u*心) ∑bn()unm(x)=F(x,-i品)∑an()um(x) 并对x积分 m ∑bn()jun*un(c)dk=∑刂un*f(x,-ii悬)n(x)clan() ∑bn(d)m=∑Fnmn( b.(0)=∑Fnn Q表象的 表达方式 Fnm=∫n*(x)F(,-ih)unm(x)d 15
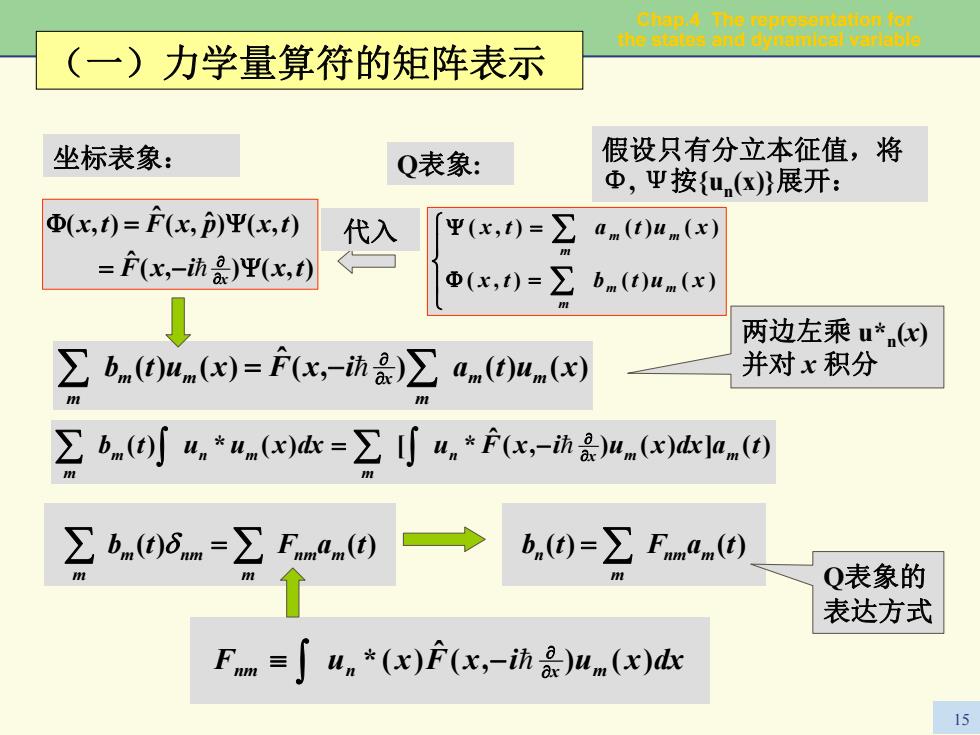
Chap.4 The representation for the states and dynamical variable 15 坐标表象: ),(),( ˆ ,( ˆ ),() ˆ ),( txixF txpxFtx x Ψ−= Ψ=Φ ∂ ∂ = Q表象: 假设只有分立本征值,将 Φ, Ψ按{un(x)}展开: ⎪⎩ ⎪⎨⎧ =Φ =Ψ ∑∑ ),( )()( ),( )()( xutbtx xutatx m m m m m m )()(),( ˆ )()( mm xutaixFxutb m mm x m ∑ ∂ ∑∂ −= = 两边左乘 u*n(x) 并对 x 积分 )(])(),( ˆ dxxuutb *[)(*)( m m tadxxuixFun x m m mn m ∂ ∂ = − ∑ ∫ ∑ ∫ = tb )( taF )( mnm m nmm m δ = ∑∑ )( taFtb )( mnm m n = ∑ nm n )(* ˆ ∂x m )(),( dxxuixFxuF ∂ ≡ − ∫ = Q表象的 表达方式 代入 (一)力学量算符的矩阵表示