
Chap.4 The representstion for the states and dynamical varlable C(p,)的物理意义 1平c,2dx是在Ψc,)所描写的状态中,测量粒子的位 置所得结果在→x+dx范围内的几率。 C(①,)2dp是在Ψ(x,)所描写的状态中,测量粒子的动量所 得结果在p→p+dp范围内的几率。 平c,)与Cp,)一一对应,描述同一状态。ΨK,)是该状态在坐标表象 中的波函数;而C(P,)就是该状态在动量表象中的波函数。 若平(x,t)描写的态是具有确定 平(x,t)=yp(x)eiEA 动量p’的自由粒子态,即: 24
Chap.4 The representation for the states and dynamical variable 6 |C(p,t)| 2 d p 是在Ψ(x,t)所描写的状态中,测量粒子的动量所 得结果在 p → p + d p 范围内的几率。 |Ψ(x,t)| 2d x 是在Ψ(x,t)所描写的状态中,测量粒子的位 置所得结果在 x → x + d x 范围内的几率。 Ψ(x,t) 与 C(p,t) 一 一 对应,描述同一状态。Ψ(x,t)是该状态在坐标表象 中的波函数;而C(p,t) 就是该状态在动量表象中的波函数。 C(p,t)的物理意义 若Ψ(x,t) 描写的态是具有确定 动量 p’ 的自由粒子态,即: μ ψ 2 )(),( 2 / p E extx p tiE p p ′ = =Ψ ′ − ′ ′ =
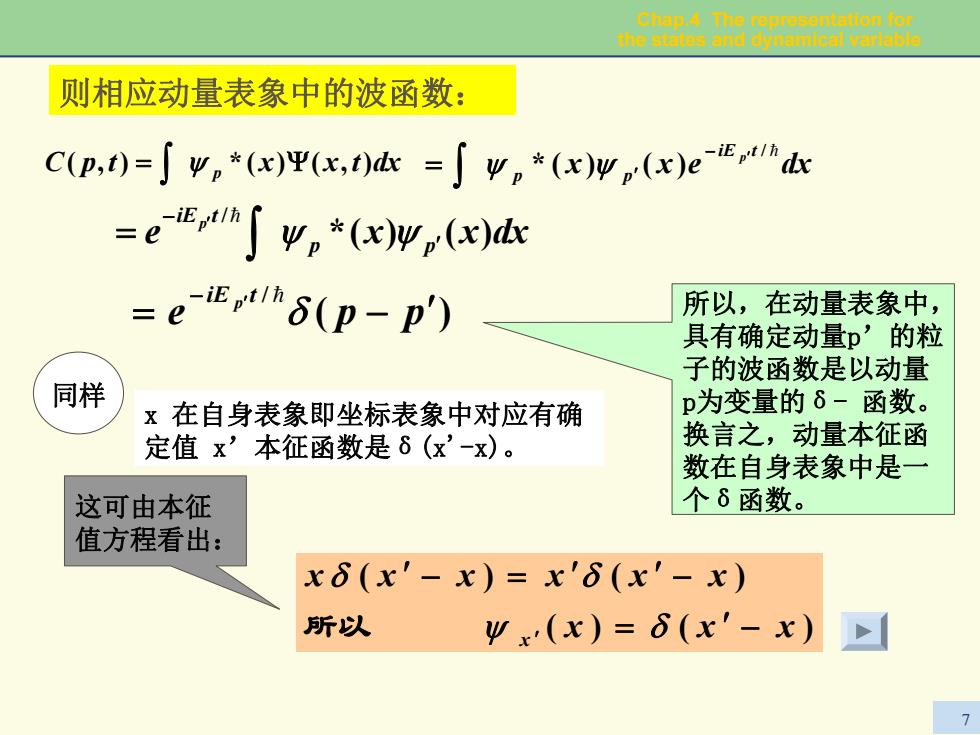
Chap.A The representsllon for the states and dynamical varlable 则相应动量表象中的波函数: C(p,)=∫9,*(x)平(x,t)=∫y。*(x)yn(x)ed在 =eem∫g,*(xwn(x) =e-i(p-p') 所以,在动量表象中, 具有确定动量p’的粒 子的波函数是以动量 同样 x在自身表象即坐标表象中对应有确 p为变量的6-函数。 定值x’本征函数是6(x-x)。 换言之,动量本征函 数在自身表象中是一 这可由本征 个6函数。 值方程看出: x6(x'-x)=x'6(x'-x) 所以 Ψx(x)=6(x'-x) 7
Chap.4 The representation for the states and dynamical variable 7 e dxxx p p p tiE )()(* / ′ − ∫ ′ = ψψ = )( / ppe p tiE = − ′ − ′ δ= 所以,在动量表象中, 具有确定动量p’的粒 子的波函数是以动量 p为变量的δ- 函数。 换言之,动量本征函 数在自身表象中是一 个δ函数。 x 在自身表象即坐标表象中对应有确 定值 x’本征函数是δ(x'-x)。 同样 这可由本征 值方程看出: )()( )()( xxx xxxxxx x = ′ − ′ − = ′ ′ − ψ ′ δ δ δ 所以 则相应动量表象中的波函数: tpC dxtxx p = Ψ ),()(*),( ∫ ψ dxexx tiE p p p / = )()(* − ′ = ∫ ψψ ′

Chap.4 The representstion for the states and dynamical varlable (二)力学量表象 推广上述讨论: x,p都是力学量,分别对应有坐标表象和动量表象, 因此可以对任何力学量Q都建立一种表象,称为力学量Q表象. 问题 那末,在任一力学量Q表象中,平(x,t)所描写的态又如何表示呢? (1)具有分立本征值的情况 (2)含有连续本征值情况
Chap.4 The representation for the states and dynamical variable 8 那末,在任一力学量Q表象中,Ψ(x,t)所描写的态又如何表示呢? 推广上述讨论: x, p 都是力学量,分别对应有坐标表象和动量表象, 因此可以对任何力学量Q都建立一种表象,称为力学量 Q 表象. 问题 (1)具有分立本征值的情况 (2)含有连续本征值情况 (二)力学量表象
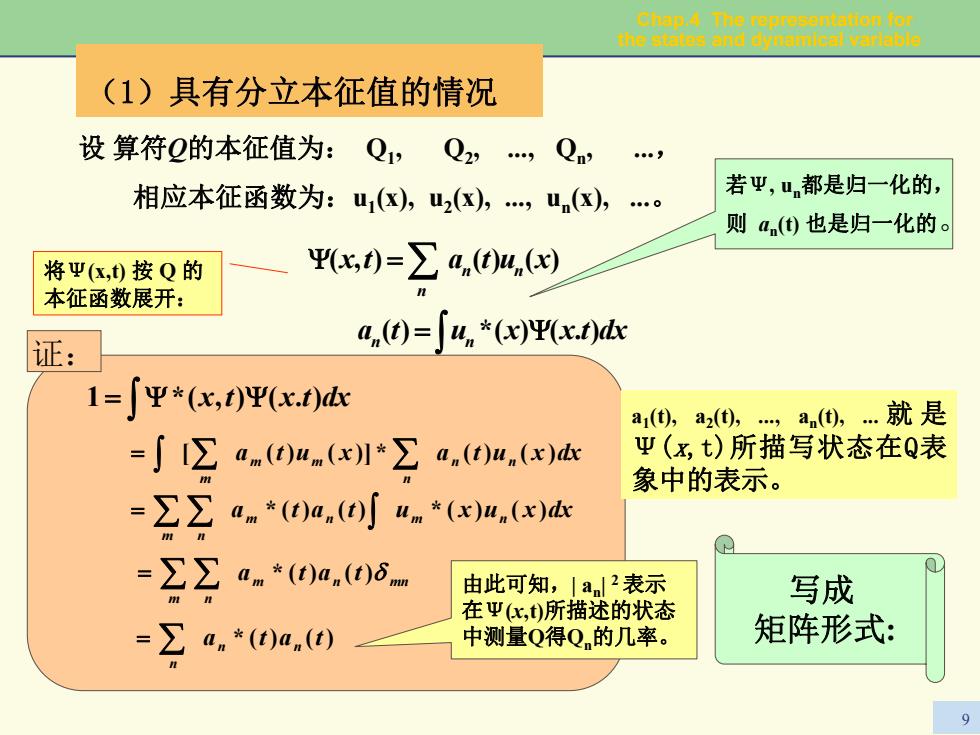
Chap.A The representstlon for the states and dynamical varlable (1)具有分立本征值的情况 设算符Q的本征值为:Q1,Q2,Q, 相应本征函数为:u1(),u2(),(, 若平,u都是归一化的, 0 则a)也是归一化的。 将平(k,)按Q的 x0=∑a.④u,y 本征函数展开: 证: a.0=∫4,*wxf) 1=∫平*(x,)Ψ(x.t)d a1(),a20,an(,.就是 =∫[∑an0un(x川*∑a,(0u,(x) Ψ(x,t)所描写状态在Q表 象中的表示。 =Σa.a.o”.*(xu.(e =22a.*0a,06 由此可知,|a2表示 写成 在Ψ(c,)所描述的状态 =2a.a.@ 中测量Q得Q的几率。 矩阵形式:
Chap.4 The representation for the states and dynamical variable 9 (1)具有分立本征值的情况 设 算符Q的本征值为: Q1, Q2, ., Qn, ., 相应本征函数为:u1(x), u2(x), ., un(x), .。 将Ψ(x,t) 按 Q 的 本征函数展开: ∫ ∑ Ψ= =Ψ dxtxxuta xutatx n n nn n ).()(*)( )()(),( 若Ψ, un都是归一化的, 则 an(t) 也是归一化的。 ∫ ΨΨ= ).(),(*1 dxtxtx 证: dxxutaxuta nn n m m m ∑ ∑ )()(*)]()([ ∫ = m n m n dxxuxutata m n )()(*)()(* ∑ ∑ ∫ = m n mn m n = ∑ ∑ tata )()(* δ tata )()(* n n n = ∑ 由此可知,| an| 2 表示 在Ψ(x,t)所描述的状态 中测量Q得Qn的几率。 a1(t), a2(t), ., an(t), . 就 是 Ψ(x,t)所描写状态在Q表 象中的表示。 写成 矩阵形式:

Chap.4 The representstion for the states and dynamical varlable 41(t) 共轭矩阵 a2(t) Ψ= 平=(4,))*☑()*.n()*. a (t) 归一化可写为 a1(t) u2(t) 平+Ψ=(a,(t)* a2(t)*.an(t)* .) a (t) =∑a()*a.(0=1 10
Chap.4 The representation for the states and dynamical variable 10 ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ =Ψ ## )( )( )(21 ta ta tan 共轭矩阵 ( *)(*)( " *)( ") 1 2 =Ψ tata n ta + 归一化可写为 ( ) 1)(*)( )( )( )( *)(*)( *)( 2 1 1 2 = = ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ =ΨΨ ∑ + tata ta ta ta tata ta n n n n n # " #