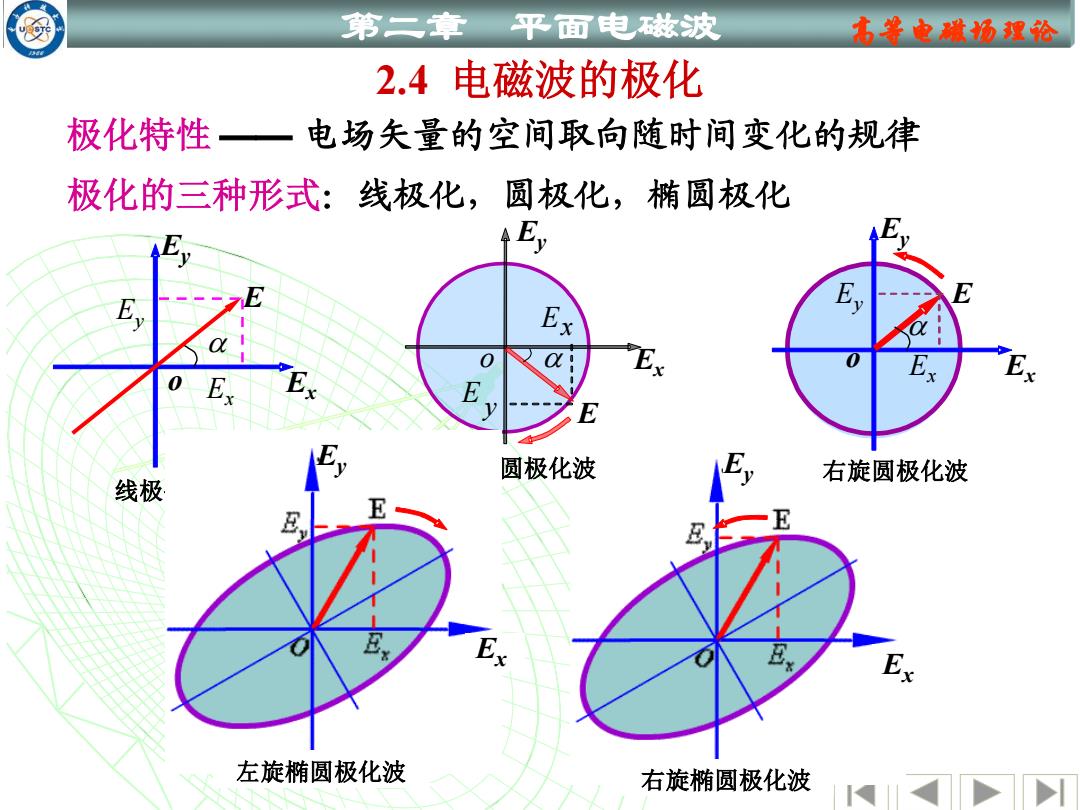
第二章 平面电磁波 古等电蠟场理论 2.4电磁波的极化 极化特性一 电场失量的空间取向随时间变化的规律 极化的三种形式:线极化,圆极化,椭圆极化 E Ex 圆极化波 右旋圆极化波 线极 左旋椭圆极化波 右旋椭圆极化波
第二章 平面电磁波 高等电磁场理论 2.4 电磁波的极化 极化特性 —— 电场矢量的空间取向随时间变化的规律 极化的三种形式:线极化,圆极化,椭圆极化 右旋椭圆极化波 Ey Ex 左旋圆极化波 o Ex Ey Ex y E E 右旋圆极化波 o Ex Ey Ex Ey E 线极化波 o Ex Ey Ex E Ey 左旋椭圆极化波 Ex Ey

第二章 平面电滋波 古等电蠟场理论 极化的三要素:强度,椭圆度,旋转特性 极化的描述方式一三个独立参数
第二章 平面电磁波 高等电磁场理论 极化的三要素:强度,椭圆度,旋转特性 极化的描述方式 —— 三个独立参数

第二章 平面电滋波 名等电城场望论 (1)振幅Ex0E,o和相位差专 E=Exo cos@t E,=Eyo cos(ot+) E2 E E,E,cos5=1 Ezo sin2 Eo sin2 ExoEyo sin Exo Exo 强度,E0/Exo—椭圆度,、 —旋转特性 5=0,π 一线极化 Ex0=E0,5=±π/2 圆极化 5≠0,π或E0≠E,0,5=士/2一椭圆极化 0<5<π一左旋,一π<5<0一右旋;
第二章 平面电磁波 高等电磁场理论 0 0 cos cos( ) x x y y E E t E E t = = + 2 2 2 2 2 2 2 0 0 0 0 cos 1 sin sin sin x y x y x y x y E E E E E E E E + − = (1) 振幅 E x0 、 E y 0 和相位差 0 0 0, π , π 2 0, π E E x y = = = 0 0 , π 2 E E x y 或 = ——线极化 ——圆极化 ——椭圆极化 E x0 、E y 0 ——强度, E E y x 0 0 ——椭圆度, ——旋转特性 0 π ——左旋,− π 0 ——右旋;

第二章 平面电滋波 古等电赋场望论 (2)长半轴OA、短半轴OB和取向角T 0A2+OB2=E+E30 2ExoEyo tan 27 B E-E刘 cos (0≤t≤π) sin2x= 2ExoEyo sing Eo+Eo 其中:x=tan(±OB/OA) 一椭圆率角 (-π/4≤x≤π/4)
第二章 平面电磁波 高等电磁场理论 (2)长半轴 OA 、短半轴 OB 和取向角 2 2 2 2 OA OB E E + = + x y 0 0 0 0 2 2 0 0 2 tan 2 cos x y x y E E E E = − 0 0 2 2 0 0 2 sin 2 sin x y x y E E E E = + 其中: 1 tan ( ) OB OA − = —— 椭圆率角 (− π 4 π 4) (0 π)

第二章 平面电滋波 名等电斌场理论 (3)斯托克斯极化参量S、S1、S2、S? 定义: S。=E+E 0S,=E-E30 S2=2Ex0Eyo cos S3 =2ExoEyo sin 斯托克斯极化参量S、S,、S2、S3是强度的二次式,表征 极化状态更方便。 例:①S?=0→Eo=0或E0=0或5=0,π→线极化 ②S1=S2=0→Ex0=E,05=±π/2→圆极化 若S3>0→5=π/2→ 左旋圆极化 S,<0→5=-π/2→右旋圆极化
第二章 平面电磁波 高等电磁场理论 ( 3 )斯托克斯极化参量 S0 、S1 、S2 、S3 定义: 2 2 0 0 0 x y S E E = + 2 2 1 0 0 x y S E E = − 2 0 0 2 cos x y S E E = 3 0 0 2 sin x y S E E = 斯托克斯极化参量 S0 、S1 、S2 、S3 是强度的二次式,表征 极化状态更方便。 例:① 3 S = 0 1 2 ② S S = = 0 3 S 0 圆极化 3 若 S 0 线极化 E E x y 0 0 = = 2 0 0 E x = 或 0 0 E y = 或 = 0, 左旋圆极化 右旋圆极化 = 2 = − 2