电子科技大学：《高等电磁场理论》课程教学资源（课件讲稿）第二章 平面电磁波

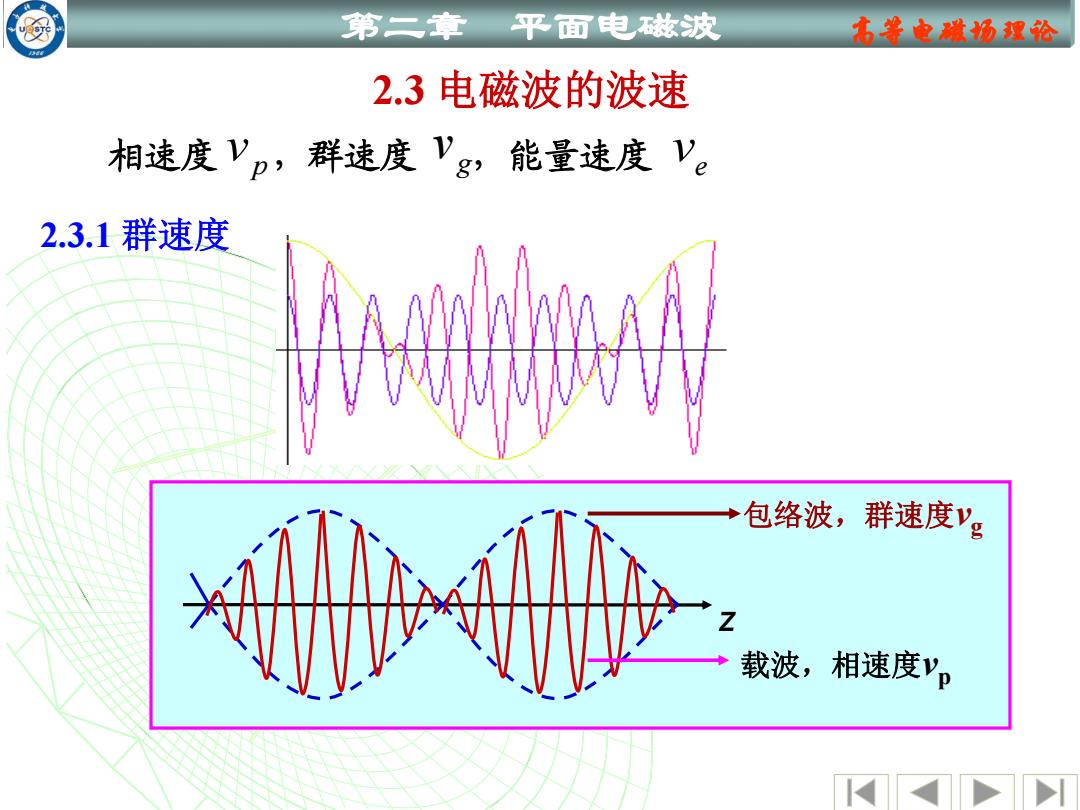
第二章 平面电滋波 名等电城场望论 2.3电磁波的波速 相速度Vp,群速度Vg,能量速度Ve 2.3.1群速度 A 包络波，群速度Vg ☑ 载波，相速度Vp

第二章 平面电磁波 高等电磁场理论 2.3 电磁波的波速 相速度 v p ，群速度 ，能量速度 e v g v 2.3.1 群速度 z 载波，相速度vp 包络波，群速度vg

第二章 平面电效波 古等电蠟场理论 00 一中心频率 窄带信号：0∈(@-60，o,+60）（0一频带宽度 0o+6o 则E(r,)=∫E(o)ex(-kd@ 00-6o 由于 6o=a)+ga-a ot-k·r≈0t-k(oo)r+(0-0)t- ak(o】.r] ∂0 00+6o →E(r,t)=eo-or)∫ E(a)e 00-6w 0e ok →g=e:k, 00 00( 0 +e冰 ak

第二章 平面电磁波 高等电磁场理论 0 0 ( ) ( , ) ( )e d j t t        + −  − =  k r 则 E r E 0 0 0 ( ) ( ) ( ) ( )         = + − +  k 由于 k k 0 0 0 0 0 ( ) t t t ( ) ( )[ ]          −   −  + − −   k k r k r r 0 0 0 0 0 0 ( )[ ] ( ) ( , ) e ( )e d j t j t t           +  − −   −  −  =  k r k r E r E 0 0 窄带信号：       − + ( , ) 0 ——中心频率  ——频带宽度 （ ） g x y z x y z k k k         = + + =      v e e e k

第二章 平面电滋波 名等电城场望论 ★群速度与相速度的关系 d N do dk dk (,k)=p+k dk 二Vp dvpd@=vp+ dvp vp do dk do V o dv 1 p do dvpd0<0→vg<'p(正常色散) →dv,/d0>0→Vg>vp(反常色散) dvp/d0=0户yg=yp(非色散)

第二章 平面电磁波 高等电磁场理论 d d ( ) d d g p v v k k k  = = d 1 d p g p p v v v v    = − ★ 群速度与相速度的关系 d d d d p p p v v v k    = + d d 0 d d 0 d d 0 p g p p g p p g p v v v v v v v v v                = =  （反常色散） （正常色散） （非色散） d d p p v v k k = + d d p p g p v v v v   = +

第二章 平面电滋波 古等电蠟场理论 2.3.2能速 S 定义：V。= v av 其中：Sm=Re(E×H*) "E+5 在非色散媒质中Ve=Vg=Vp 在色散媒质中一般不相同

第二章 平面电磁波 高等电磁场理论 1 1 2 2 2 2 w av = +     E H Re( ) av  其中： S E H =  在色散媒质中一般不相同。 2.3.2 能速 av e w av = S 定义： v 在非色散媒质中 v v v e g p = =

第二章 平面电滋波 名等电城场理论 【例】 导电媒质相速度y。、群速度”与能量速度。 E=Eoe-ae--H=+i -e.x Ee-a-e-iB= jou a=m+品-=受气-品+ 2v do_22V1+(/oe) 令V= B [W+(G/oc)2+1a, dB [V1+(o/o)2+1]/2 wf ew(aloeY EoPe sEH水Rf。 a √2v Weay+Wmav [V1+(o/o8)2+1]

第二章 平面电磁波 高等电磁场理论 【例】 导电媒质相速度vp、群速度 vg 与能量速度ve 0 0 e e , e e z j z z j z z j j         − − − − + E E H e E = =  2 1 2 2 1 2 [ 1 ( ) 1] , [ 1 ( ) 1] 2 2           = + − = + + 2 p g 2 1 2 2 3 2 2 d 2 2 1 ( ) , [ 1 ( ) 1] [ 1 ( ) 1] d v v v v            + = = = = + + + + 2 2 av 0 1 Re( ) e 2 2   z    − S E H E =  = 2 2 2 2 2 eav 0 mav 0 1 1 e , 1 ( ) e 4 4 4 4 z z w w          −  − =  =  + E E E H H E = = av e 2 1 2 eav mav 2 [ 1 ( ) 1] v v w w   = = + +  + S