
3.2 Sparsity Rendering Algorithms From the above answers. m lnal,2S≤rank(Φ),so for中,at mostΦ∈Rmxm,at most号sparse vector can be guaranteed to be recovered. Specially,a Gaussian random matrix (each element is independently generated from normal distribution)satisfies with a overwhelming probability the requisition mentioned by the lemma. In many situations,there exists noise,so it is of more interest to solve y=Φw+e
3.2 Sparsity Rendering Algorithms From the above answers. In all, , so for , at most , at most sparse vector can be guaranteed to be recovered. Specially, a Gaussian random matrix (each element is independently generated from normal distribution) satisfies with a overwhelming probability the requisition mentioned by the lemma. In many situations, there exists noise, so it is of more interest to solve
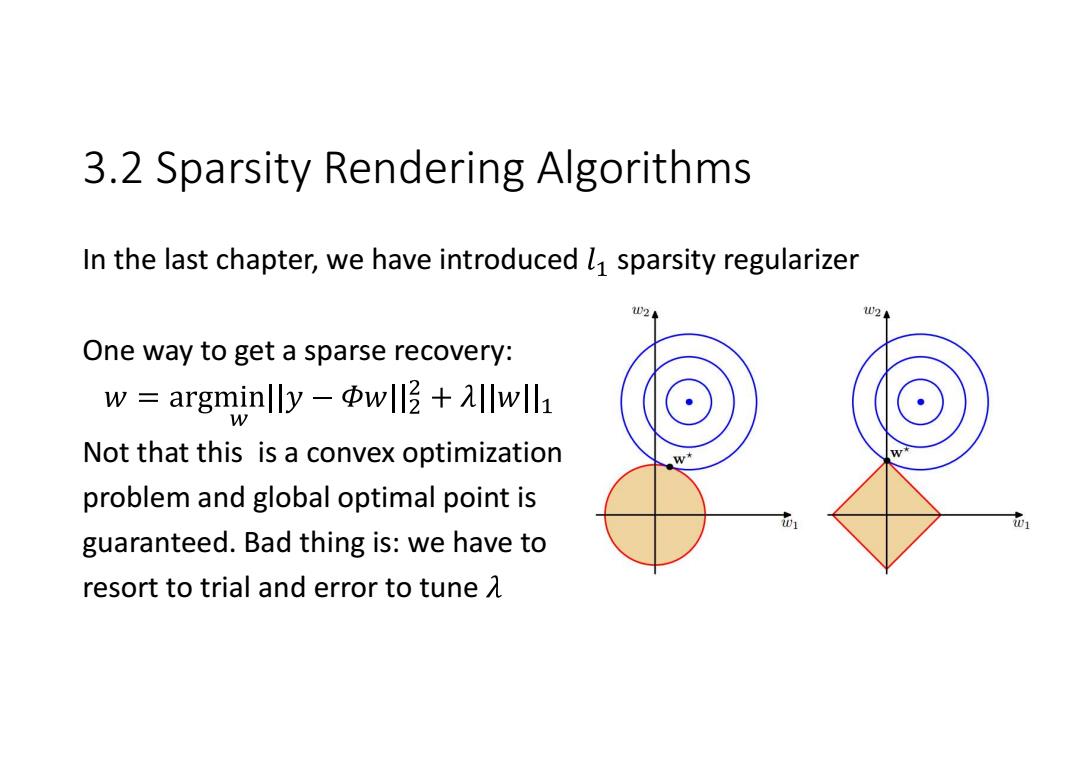
3.2 Sparsity Rendering Algorithms In the last chapter,we have introduced l sparsity regularizer D2 One way to get a sparse recovery: w argminlly -w+w Not that this is a convex optimization problem and global optimal point is 1 guaranteed.Bad thing is:we have to resort to trial and error to tune a
3.2 Sparsity Rendering Algorithms In the last chapter, we have introduced sparsity regularizer One way to get a sparse recovery: Not that this is a convex optimization problem and global optimal point is guaranteed. Bad thing is: we have to resort to trial and error to tune

3.2 Sparsity Rendering Algorithms Basis Pursuit(BP)is such a l1 regularizer optimization algorithm for the sparse signal recovery problem.It assumes that no noise is present,so the optimization function is: minwwll subject to y w. With some rearranging,this problem can be treated as a linear programming problem
3.2 Sparsity Rendering Algorithms Basis Pursuit (BP) is such a regularizer optimization algorithm for the sparse signal recovery problem. It assumes that no noise is present, so the optimization function is: With some rearranging, this problem can be treated as a linear programming problem

3.2 Sparsity Rendering Algorithms As a matter of fact,to render the recovery sparse,we need to well regularize the solution.In the previous chapters,we have mentioned two ways to add regularization:1 norm regularizer as in BP.2 Bayesian prior. By adopting an appropriate prior for w,the solution for y =w +e may as well be rendered sparse
3.2 Sparsity Rendering Algorithms As a matter of fact, to render the recovery sparse, we need to well regularize the solution. In the previous chapters, we have mentioned two ways to add regularization: 1 norm regularizer as in BP. 2 Bayesian prior. By adopting an appropriate prior for , the solution for may as well be rendered sparse

3.2.1 Sparse Bayesian Learning lny=中w+e,Φ∈Rmxn,y∈Rm,w∈Rn,e∈Rm we suppose each element of e is independently distributed and ei~N(eil0,B-1)= xphereis the variance,writing in this form is to facilitate later computation. Now,to promote sparsity,we add the prior distribution for wi. ww(w0,)=烹exp(-)
3.2.1 Sparse Bayesian Learning In , , , , we suppose each element of is independently distributed and భ మ మ , here is the variance, writing in this form is to facilitate later computation. Now, to promote sparsity, we add the prior distribution for . భ మ మ