
3.1极大似然 ·似然函数:关于统计模型中参数的函数,表示模型参数中的似然性(“似然 性“与”概率”意思相近) ·极大似然:最大可能 ·通常:已知条件结果;极大似然:已知结果→条件(估计值) ·已知样本A,未知参数B: P(A B)P(B) P(BA)= P(A) ·一般步骤: ①写出似然函数并取对数 ②求导数令其为0,得到似然方程 ③解似然方程,得到参数(估计值)
3.1 极大似然 • 似然函数:关于统计模型中参数的函数,表示模型参数中的似然性(“似然 性“与”概率”意思相近) • 极大似然:最大可能 • 通常:已知条件→结果;极大似然:已知结果→条件(估计值) • 已知样本A,未知参数B: • 一般步骤: ① 写出似然函数并取对数 ② 求导数令其为0,得到似然方程 ③ 解似然方程,得到参数(估计值)

3.2隐变量 ·举例:统计学生身高分布 ·样本:100个男生/女生的身高 ·假定:男生和女生身高分别服从相互的独立正态分布,其参数未知 ·已知样本身高的性别:简单的极大似然估计参数 ·未知样本身高的性别:参数估计困难;性别作为隐变量
3.2 隐变量 • 举例:统计学生身高分布 • 样本:100个男生/女生的身高 • 假定:男生和女生身高分别服从相互的独立正态分布,其参数未知 • 已知样本身高的性别:简单的极大似然估计参数 • 未知样本身高的性别:参数估计困难;性别作为隐变量
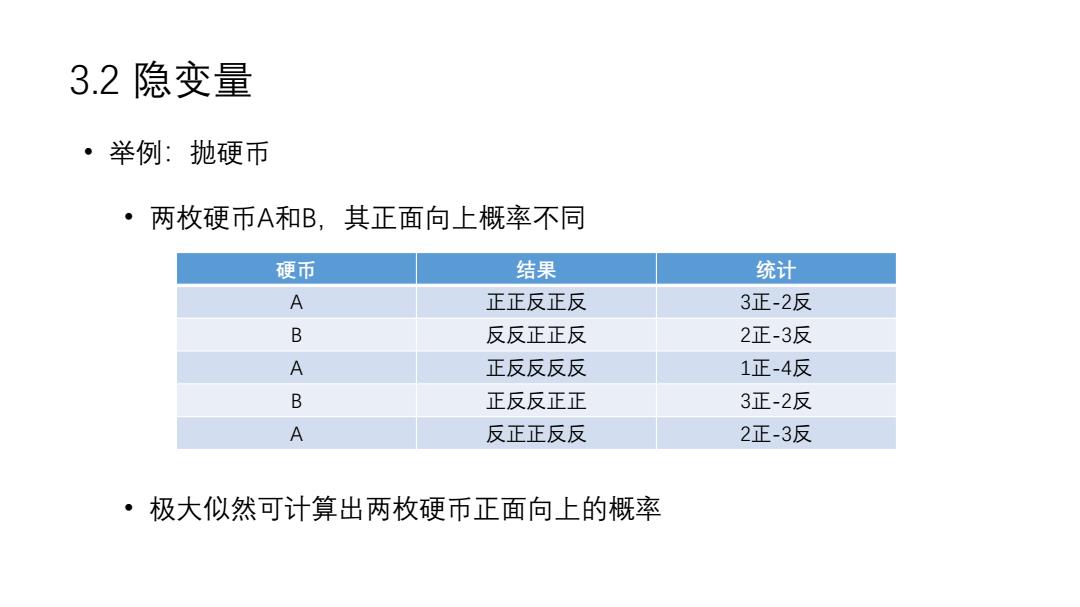
3.2隐变量 ·举例:抛硬币 ·两枚硬币A和B,其正面向上概率不同 硬币 结果 统计 A 正正反正反 3正-2反 B 反反正正反 2正-3反 A 正反反反反 1正-4反 B 正反反正正 3正-2反 A 反正正反反 2正-3反 ·极大似然可计算出两枚硬币正面向上的概率
3.2 隐变量 • 举例:抛硬币 • 两枚硬币A和B,其正面向上概率不同 • 极大似然可计算出两枚硬币正面向上的概率 硬币 结果 统计 A 正正反正反 3正-2反 B 反反正正反 2正-3反 A 正反反反反 1正-4反 B 正反反正正 3正-2反 A 反正正反反 2正-3反
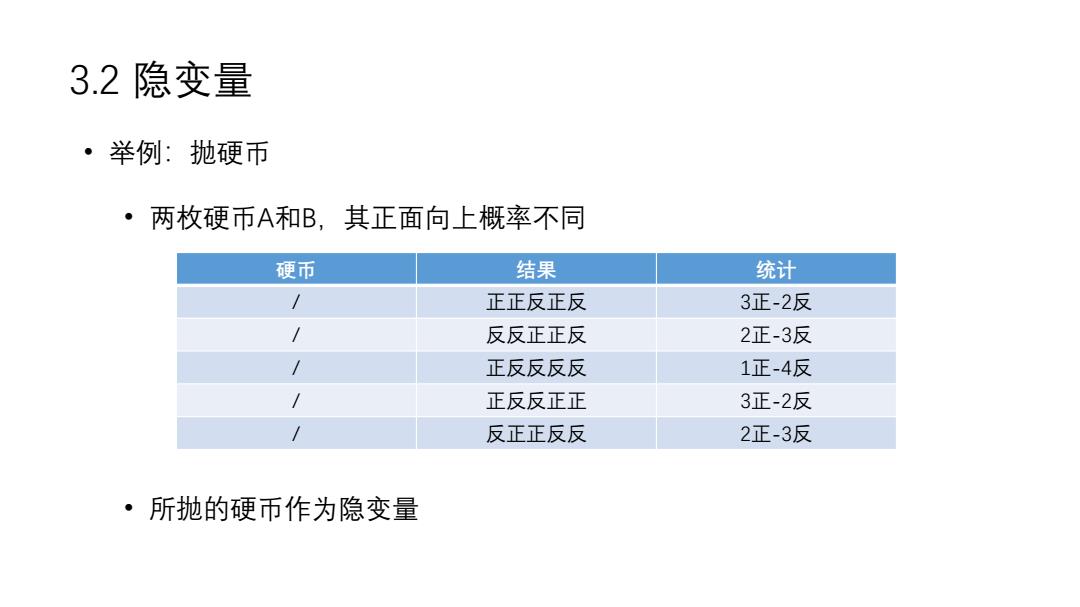
3.2隐变量 ·举例:抛硬币 ·两枚硬币A和B,其正面向上概率不同 硬币 结果 统计 正正反正反 3正-2反 反反正正反 2正-3反 正反反反反 1正-4反 正反反正正 3正-2反 反正正反反 2正-3反 ·所抛的硬币作为隐变量
3.2 隐变量 • 举例:抛硬币 • 两枚硬币A和B,其正面向上概率不同 • 所抛的硬币作为隐变量 硬币 结果 统计 / 正正反正反 3正-2反 / 反反正正反 2正-3反 / 正反反反反 1正-4反 / 正反反正正 3正-2反 / 反正正反反 2正-3反
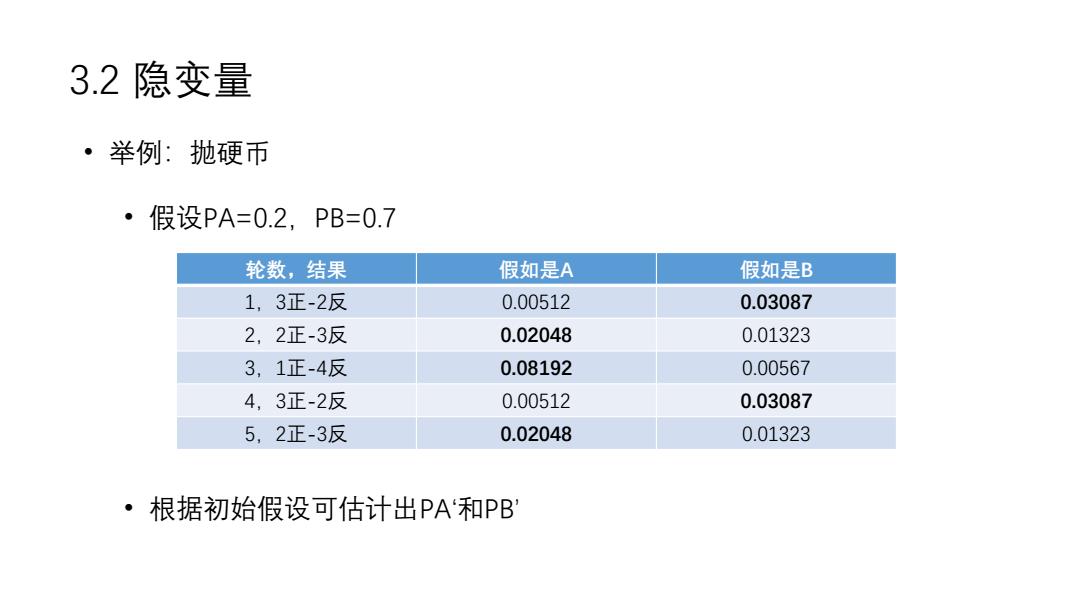
3.2隐变量 ·举例:抛硬币 ·假设PA=0.2,PB=0.7 轮数,结果 假如是A 假如是B 1,3正-2反 0.00512 0.03087 2,2正-3反 0.02048 0.01323 3,1正-4反 0.08192 0.00567 4,3正-2反 0.00512 0.03087 5,2正-3反 0.02048 0.01323 ·根据初始假设可估计出PA‘和PB
3.2 隐变量 • 举例:抛硬币 • 假设PA=0.2,PB=0.7 • 根据初始假设可估计出PA‘和PB’ 轮数,结果 假如是A 假如是B 1,3正-2反 0.00512 0.03087 2,2正-3反 0.02048 0.01323 3,1正-4反 0.08192 0.00567 4,3正-2反 0.00512 0.03087 5,2正-3反 0.02048 0.01323