Solving matching pennies Player 2 Expected Head Tail payoffs Head -1,1 1,-1 r 1-2q Player 1 Tail 1,-1 -1,1 1-x 2g-1 Expected q 1-q payoffs 2r-1 1-2r Player 2's expected payoffs If Player 2 chooses Head,-(1-z)=2-1 If Player 2 chooses Tail,+(-z)=1-2
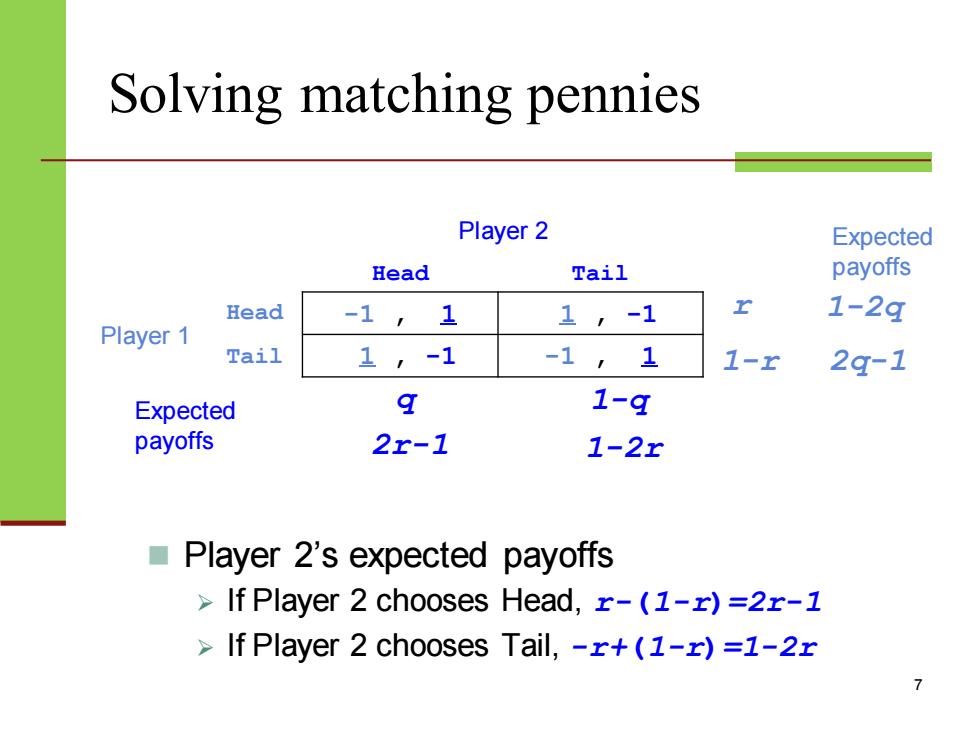
Solving matching pennies Player 2 Head Tail Player 1 Head -1 , 1 1 , -1 Tail 1 , -1 -1 , 1 7 ◼ Player 2’s expected payoffs ➢ If Player 2 chooses Head, r-(1-r)=2r-1 ➢ If Player 2 chooses Tail, -r+(1-r)=1-2r 1-2q 2q-1 Expected payoffs r 1-r Expected q 1-q payoffs 2r-1 1-2r
Solving matching pennies Player 2 Expected Head Tail payoffs Head -1, 1 1,-1 1-2g Player 1 Tail 1,-1 -1,1 1-x 2g-1 Expected q 1-q payoffs 2x-1 1-2x ↑ Player 2's best response B2(r): For r<0.5,Tail (q=0) 1/2 For r>0.5,Head (q=1) For r=0.5,indifferent (0sq<1) 1/2
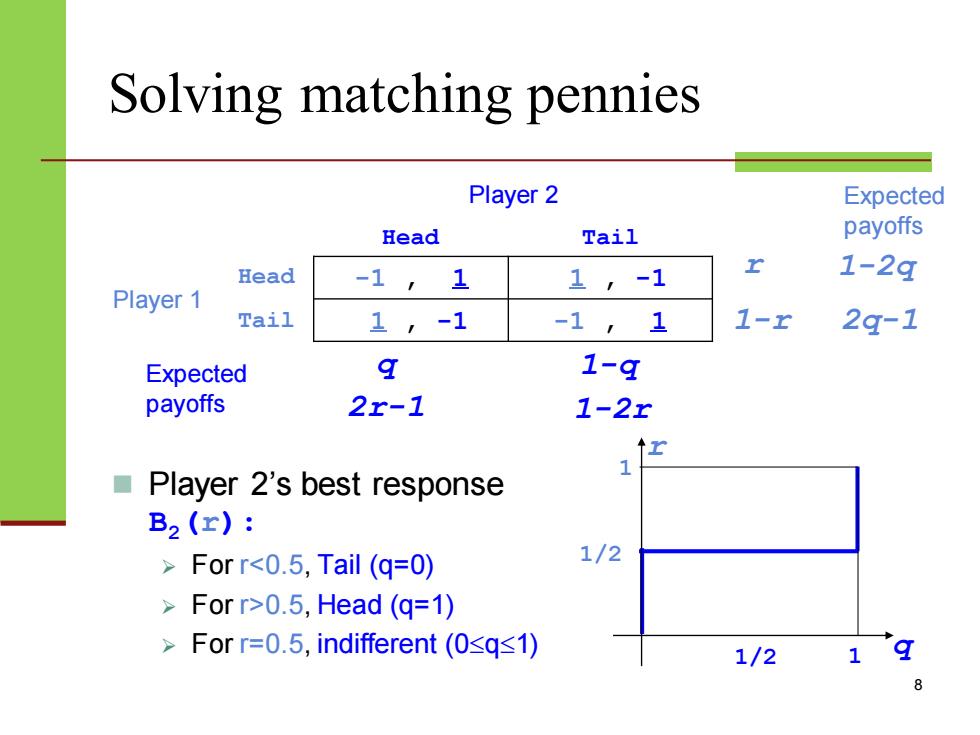
Solving matching pennies Player 2 Head Tail Player 1 Head -1 , 1 1 , -1 Tail 1 , -1 -1 , 1 8 ◼ Player 2’s best response B2(r): ➢ For r<0.5, Tail (q=0) ➢ For r>0.5, Head (q=1) ➢ For r=0.5, indifferent (0q1) q 1-q 1-2q 2q-1 Expected payoffs r 1-r Expected payoffs 2r-1 1-2r 1 q r 1 1/2 1/2
Solving matching pennies Player 2 Head Tail Player 1's best response B1(g): Player Head -1,1 1-1 For q<0.5,Head (r=1)1 Tail 1,-1 -1, 1 1- For q>0.5,Tail (r=0) For q=0.5,indifferent (0srs1) q 1-9 Player 2's best response Mixed strategy B2(r): Nash equilibrium For r<0.5,Tail (q=0) 1 >For r>0.5,Head (q=1) >For r=0.5,indifferent (0sqs1) √Check 12 x=0.5∈B1(0.5) q=0.5∈B2(0.5) 1/2 1 9
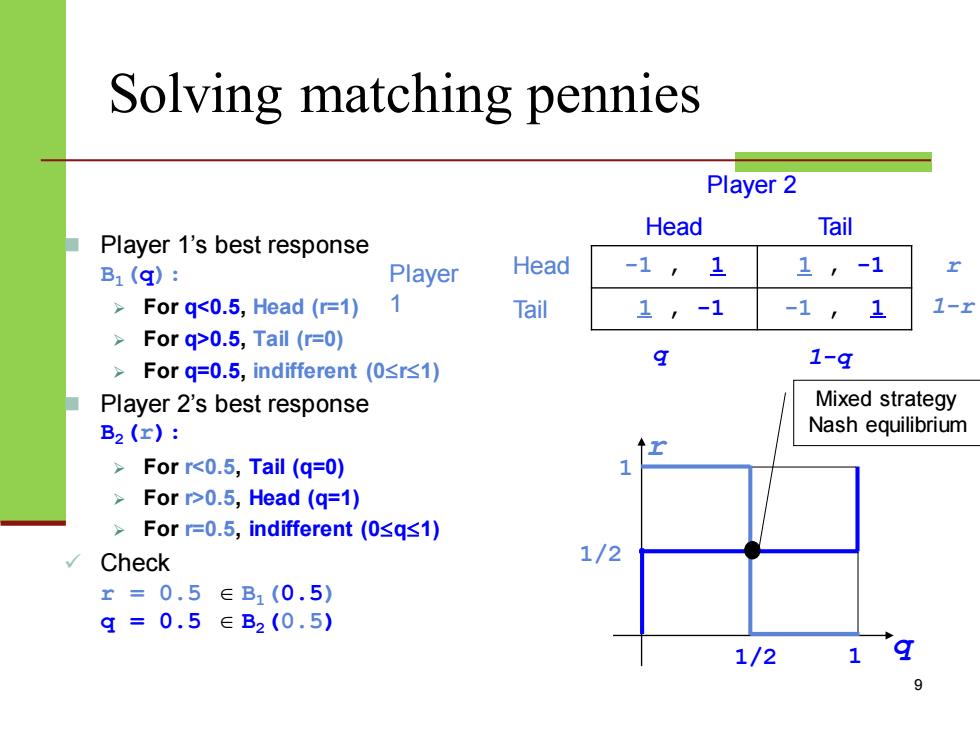
Solving matching pennies Player 2 Head Tail Player 1 Head -1 , 1 1 , -1 Tail 1 , -1 -1 , 1 9 ◼ Player 1’s best response B1(q): ➢ For q<0.5, Head (r=1) ➢ For q>0.5, Tail (r=0) ➢ For q=0.5, indifferent (0r1) ◼ Player 2’s best response B2(r): ➢ For r<0.5, Tail (q=0) ➢ For r>0.5, Head (q=1) ➢ For r=0.5, indifferent (0q1) ✓ Check r = 0.5 B1(0.5) q = 0.5 B2(0.5) 1 q r 1 1/2 1/2 r 1-r q 1-q Mixed strategy Nash equilibrium

Mixed strategy:example Matching pennies Player 1 has two pure strategies:H and T (o(H)=0.5,1(T)=0.5)is a Mixed strategy. That is,player 1 plays H and T with probabilities 0.5 and 0.5,respectively. (1(H)=0.3,1(T)=0.7)is another Mixed strategy. That is,player 1 plays H and T with probabilities 0.3 and 0.7,respectively. 而
Mixed strategy: example ◼ Matching pennies ◼ Player 1 has two pure strategies: H and T ( 1 (H)=0.5, 1 (T)=0.5 ) is a Mixed strategy. That is, player 1 plays H and T with probabilities 0.5 and 0.5, respectively. ( 1 (H)=0.3, 1 (T)=0.7 ) is another Mixed strategy. That is, player 1 plays H and T with probabilities 0.3 and 0.7, respectively. 10

Mixed strategy:example Player 2 L(O) C(113) R(213) T(3/4) 0 2 3, 3 1, 1 Player 1 M(O) 4 0 0, ¥ 2, 3 B(1/4) 4 5, 1 01 7 Player 1: >(3/4,0,4)is a mixed strategy.That is, o1(T)=3/4,o1(M)=0ando1(B)=1/4. ■ Player 2: >(0,1/3,2/3)is a mixed strategy.That is, o2(L)=0,o2(C)=1/3ando2(R)=2/3. 1
Mixed strategy: example Player 2 L (0) C (1/3) R (2/3) Player 1 T (3/4) 0 , 2 3 , 3 1 , 1 M (0) 4 , 0 0 , 4 2 , 3 B (1/4) 3 , 4 5 , 1 0 , 7 11 ◼ Player 1: ➢ (3/4, 0, ¼) is a mixed strategy. That is, 1 (T)=3/4, 1 (M)=0 and 1 (B)=1/4. ◼ Player 2: ➢ (0, 1/3, 2/3) is a mixed strategy. That is, 2 (L)=0, 2 (C)=1/3 and 2 (R)=2/3