《构造地质学》课程教学资源（教材讲义）第四章 岩石变形的力学分析

第四章岩石变形的力学分析 地壳岩石中千姿百态的构造变形，地质构造的基本形态、组合类型、分布规律，都是地 壳运动产生的力导致岩石发生变形和位移的结果。岩石的力学性质及所处的地质环境决定着 地质构造的特征。因此，要正确理解岩石变形、地质构造及其形成过程，研究各种构造变形 的力学成因和相关规律，必须了解力学的一些基本概念和原理，根据作用在岩石上产生应力 的外力系统和由这些应力所引起的应变或变形的几何形态变化来对变形进行理论分析，从而 为构造研究提供理论依据，解决石油、天然气等资源勘探与开发中的构造问题。 本章要点：本章在介绍应力和应变分析后，重点阐述了岩石变形习性的基本规律和特点， 最后进行了影响岩石力学性质和变形各种因素的讨论。要求学生了解构造应力的概念及简单 构造的应力分析方法，掌握应力分析的基本知识和岩石变形的规律特征，掌握影响岩石力学 性质和变形的各种因素。 第一节应力与应变 一、应力分析 (一)力的基木将今 1.作用力 力：力是物体间的相互作用，并且是一个矢量，它不仅有大小，而且有方向。 力的合成与分解：任何一个作用力都可以按平行四边形法则分解成的两个分力来表示 而任何两个分力也可以用一个合力来表示。如图41A表示力F怎样分解成呈直角的两分量 F1和F:反之，图41B表示任何两个力F:和F2怎样由其合力F来代表。 图4一1力的分解与合成 逆时针剪切力 顺时针剪切力 图4一2物体受力示意图

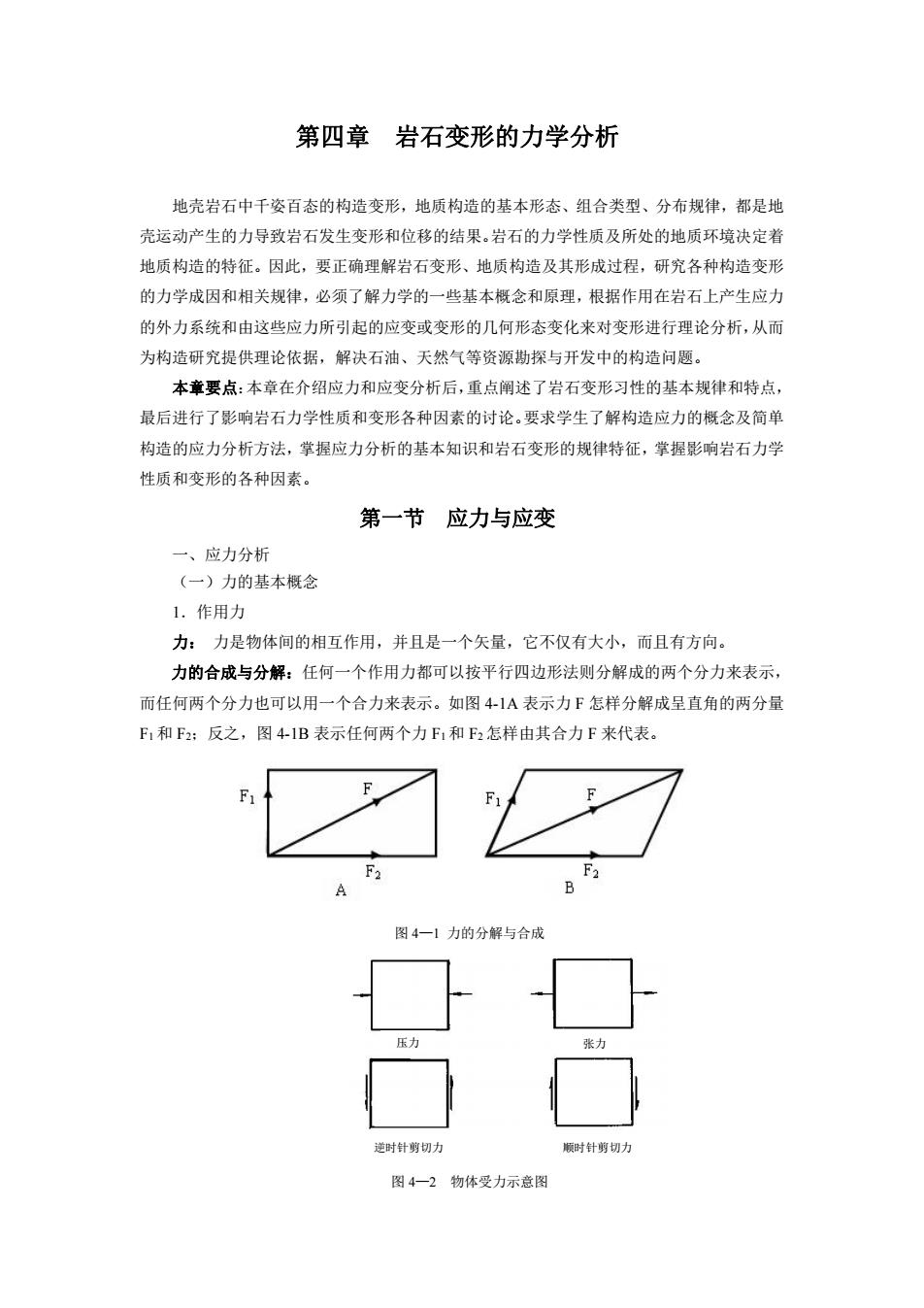
第四章 岩石变形的力学分析 地壳岩石中千姿百态的构造变形，地质构造的基本形态、组合类型、分布规律，都是地 壳运动产生的力导致岩石发生变形和位移的结果。岩石的力学性质及所处的地质环境决定着 地质构造的特征。因此，要正确理解岩石变形、地质构造及其形成过程，研究各种构造变形 的力学成因和相关规律，必须了解力学的一些基本概念和原理，根据作用在岩石上产生应力 的外力系统和由这些应力所引起的应变或变形的几何形态变化来对变形进行理论分析，从而 为构造研究提供理论依据，解决石油、天然气等资源勘探与开发中的构造问题。 本章要点：本章在介绍应力和应变分析后，重点阐述了岩石变形习性的基本规律和特点， 最后进行了影响岩石力学性质和变形各种因素的讨论。要求学生了解构造应力的概念及简单 构造的应力分析方法，掌握应力分析的基本知识和岩石变形的规律特征，掌握影响岩石力学 性质和变形的各种因素。 第一节 应力与应变 一、应力分析 （一）力的基本概念 1．作用力 力： 力是物体间的相互作用，并且是一个矢量，它不仅有大小，而且有方向。 力的合成与分解：任何一个作用力都可以按平行四边形法则分解成的两个分力来表示， 而任何两个分力也可以用一个合力来表示。如图 4-1A 表示力 F 怎样分解成呈直角的两分量 F1和 F2；反之，图 4-1B 表示任何两个力 F1和 F2怎样由其合力 F 来代表。 图 4—1 力的分解与合成 压力 张力 逆时针剪切力 顺时针剪切力 图 4—2 物体受力示意图

作用在物体上的力，往往都是成对出现的（作用力和反作用力大小相等方向相反）。有 两种方式，如图4-2所示： 张力和压力两个力作用在一条直线上，大小相等，方向相反，使受力物体沿作用力的 方向拉伸或缩短，我们分别称之为张力或压力，并规定压力为正，张力为负。 剪切力或扭力两个大小相等、方向相反的力，没有作用在一条直线上，使受力物体具 有旋转趋势，我们称之为剪切力或扭力，并规定逆时针剪切力为正，顺时针剪切力为负。 2.外力 外力是指一个物体作用在另一个物体上的力，可分为面力和体力 面力指互相接触的两个物体之间通过接触面传导的作用力， 体力指作用在两个物体之间，通过物体内部的各个质点同时受到影响的作用力，如重 力或物体之间的引力，它们与物体的质量成正比。 3.内力 内力是指同一物体内部各质点之间相互作用的力。 一个物体在没有受到外力作用的情况下，物体内部的各个质点之间具有一定的作用力， 大小相等，方向相反，使物体保持稳定平衡状态。物体内部各个质点之间的这种作用力称为 固有内力。 如果物体上受到外力的作用，那么物体内部各质点间的相互作用力将会随之发生变化。 这种物体内部质点间作用力的改变量称为附加内力。附加内力是物体内部质点对于所施加外 力的反映，它将力图使物体内部质点恢复其固有的位置，阻止物体发生变形。外力加大，附 加内力也随之增加，受力物体可能保持原来的平衡状态，但是所有的受力物体按其特有的质 地、形状、大小，都会有一个承受极限，一旦外力增加到超过这个极限时，受力物体就要发 生变形以至破坏。 由此可见，固有内力是每种物质所特有的，是这种物质保持其形状的质点间的作用力。 附加内力则反映了外力作用的一种效果，是导致物体发生变形和破坏的质点间的作用力。 图4-3外力和内力 我们者重讨论物体受力后的变形和破坏问题，为使问题简化，假定固有内力等于零，而 将附加内力简称为内力，并与外力对应。如图4-3所示，当外力P作用于物体时，物体内部 便产生与外力作用相抗衡的内力P,假定将这个物体沿A面切开，取出其中一部分而保留它

作用在物体上的力，往往都是成对出现的（作用力和反作用力大小相等方向相反）。有 两种方式，如图 4-2 所示： 张力和压力 两个力作用在一条直线上，大小相等，方向相反，使受力物体沿作用力的 方向拉伸或缩短，我们分别称之为张力或压力，并规定压力为正，张力为负。 剪切力或扭力 两个大小相等、方向相反的力，没有作用在一条直线上，使受力物体具 有旋转趋势，我们称之为剪切力或扭力，并规定逆时针剪切力为正，顺时针剪切力为负。 2．外力 外力是指一个物体作用在另一个物体上的力，可分为面力和体力。 面力 指互相接触的两个物体之间通过接触面传导的作用力， 体力 指作用在两个物体之间，通过物体内部的各个质点同时受到影响的作用力，如重 力或物体之间的引力，它们与物体的质量成正比。 3．内力 内力是指同一物体内部各质点之间相互作用的力。 一个物体在没有受到外力作用的情况下，物体内部的各个质点之间具有一定的作用力， 大小相等，方向相反，使物体保持稳定平衡状态。物体内部各个质点之间的这种作用力称为 固有内力。 如果物体上受到外力的作用，那么物体内部各质点间的相互作用力将会随之发生变化。 这种物体内部质点间作用力的改变量称为附加内力。附加内力是物体内部质点对于所施加外 力的反映，它将力图使物体内部质点恢复其固有的位置，阻止物体发生变形。外力加大，附 加内力也随之增加，受力物体可能保持原来的平衡状态，但是所有的受力物体按其特有的质 地、形状、大小，都会有一个承受极限，一旦外力增加到超过这个极限时，受力物体就要发 生变形以至破坏。 由此可见，固有内力是每种物质所特有的，是这种物质保持其形状的质点间的作用力。 附加内力则反映了外力作用的一种效果，是导致物体发生变形和破坏的质点间的作用力。 图 4—3 外力和内力 我们着重讨论物体受力后的变形和破坏问题，为使问题简化，假定固有内力等于零，而 将附加内力简称为内力，并与外力对应。如图 4-3 所示，当外力 P 作用于物体时，物体内部 便产生与外力作用相抗衡的内力 P，假定将这个物体沿 A 面切开，取出其中一部分而保留它

对截面A的内力不变，这时截面A上的内力P与外力P大小相等，方向相反 4.应力 应力是作用在单位面积上的内力，是外力作用下物体内部产生的内力强度。应力的国际 单位为帕斯卡(Pascal),简称帕(Pa),即Nm2。同样，应力也是一个矢量，其方向与内 力的方向一致。 若内力在截面上的分布是均匀的，如图43，则作用在截面A上的应力为： S=P (公式41) 若内力在截面上的分布是不均匀的，则可用微积分方法，求得每一点的应力值。即： s-m架银 (公式42) 应力可根据平行四边形法则进行分解和合成。据应力的性质、方向及作用面的关系，可 分为合应力、正应力、剪应力等。 图4一4应力的分解 合应力是指物体内任意截面上与外力作用方向平行的应力，如图44中的S。运用平行 四边形法则可将合应力一分为二，一是与作用面垂直的应力，称正应力或直应力，如图34 中的：一是与作用面平行的应力，称剪应力或扭应力，如图44中的。合应力、正应力、 剪应力三者之间的关系可用下式表示： S=0+t (公式43) T,=S.sina (公式44) O.=S.cosa (公式45) 若外力作用方向与作用面垂直，则该作用面上只产生正应力，不产生剪应力，此时，我 们称该作用面为主平面，主平面上的正应力为主应力。 当正应力的方向向着作用面时，该正应力称为压应力：当正应力的方向是离开作用面时， 该正应力称为张应力。在构造地质学中规定：压应力为正，张应力为负：逆时针的剪应力为 正，顺时针的剪应力为负（如图4-5）

对截面 A 的内力不变，这时截面 A 上的内力 P 与外力 P 大小相等，方向相反。 4．应力 应力是作用在单位面积上的内力，是外力作用下物体内部产生的内力强度。应力的国际 单位为帕斯卡（Pascal）,简称帕（Pa），即 N/m2。同样，应力也是一个矢量，其方向与内 力的方向一致。 若内力在截面上的分布是均匀的，如图 4-3，则作用在截面 A 上的应力为：   S  （公式 4-1） 若内力在截面上的分布是不均匀的，则可用微积分方法，求得每一点的应力值。即：         d d S lim A 0 （公式 4-2） 应力可根据平行四边形法则进行分解和合成。据应力的性质、方向及作用面的关系，可 分为合应力、正应力、剪应力等。 图 4—4 应力的分解 合应力是指物体内任意截面上与外力作用方向平行的应力，如图 4-4 中的 S。运用平行 四边形法则可将合应力一分为二，一是与作用面垂直的应力，称正应力或直应力，如图 3-4 中的σ；一是与作用面平行的应力，称剪应力或扭应力，如图 4-4 中的τ。合应力、正应力、 剪应力三者之间的关系可用下式表示：   2 2 2 s   （公式 4-3）  S sin a   （公式 4-4）  S cos a   （公式 4-5） 若外力作用方向与作用面垂直，则该作用面上只产生正应力，不产生剪应力，此时，我 们称该作用面为主平面，主平面上的正应力为主应力。 当正应力的方向向着作用面时，该正应力称为压应力；当正应力的方向是离开作用面时， 该正应力称为张应力。在构造地质学中规定：压应力为正，张应力为负；逆时针的剪应力为 正，顺时针的剪应力为负（如图 4-5）

图4一5正、负剪应力示意图 一正剪应力：负应力 (二)应力状态 物体受力后，内部各个截面上将产生有规律分布的应力，我们称物体所处的这种力学状 态为应力状态。为了分析物体受力后各点各方向的应力情况，我们先研究一点的应力状态。 受力物体中某点的应力状态即为三维空间中该点应力的方向与大小。对于任一给定应力 状态，总有三个方向的面，它们彼此互相垂直且面上只有正应力作用（主应力），而剪应力 值为零。这样的三个面称为主应力面（主平面），三个主应力面分别受到来自其法线方向上 的主应力的作用。习惯上用1,2，表示最大主应力、中间主应力和最小主应力(> 2>)。这样，为简便表示点的应力状态，就可以考虑在该点取一无限小的立方体，研究 作用在一个无限小的立方体上的力的效应。 根据主应力存在的情况，可以将应力状态分为三种基本类型 单应力状态两个主应力为零的应力状态，只有存在 G10,02=0=0 两向应力状态一个主应力为零的应力状态，存在，和2，又称平面应力状态： 010:020:0=0 三向应力状态三个主应力均不为零的应力状态，存在G1、2和，又称空间应力状态 G10:00:60:且o1>>G 在实际问题研究中，空间应力状态往往可以简化为平面应力状态，而单应力状态可视为 平面应力状态的特例。所以我们下面着重分析平面应力状态。 根据小立方体与应力的关系，平面应力状态又可分为平面主应力状态、平面纯剪应力状 态和平面一般应力状态」 1,平面主应力状态 平面主应力状态是指小立方体只受到两个垂直方向上主应力作用时的应力状态（图 4-6)。如图4-6，假定任意斜截面mn上的应力为S。,正应力为o,剪应力，mn外法线与 o1正向交角为a。o1、o2在mn面上的分量（正应力、剪应力）分别为：Gal、:tal、t@ 则有： S:=0:+T: (公式4-6)

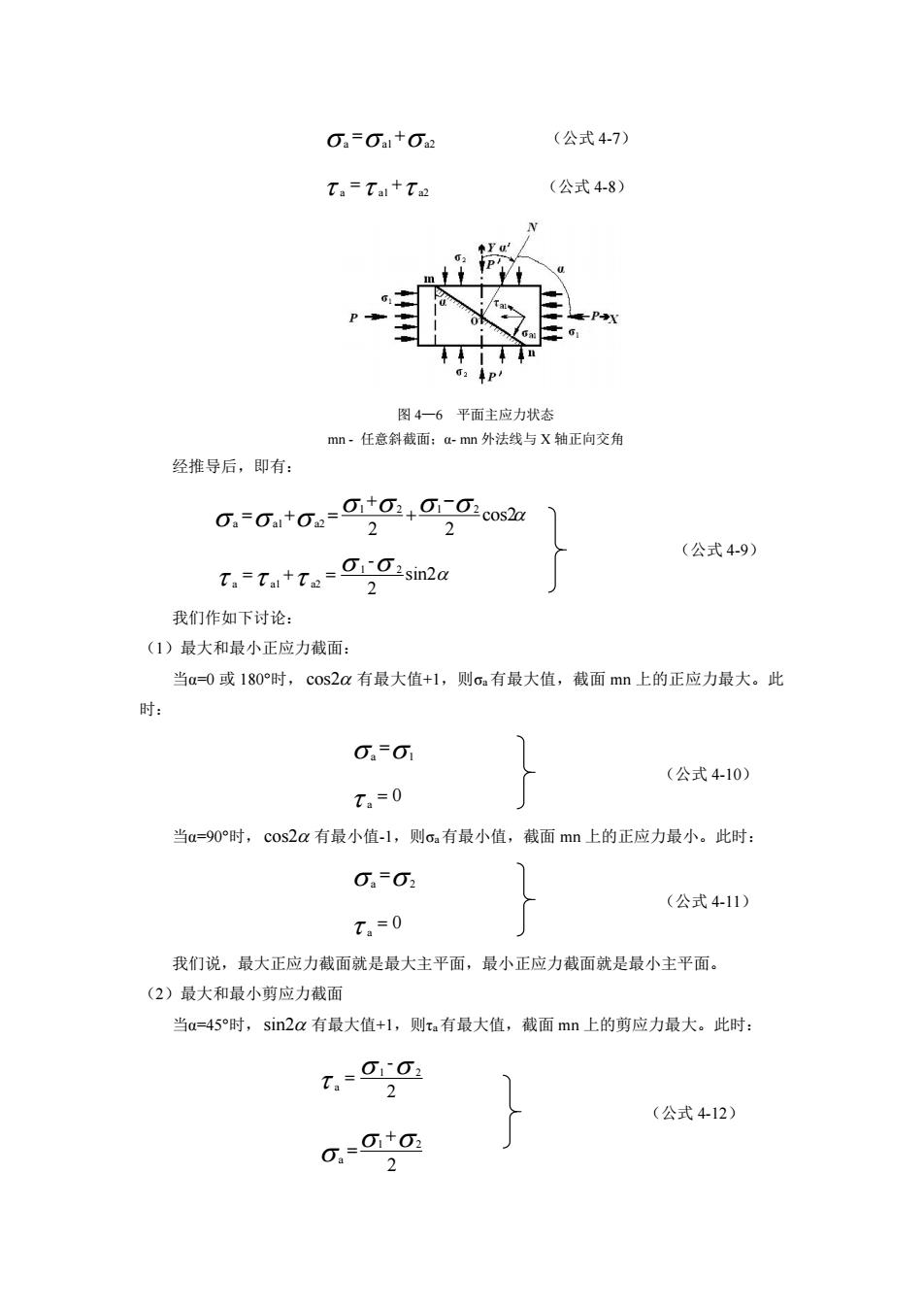
图 4—5 正、负剪应力示意图 τa–正剪应力；τb-负剪应力 （二）应力状态 物体受力后，内部各个截面上将产生有规律分布的应力，我们称物体所处的这种力学状 态为应力状态。为了分析物体受力后各点各方向的应力情况，我们先研究一点的应力状态。 受力物体中某点的应力状态即为三维空间中该点应力的方向与大小。对于任一给定应力 状态，总有三个方向的面，它们彼此互相垂直且面上只有正应力作用（主应力），而剪应力 值为零。这样的三个面称为主应力面（主平面），三个主应力面分别受到来自其法线方向上 的主应力的作用。习惯上用σ1，σ2，σ3，表示最大主应力、中间主应力和最小主应力（σ1＞ σ2＞σ3）。这样，为简便表示点的应力状态，就可以考虑在该点取一无限小的立方体，研究 作用在一个无限小的立方体上的力的效应。 根据主应力存在的情况，可以将应力状态分为三种基本类型 单应力状态 两个主应力为零的应力状态，只有σ1存在： σ1≠0，σ2=σ3= 0 两向应力状态 一个主应力为零的应力状态，存在σ1和σ2，又称平面应力状态： σ1≠0；σ2≠0；σ3= 0 三向应力状态 三个主应力均不为零的应力状态，存在σ1、σ2和σ3，又称空间应力状态： σ1≠0；σ2≠0；σ3≠ 0；且σ1＞σ2＞σ3 在实际问题研究中，空间应力状态往往可以简化为平面应力状态，而单应力状态可视为 平面应力状态的特例。所以我们下面着重分析平面应力状态。 根据小立方体与应力的关系，平面应力状态又可分为平面主应力状态、平面纯剪应力状 态和平面一般应力状态。 1．平面主应力状态 平面主应力状态是指小立方体只受到两个垂直方向上主应力作用时的应力状态（图 4-6）。如图 4-6，假定任意斜截面 mn 上的应力为 Sa，正应力为σa，剪应力τa，mn 外法线与 σ1正向交角为α。σ1、σ2在 mn 面上的分量（正应力、剪应力）分别为：σa1、σa2 ；τa1、τa2。 则有：   2 a 2 a 2 Sa   （公式 4-6）

0=0a1+0 (公式4-7) Ta=Tal+Ta (公式4-8) 图4一6平面主应力状态 mn任意斜截面：am外法线与X轴正向交角 经推导后，即有： 2 t。=ta+tn-o:asin2a (公式49) 2 我们作如下讨论： (1)最大和最小正应力截面： 当a=0或180时，cos2a有最大值+1，则c,有最大值，截面mn上的正应力最大。此 时： 00 (公式410) t,=0 当a=90时，cos2a有最小值-l,则o有最小值，截面mn上的正应力最小。此时： 0。=02 (公式411) t。=0 我们说，最大正应力截面就是最大主平面，最小正应力截面就是最小主平面。 (2)最大和最小剪应力截面 当a=45时，sin2a有最大值+1，则有最大值，截面mn上的剪应力最大。此时： 1,-00, (公式412) 0.-aita 2

（公式 4-12） a a1 a2   （公式 4-7）  a  a1  a2   （公式 4-8） 图 4—6 平面主应力状态 mn - 任意斜截面；α- mn 外法线与 X 轴正向交角 经推导后，即有： （公式 4-9）        cos2 2 2 1 2 1 2 a a1 a2            sin2 2 - 1 2 a a1 a2    我们作如下讨论： （1）最大和最小正应力截面： 当α=0 或 180°时， cos2 有最大值+1，则σa 有最大值，截面 mn 上的正应力最大。此 时： a 1  0 a   当α=90°时，cos2 有最小值-1，则σa有最小值，截面 mn 上的正应力最小。此时： a 2  0 a   我们说，最大正应力截面就是最大主平面，最小正应力截面就是最小主平面。 （2）最大和最小剪应力截面 当α=45°时，sin2 有最大值+1，则τa有最大值，截面 mn 上的剪应力最大。此时： 2 - 1 2 a     2 1 2 a      （公式 4-10） （公式 4-11）