
当a=135时,sin2a有最小值-1,而a仍有最大值(负号仅说明x,的方向为顺时针)。 此时: t.-00; 2 (公式413) a.-ata 当a=0°、90°、180°时,sin2a=0,则x值为0(见公式4-10和公式4-11)。 我们说,最大剪应力截面分别是a=45时的斜截面mn和a=135时的斜截面mn,其上 所受到的剪应力大小相等、方向相反,均有大小为严的正应力,且二面角为90°。剪应力 ,值为0的截面是a-0°、90°、180时的截面,该截面上没有剪应力,但却有最大和最小正 应力(见公式410和公式411). 2.平面纯剪应力状态 平面纯剪应力状态是指小立方体受力的四个面只作用者剪应力,而无正应力时的应力状 态(图4-7a)。 图4一7平面纯剪应力状态 经推导,平面纯剪应力状态下,任意截面上的应力为: .=t.sin2a (公式4-14) T.=-t.con2a (公式415) 我们作最大和最小正应力截面的讨论: 当a-45时,G=,为最大,同时a0。此时的截面,即为最大主应力61作用的主平面 (图4-7c). 当=135时,0=-t,为最大(负号说明是张应力),同时-0。此时的截面,即为最 小主应力o2作用的主平面(图47C)。 由此,σ1与σ2大小(等于纯剪应力π的绝对值)相等,符号相反。若将小立方体顺时针 或逆时针旋转45°,则该小立方体所处的应力状态由平面纯剪应力状态变为平面主应力状态 (图4-7c)
(公式 4-13) 当α=135°时,sin2 有最小值-1,而τa 仍有最大值(负号仅说明τa 的方向为顺时针)。 此时: 2 - 1 2 a 2 1 2 a 当α=0°、90°、180°时,sin2 =0,则τa值为 0(见公式 4-10 和公式 4-11)。 我们说,最大剪应力截面分别是α =45°时的斜截面 mn 和α=135°时的斜截面 m′n′,其上 所受到的剪应力大小相等、方向相反,均有大小为 2 1 2 的正应力,且二面角为 90°。剪应力 τa 值为 0 的截面是α=0°、90°、180°时的截面,该截面上没有剪应力,但却有最大和最小正 应力(见公式 4-10 和公式 4-11)。 2.平面纯剪应力状态 平面纯剪应力状态是指小立方体受力的四个面只作用着剪应力,而无正应力时的应力状 态(图 4-7a)。 图 4—7 平面纯剪应力状态 经推导,平面纯剪应力状态下,任意截面上的应力为: sin2 a (公式 4-14) con2 a (公式 4-15) 我们作最大和最小正应力截面的讨论: 当α=45°时,σa = τ,为最大,同时τa =0。此时的截面,即为最大主应力σ1作用的主平面 (图 4-7c)。 当α=135°时,σa = -τ,为最大(负号说明是张应力),同时τa =0。此时的截面,即为最 小主应力σ2作用的主平面(图 4-7c)。 由此,σ1与σ2 大小(等于纯剪应力τ的绝对值)相等,符号相反。若将小立方体顺时针 或逆时针旋转 45°,则该小立方体所处的应力状态由平面纯剪应力状态变为平面主应力状态 (图 4-7c)
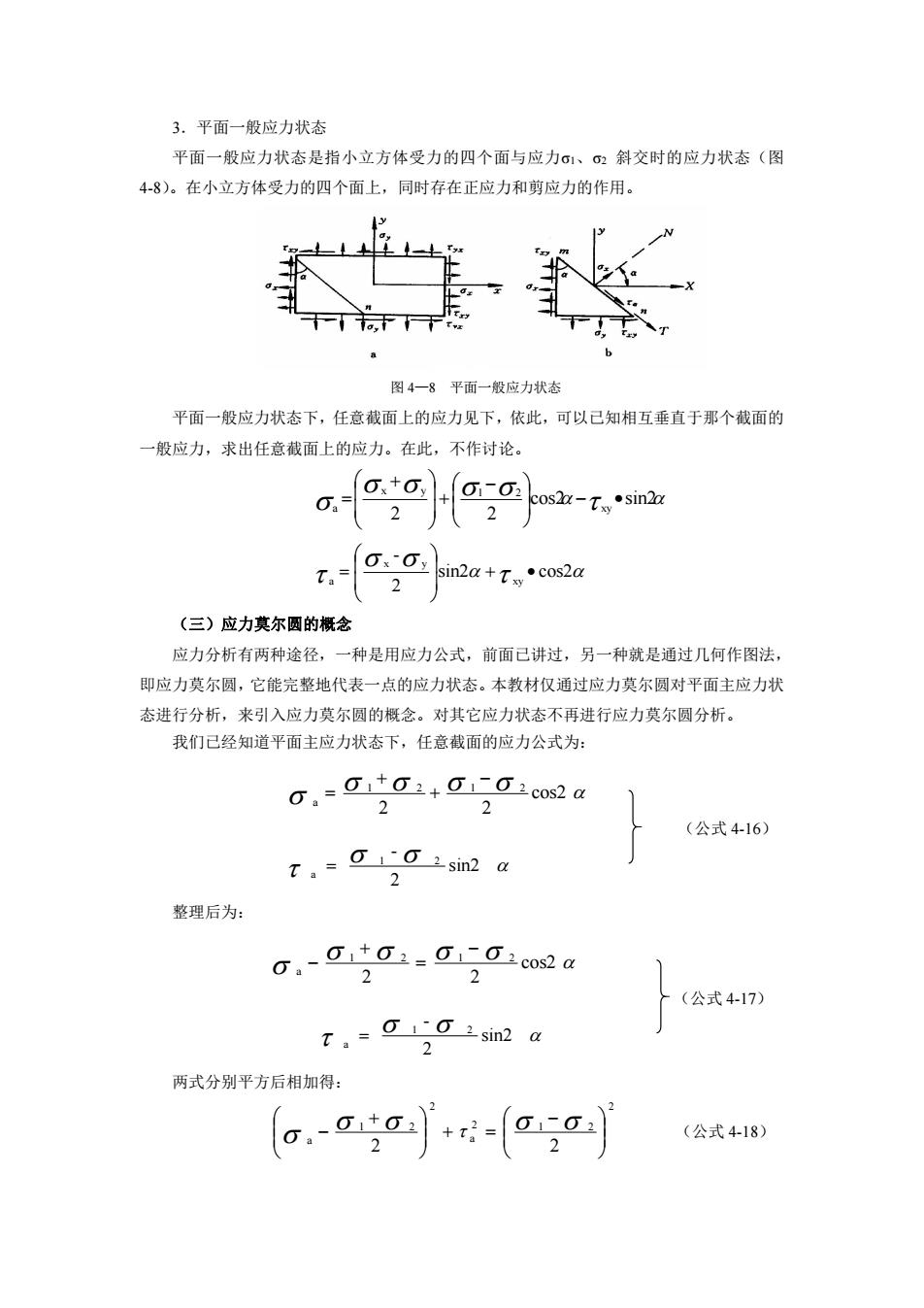
3.平面一般应力状态 平面一般应力状态是指小立方体受力的四个面与应力σ、2斜交时的应力状态(图 48)。在小立方体受力的四个面上,同时存在正应力和剪应力的作用。 图4一8平面一般应力状态 平面一般应力状态下,任意截面上的应力见下,依此,可以已知相互垂直于那个截面的 般应力,求出任意截面上的应力。在此,不作讨论。 a-00 t,= 2 (三)应力莫尔圆的概念 应力分析有两种途径,一种是用应力公式,前面已讲过,另一种就是通过几何作图法, 即应力莫尔圆,它能完整地代表一点的应力状态。本教材仅通过应力莫尔圆对平面主应力状 态进行分析,来引入应力莫尔圆的概念。对其它应力状态不再进行应力莫尔圆分析。 我们已经知道平面主应力状态下,任意截面的应力公式为: 0.=g101+0702cos2g 2 2 (公式416) T,-Gsin2 a 2 整理后为: 0.-01101-004co2a 2 2 (公式4-17) 两式分别平方后相加得 G.-ota: 2 +=oo2 (公式4-18) 2
(公式 4-16) (公式 4-17) 3.平面一般应力状态 平面一般应力状态是指小立方体受力的四个面与应力σ1、σ2 斜交时的应力状态(图 4-8)。在小立方体受力的四个面上,同时存在正应力和剪应力的作用。 图 4—8 平面一般应力状态 平面一般应力状态下,任意截面上的应力见下,依此,可以已知相互垂直于那个截面的 一般应力,求出任意截面上的应力。在此,不作讨论。 cos2 sin2 2 2 xy x y 1 2 a sin2 cos2 2 - xy x y a (三)应力莫尔圆的概念 应力分析有两种途径,一种是用应力公式,前面已讲过,另一种就是通过几何作图法, 即应力莫尔圆,它能完整地代表一点的应力状态。本教材仅通过应力莫尔圆对平面主应力状 态进行分析,来引入应力莫尔圆的概念。对其它应力状态不再进行应力莫尔圆分析。 我们已经知道平面主应力状态下,任意截面的应力公式为: cos2 2 2 1 2 1 2 a sin2 2 - 1 2 a 整理后为: cos2 2 2 1 2 1 2 a sin2 2 - 1 2 a 两式分别平方后相加得: 2 2 1 2 a 2 1 2 a 2 2 (公式 4-18)

在o为横坐标,为纵坐标的直角坐标系中,此式为圆的方程,其圆心为0,半 径为,。此圆为平面主应力莫尔圆(图49)。应力莫尔圆代表物体内一点的应力状态 经过这一点的任意截面上的应力分量σ和等于莫尔圆上对应的横坐标和纵坐标。 图4一9平面主应力莫尔圆 如图49所示,最大主平面b上的应力有莫尔圆上的A点所代表,A点的横坐标为o 是正应力的最大值,纵坐标为零,即最大主平面是最大正应力作用面,该平面上无剪应力。 最小主平面C上的应力由莫尔圆上的B点所代表,该点的横坐标为6,纵坐标为零,即最 小主平面上作用者最小正应力。截面m的法线N与最大主应力轴c1的夹角为a,则截面 mn上的应力分量o和r,等于莫尔圆上D点的坐标,D点与A点相隔2a圆心角。 (四)应力场与构造应力场 1,应力场的彬今 受力岩石中的每一点都存在一个与该点对应的瞬时应力状态,一系列瞬时的点应力状态 组成的空间称为应力场。如果应力场中各点的应力状态都相同称为均匀应力场:相反,应力 场中各点的应力状态不相同,从一点到另一点其应力状态存在着变化,则称为非均匀应力场: 2.构造应力场的概念 构造应力场是指地壳内部一定范围内某一瞬时的应力状态,表示那一解间各点的应力状 态及其变化情况。构造应力场中应力的分布和变化是连续而有规律的。研究构造应力场的目 的就在于揭示一定范围内应力分布的规律,构造应力场的性质、地壳运动的方式、方向及区 域构造发育的制约关系,推断可能在何处出现的某种构造等,为找矿勘探工作和地震等灾害 的预报预防工作提供指导。 依照研究的规模可分为局部构造应力场、区域构造应力场和全球构造应力场:从时间上 来看,构造应力场又可分为古构造应力场和现代构造应力场。古构造应力场只能通过对已经 存在于地壳中的构造及其组合特征的分析与推断来恢复和研究。现代构造应力场则可以通过 仪器来测定。 3.构造应力场的表示 在构造应力场的研究中,要突出定时、定向、定量这三个方面的问题,即确定构造应力 场存在的时期、确定构造应力场的空间方位、确定应力值。 正如我们用磁力线、电力线来表示磁场与电场一样。对于构造应力场的表示,我们引入
在σ为横坐标,τ为纵坐标的直角坐标系中,此式为圆的方程,其圆心为 ,0 2 1 2 ,半 径为 2 1 2 。此圆为平面主应力莫尔圆(图 4-9)。应力莫尔圆代表物体内一点的应力状态, 经过这一点的任意截面上的应力分量σa和τa等于莫尔圆上对应的横坐标和纵坐标。 图 4—9 平面主应力莫尔圆 如图 4-9 所示,最大主平面 ab 上的应力有莫尔圆上的 A 点所代表,A 点的横坐标为σ1 是正应力的最大值,纵坐标为零,即最大主平面是最大正应力作用面,该平面上无剪应力。 最小主平面 ac 上的应力由莫尔圆上的 B 点所代表,该点的横坐标为σ2,纵坐标为零,即最 小主平面上作用着最小正应力。截面 mn 的法线 Na 与最大主应力轴σ1 的夹角为α,则截面 mn 上的应力分量σa和τa 等于莫尔圆上 D 点的坐标,D 点与 A 点相隔 2α圆心角。 (四)应力场与构造应力场 1.应力场的概念 受力岩石中的每一点都存在一个与该点对应的瞬时应力状态,一系列瞬时的点应力状态 组成的空间称为应力场。如果应力场中各点的应力状态都相同称为均匀应力场;相反,应力 场中各点的应力状态不相同,从一点到另一点其应力状态存在着变化,则称为非均匀应力场。 2.构造应力场的概念 构造应力场是指地壳内部一定范围内某一瞬时的应力状态,表示那一瞬间各点的应力状 态及其变化情况。构造应力场中应力的分布和变化是连续而有规律的。研究构造应力场的目 的就在于揭示一定范围内应力分布的规律,构造应力场的性质、地壳运动的方式、方向及区 域构造发育的制约关系,推断可能在何处出现的某种构造等,为找矿勘探工作和地震等灾害 的预报预防工作提供指导。 依照研究的规模可分为局部构造应力场、区域构造应力场和全球构造应力场;从时间上 来看,构造应力场又可分为古构造应力场和现代构造应力场。古构造应力场只能通过对已经 存在于地壳中的构造及其组合特征的分析与推断来恢复和研究。现代构造应力场则可以通过 仪器来测定。 3.构造应力场的表示 在构造应力场的研究中,要突出定时、定向、定量这三个方面的问题,即确定构造应力 场存在的时期、确定构造应力场的空间方位、确定应力值。 正如我们用磁力线、电力线来表示磁场与电场一样。对于构造应力场的表示,我们引入

应力迹线和应力网格的概念。 应力迹线是指应力场中某种应力方向的变化线。常用的应力迹线有最大主应力迹线、最 小主应力迹线和最大剪应力迹线(图410)。 应力网格是指几组应力迹线分布的几何图象(图4-10)。 X× 图4一10纯剪应力场的应力网格 a-主压应力迹线(o)和主张应力迹线(o,):b最大剪应力迹线 二变形和应变 (一)变形 1.变形的概今 物体受到应力作用,其内部各质点间的相对位置发生改变,称之为变形。物体变形可以 是形状的改变(形变),也可以是体积的改变(体变),或者二者均有改变。变形有两种最基 本的变形方式:线变形和剪变形。 线变形指物体受力时,表现为单纯的拉伸或压缩的变形,又称正变形(图411)。受 力后的小六面体仅仅是边长发生改变,表现出被伸长或被缩短。 剪变形指物体受力时,表现为物体内部任意截面都有一个旋转角度的变形,又称角变 形(图411)。受力后小六面体的直角变为锐角或者钝角。 图4一11线变形和剪变形示意图 P外力:c变形前的纵向长度:L变形后的纵向长度: H变形前的横向宽度:H变形后的横向宽度:剪变形旋转的角度 2.变形的方式 岩石变形最基本的形式是线变形和剪变形。它们组成五种基本的变形方式(图412) 拉伸:在张应力作用下的线变形。 压缩:在压应力作用下的线变形。 剪切:在简单剪切作用下的剪变形,使岩石被剪切错动或形态发生变化。 弯曲:在沿岩石长轴方向的压应力作用下或在弯梁作用下产生的变形,致使岩石发生弯
应力迹线和应力网格的概念。 应力迹线是指应力场中某种应力方向的变化线。常用的应力迹线有最大主应力迹线、最 小主应力迹线和最大剪应力迹线(图 4-10)。 应力网格是指几组应力迹线分布的几何图象(图 4-10)。 图 4—10 纯剪应力场的应力网格 a-主压应力迹线(σ1)和主张应力迹线(σ3);b-最大剪应力迹线 二 变形和应变 (一)变形 1.变形的概念 物体受到应力作用,其内部各质点间的相对位置发生改变,称之为变形。物体变形可以 是形状的改变(形变),也可以是体积的改变(体变),或者二者均有改变。变形有两种最基 本的变形方式:线变形和剪变形。 线变形 指物体受力时,表现为单纯的拉伸或压缩的变形,又称正变形(图 4-11)。受 力后的小六面体仅仅是边长发生改变,表现出被伸长或被缩短。 剪变形 指物体受力时,表现为物体内部任意截面都有一个旋转角度的变形,又称角变 形(图 4-11)。受力后小六面体的直角变为锐角或者钝角。 图 4—11 线变形和剪变形示意图 P-外力;L0-变形前的纵向长度;L-变形后的纵向长度; H0-变形前的横向宽度;H-变形后的横向宽度;γ-剪变形旋转的角度 2.变形的方式 岩石变形最基本的形式是线变形和剪变形。它们组成五种基本的变形方式(图 4-12): 拉伸:在张应力作用下的线变形。 压缩:在压应力作用下的线变形。 剪切:在简单剪切作用下的剪变形,使岩石被剪切错动或形态发生变化。 弯曲:在沿岩石长轴方向的压应力作用下或在弯梁作用下产生的变形,致使岩石发生弯

曲。在发生弯曲变形的岩石内部会有一个既不拉伸、也不压缩的中和面:在中和面内侧和外 侧,分别表现为压缩变形和拉伸变形。 扭转:在岩石的两端,与轴线垂直的平面上各作用一对大小相等、方向相反的力偶所产 生的变形 图4一2五种基本李形方式 拉伸:b-压缩:c剪切:d弯曲:c扭转 3.均匀变形和非均匀变形 均匀变形:岩石的各个部分的变形性质、方向和大小都相同的变形称为均匀变形。其特 征是变形前的直线和平面,变形后仍然是直线和平面,变形前互相平行的直线和平面,变形 后仍然互相平行。如拉伸、压缩和剪切属均匀变形。 非均匀变形:岩石的各个部分的变形性质、方向和大小都变化的变形称为非均匀变形。 如弯曲和扭转属非均匀变形。 均匀变形和非均匀变形是相对的概念,在一定的研究范围内,较大尺度下是非均匀变形 而在较小尺度下,则表现为均匀变形。如图3-13所示,就整体的弯曲变形而言,属于非均 匀变形,但各个局部可以近似地看作是均匀变形,而且任意两个相邻的小圆所反映的变形方 向、大小、性质的差别是不明显的。 图4一13弯曲变形整体为非均匀变形 局部可近似地看作是均匀变形 递进变形 岩石在受力条件不变的情况下,由初始形态变形为最终形态的过程,是由一系列连续发 生的解时无限小变形的累积过程,此过程称为递进变形。进而还可分为共轴递进变形和非共 轴递进变形,本书不作详细讲解
曲。在发生弯曲变形的岩石内部会有一个既不拉伸、也不压缩的中和面;在中和面内侧和外 侧,分别表现为压缩变形和拉伸变形。 扭转:在岩石的两端,与轴线垂直的平面上各作用一对大小相等、方向相反的力偶所产 生的变形。 图 4—12 五种基本变形方式 a-拉伸;b-压缩;c-剪切;d-弯曲;e-扭转 3.均匀变形和非均匀变形 均匀变形:岩石的各个部分的变形性质、方向和大小都相同的变形称为均匀变形。其特 征是变形前的直线和平面,变形后仍然是直线和平面,变形前互相平行的直线和平面,变形 后仍然互相平行。如拉伸、压缩和剪切属均匀变形。 非均匀变形:岩石的各个部分的变形性质、方向和大小都变化的变形称为非均匀变形。 如弯曲和扭转属非均匀变形。 均匀变形和非均匀变形是相对的概念,在一定的研究范围内,较大尺度下是非均匀变形, 而在较小尺度下,则表现为均匀变形。如图 3-13 所示,就整体的弯曲变形而言,属于非均 匀变形,但各个局部可以近似地看作是均匀变形,而且任意两个相邻的小圆所反映的变形方 向、大小、性质的差别是不明显的。 图 4—13 弯曲变形整体为非均匀变形, 局部可近似地看作是均匀变形 递进变形 岩石在受力条件不变的情况下,由初始形态变形为最终形态的过程,是由一系列连续发 生的瞬时无限小变形的累积过程,此过程称为递进变形。进而还可分为共轴递进变形和非共 轴递进变形,本书不作详细讲解