2.2.3电源两种模型之间的等效变换ARRRRIR电压源电流源由图a:U由图b: I = IRoU=E- IRoUEU = I,R- IRRoRoE =IsRo内阻相同。等效变换公式:EIs= R.112025/4/5
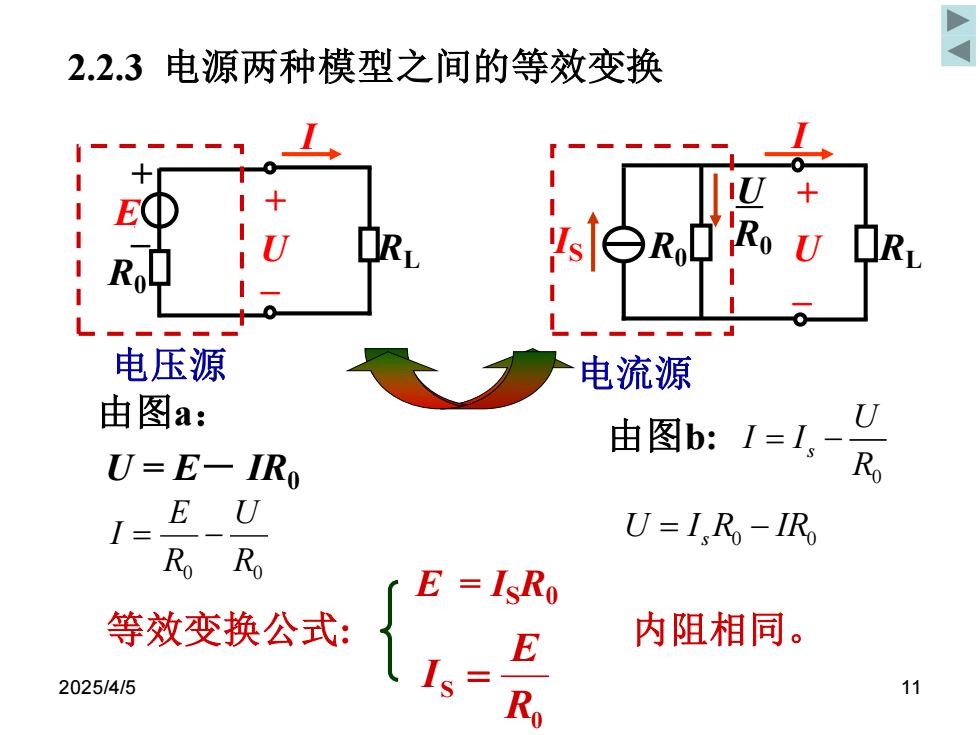
2025/4/5 11 2.2.3 电源两种模型之间的等效变换 由图a: U = E- IR0 I RL R0 + – E U + – 电压源 等效变换公式: E = ISR0 0 S R E I = R0 U RL R0 U IS I + – 电流源 0 R0 U R E I = − 由图b: 0 s U I I R = − U I R IR = − s 0 0 内阻相同
注意事项(1)电压源和电流源的等效关系只对外电路而言,对电源内部则是不等效的。(2)等效变换时,两电源的参考方向要一一对应。oaoaoa十oaEERoRoRoRobobobob(3)理想电压源与理想电流源之间无等效关系。(4)任何一个电动势E和某个电阻R串联的电路,都可化为一个电流为Is和这个电阻并联的电路122025/4/5
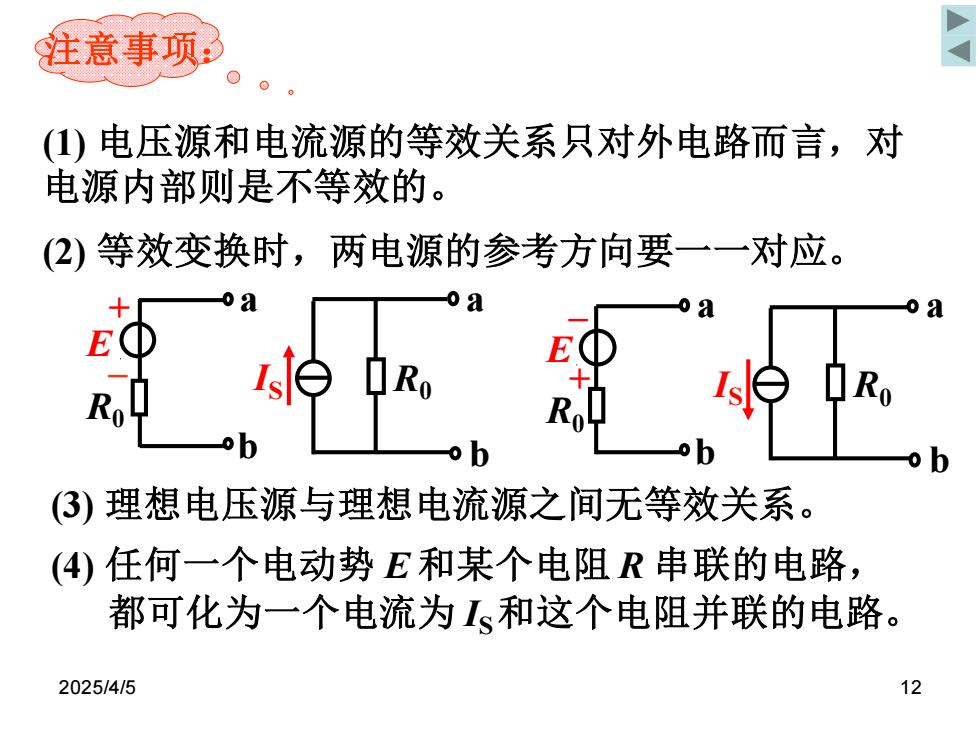
2025/4/5 12 (2) 等效变换时,两电源的参考方向要一一对应。 (3) 理想电压源与理想电流源之间无等效关系。 (1) 电压源和电流源的等效关系只对外电路而言,对 电源内部则是不等效的。 注意事项: (4) 任何一个电动势 E 和某个电阻 R 串联的电路, 都可化为一个电流为 IS 和这个电阻并联的电路。 R0 + – E a b IS R0 a b R0 – + E a b IS R0 a b

例1:求下列各电路的等效电源oaaa+222222UU5V(32U5A325vD2VCDOo bob(c)(a)(b)解:oaoaoa+++22UU5A032DsVU+Dsvobo bab(a)(b)(c)132025/4/5
2025/4/5 13 例1:求下列各电路的等效电源。 解: + – a b U 2 5V (a) + − + – a b 5V U (c) + − (c) a + - 2V + 5V U - b 2 + − (b) a U 5A 2 3 b + − (a) a + – 3 5V 2 U + − a 5A b 3 U (b) + −
A例2:试用电压源与电流源等效变换的方法计算2Q电阻中的电流D12Dno解2A12 12 2V-3262白20122262222A2A6VD①12V(b)1(a)由图(d)可得222V222V2222622228-2= 1A4A8V2+2+2(d)(c)142025/4/5
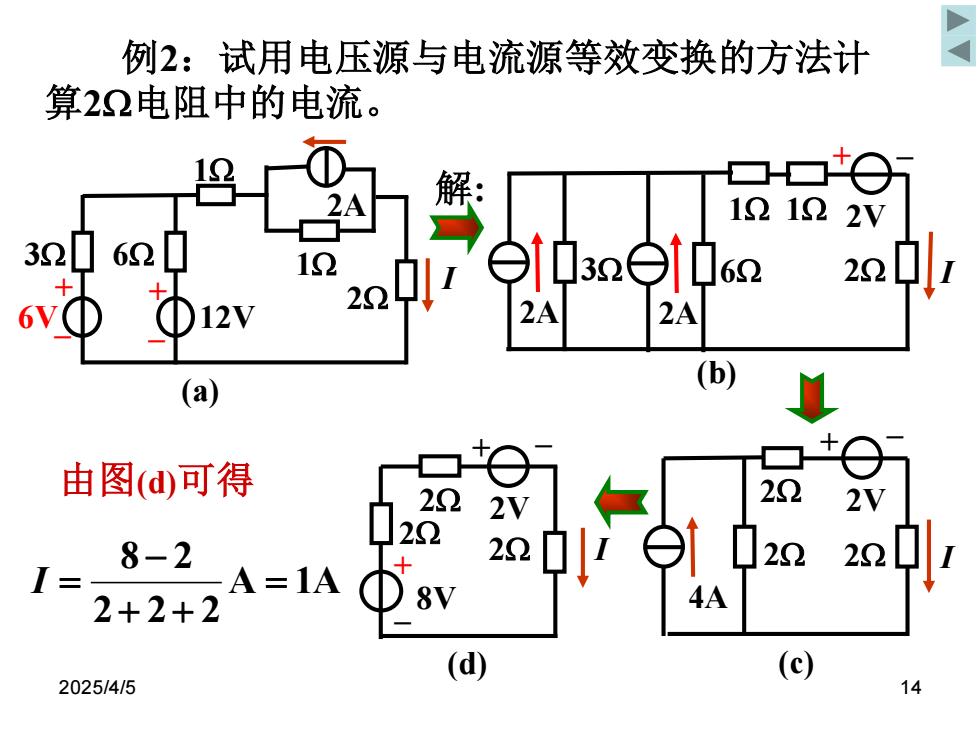
2025/4/5 14 例2:试用电压源与电流源等效变换的方法计 算2电阻中的电流。 A 1A 2 2 2 8 2 = + + − I = 解: – 8V + – 2 2V + 2 I (d) 2 由图(d)可得 6V 3 + – + – 12V 2A 6 1 1 2 I (a) 2A 3 1 2 2V + – I 2A 6 1 (b) 4A 2 2 2 2V + – I (c)
例3:试用电压源与电流源等效变换的方法计算图示电路中1Q电阻中的电流2 2口(6V?2A12324262解:统一电源形式2222广1222423262421e2A100~12二e?1A4A1A2A152025/4/5
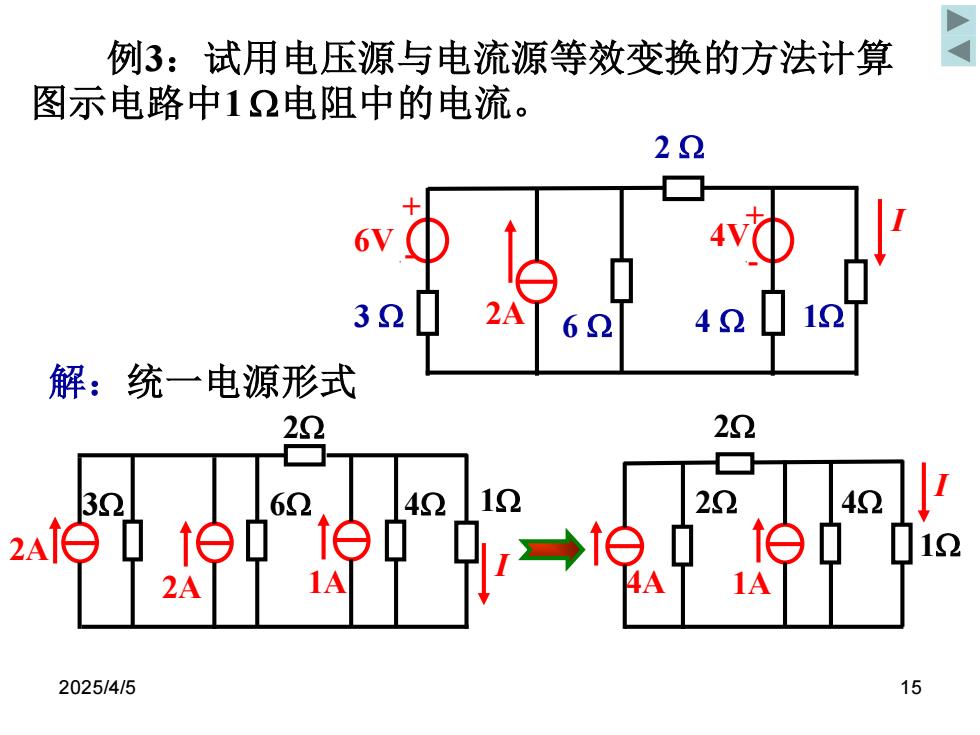
2025/4/5 15 解:统一电源形式 例3:试用电压源与电流源等效变换的方法计算 图示电路中1 电阻中的电流。 2 + - + - 6V 4V I 3 2A 6 4 1 2A 3 6 2A I 4 2 1 1A I 4 2 1 1A 2 4A