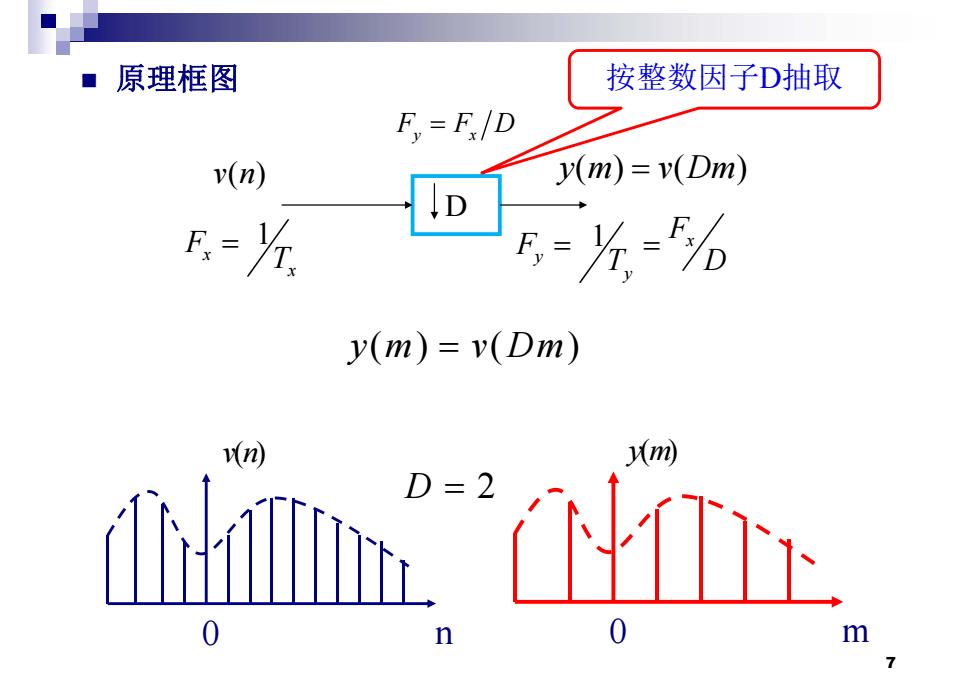
■ 原理框图 按整数因子D抽取 F,=F/D v(n) y(m)=v(Dm) D F=左 6=为% y(m)=v(Dm) n m D=2
原理框图 按整数因子D抽取 F FD y x 原理框图 按整数因子D抽取 D v n( ) y m v Dm () ( ) 1 1 F x x F T 1 x y y F F T D y m v Dm () ( ) v n( ) y( ) m D 2 7 0 n 0 m
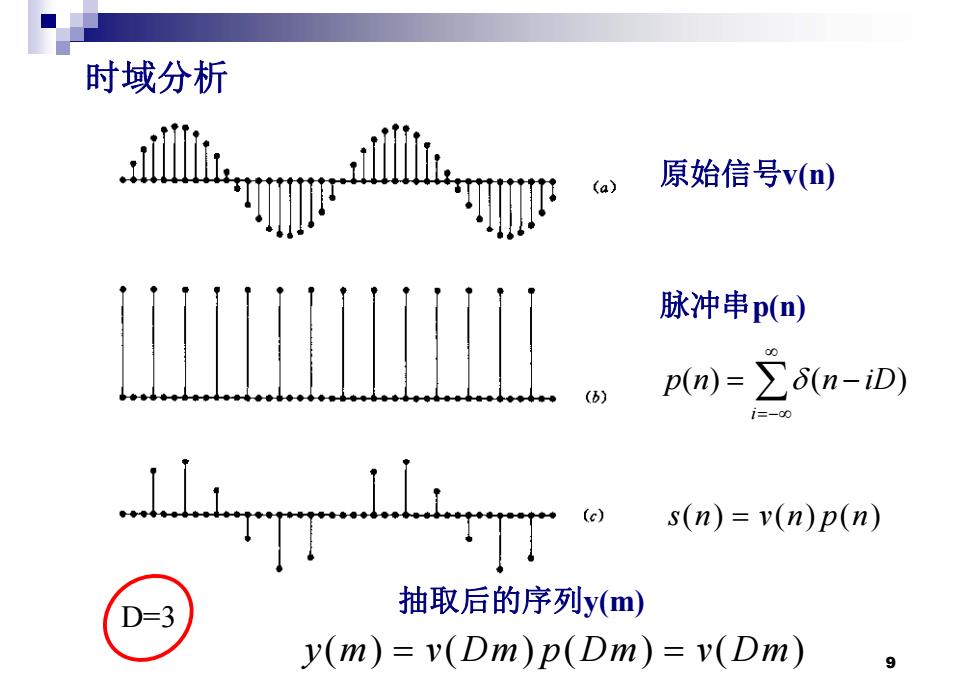
时域分析 (a) 原始信号v(n) 脉冲串p() p(n)=∑6n-iD) i=-00 TiiT s(n)=v(n)p(n) D=3 抽取后的序列y(m) y(m)=v(Dm)p(Dm)=v(Dm) 9
时域分析 原始信号v(n) 脉冲串p(n) p(n) (n iD) i p(n) (n iD) s() () () n vn pn D=3 抽取后的序列y(m) 9 D=3 y( ) y m v Dm p Dm v Dm () ( )( ) ( )

频谱关系 ■令s(n)=v(n)p(n) y(m)=s(Dm)=v(Dm)p(Dm) Y☑)=立mz“=∑sDma立s0W:n Y(Z)=>s(n)=v(p(m) DFS: =2 10
频谱关系 令 sn vn pn () () () y m s Dm v Dm p Dm () ( ) ( )( ) / ( ) ( ) ( ) () m m nD n Dm mm n Y Z y m z s Dm z s n z mm n / / ( ) () () () nD nD Y Z snz vn p n z ( ) () () () n n p 1 2 1 D j nk 0 1 : ( ) j nk D k DFS p n e D 1 2 1 / ( ) () D j nk D n D Y Z vn e z D 10 n k D 0

k=0n=-0 2)广62e v(n)台V(eo.) e)02re合e”=2rc 0,-2πk 0,=2T,0=2TxT=DT ∴0,=D0 Y(e D- D k=0 11
1 2 1 / ( ) () D j nk D n D Y Z 1 2 1 / ( ) D j nk D n D vne z / 0 ( ) () D n D n k Y Z vn e z D 0 ( ) D k n vne z D 2 2 1 1 0 1 / ( ) n j k D D k D z D vn e 1 2 0 1/ ( ) 1 j k D Dk D Ve z D D k0 n D k0 () ( ) x j vn V e 1 2 1/ 2 1 1 ( ) 1 () ( ) y y y D k j j D D j k D j Ve e D Ye Ve () ( ) 0 0 () ( ) ( ) k k Ve e D Ye Ve D y y x xy x T T T DT D ( ) 1 2 1 () ( ) y x k D D j j Y V y x D 0 11 () ( ) y D j k Y e V e D

2πk 0,=D0 2π @x-D →0,=2π 过整数因子D抽取,使数字须率区间0≤。,≤扩屉 成相应的频率区间0≤o,≤π 原采样信号频谱中o,>D 的非零频谱就会在0,=π 附近产生频谱混叠 12
2 k y x D ( ) 1 2 0 1 () ( ) y x k D D j j k Ye Ve D D k0 2 2 x y D 经过整数因子D抽取 使数字频率区间 0 扩展 经过整数因子D抽取,使数字频率区间 扩展 成相应的频率区间 0 x D 0 y 原采样信号频谱中 的非零频谱就会在 y x D y 附近产生频谱混叠 D 12