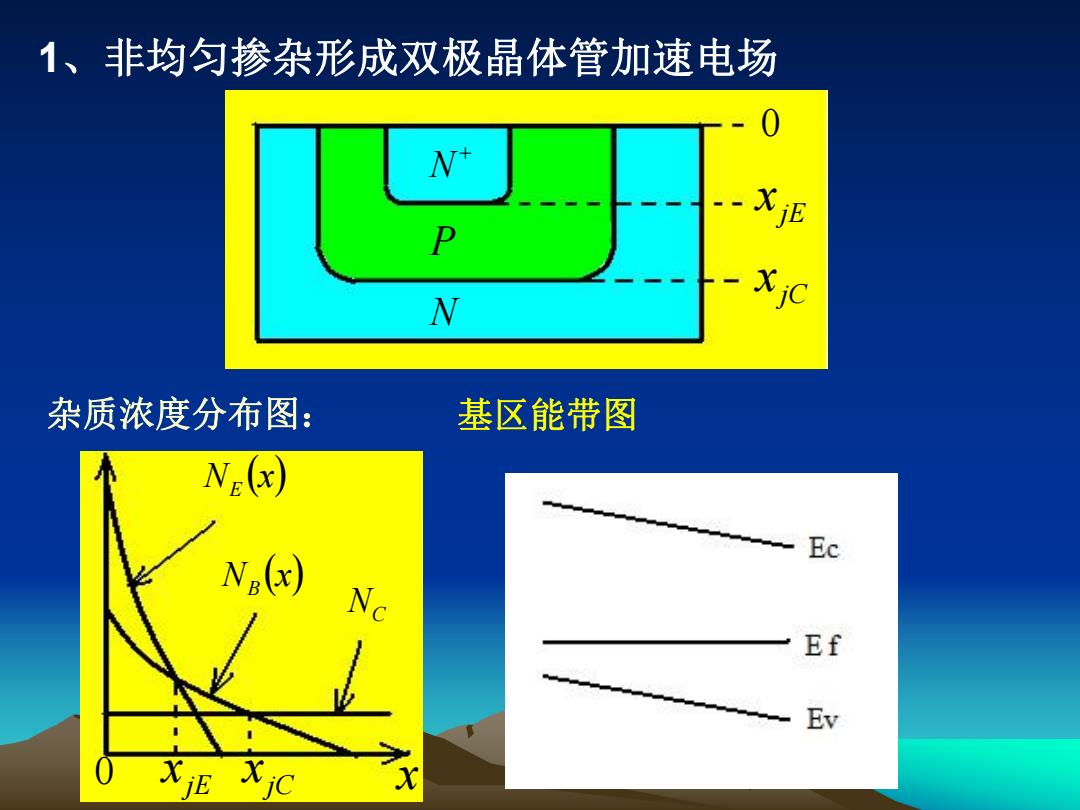
1、非均匀掺杂形成双极晶体管加速电场 N+ P N 杂质浓度分布图: 基区能带图 Nr(x) Ec (x) Ef Ev
1、非均匀掺杂形成双极晶体管加速电场 杂质浓度分布图: N x B 0 jC x 0 jE x xjE xjC x N x E NC P N N 基区能带图

设基区杂质浓度为: N.0 N() Ng(x)=Na(O)exp nx Ne(Wa) 式中刀是表征基区内杂质变化 程度的一个参数: NB(O) NeWa)=N0e”,7=lnNW。 当?=0时为均匀基区。 在实际的缓变基区晶体管中,7=48 小注入时,基区中总的多子浓度即为平衡多子浓度: PBx天pBO(6S=NBx
在实际的缓变基区晶体管中, 。 设基区杂质浓度为: 式中 是表征基区内杂质变化 程度的一个参数: 当 时为均匀基区。 小注入时,基区中总的多子浓度即为平衡多子浓度: 0 4 B B B W x N x N ( ) (0) exp p (x) p (x) N (x) B BO B ( ) (0) ( ) (0)e , ln B B B B B B N W N N W N 0 WB NB WB x 0 NB N x B 8

令基区多子电流为零: ,=g0+9,pg=0 dx 得内建电场为: E= De.1 dpa(x)D.1 dNp() H。PddH,Na )dx dN 由于 B<0E<0 ,故对电子起加速作用,称 为加速场
由于 , ,故对电子起加速作用,称 为加速场。 令基区多子电流为零: q p xE 0 dx dp x J qD p B B p p 得内建电场为: 0 E 0 dx dN B dx dN x N x D dx dp x p x D E B n B B n p B p 1 1
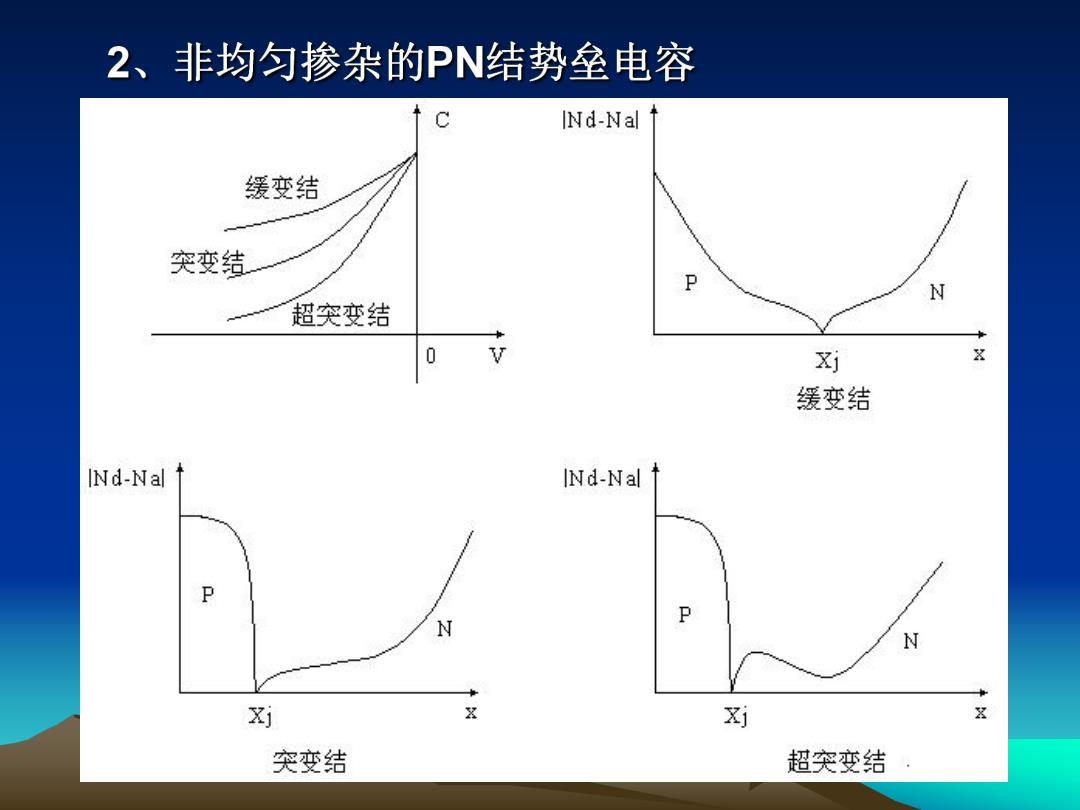
2、非均匀掺杂的PN结势垒电容 INd-Nal 缓变结 突变结 P N 超突变结 0 对 8 缓变结 INd-Nal INd-Nal P N P N X别 X对 X 突变结 超突变结
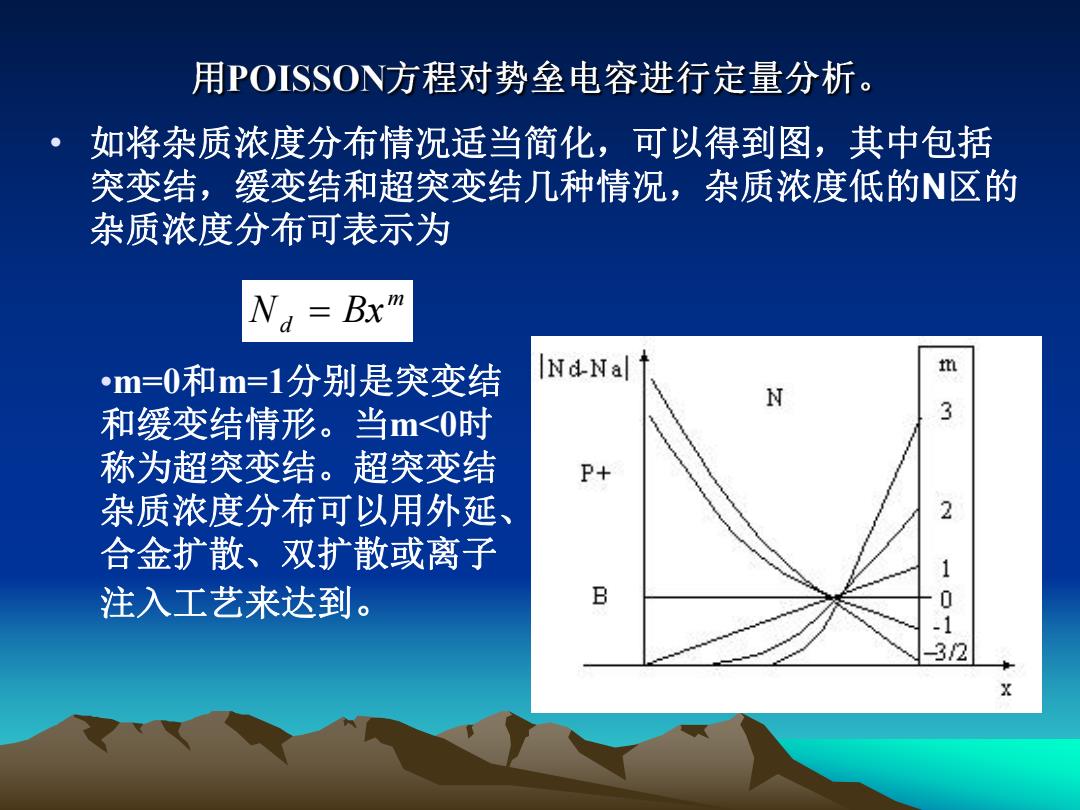
用POISSON方程对势垒电容进行定量分析。 如将杂质浓度分布情况适当简化,可以得到图,其中包括 突变结,缓变结和超突变结几种情况,杂质浓度低的N区的 杂质浓度分布可表示为 =Bxm m=0和m=1分别是突变结 Nd-Nal m N 和缓变结情形。当m<0时 3 称为超突变结。超突变结 P+ 杂质浓度分布可以用外延 2 合金扩散、双扩散或离子 注入工艺来达到。 B 101 32 X
• 如将杂质浓度分布情况适当简化,可以得到图,其中包括 突变结,缓变结和超突变结几种情况,杂质浓度低的N区的 杂质浓度分布可表示为 m Nd Bx •m=0和m=1分别是突变结 和缓变结情形。当m<0时 称为超突变结。超突变结 杂质浓度分布可以用外延、 合金扩散、双扩散或离子 注入工艺来达到