
Bloom Filters and its variants Original Author:Deke Guo Revised by Haipeng Dai Nanjing University 2015.11.27 Page 1
Page 1 Bloom Filters and its Variants Original Author: Deke Guo Revised by Haipeng Dai Nanjing University 201 5.11.27

Outline 1.Standard Bloom Filters 2.Compressed Bloom Filters 3.Counting Bloom Filters 4.Representation of a set of(key,f(key)) 5.Invertible Bloom Filters Page 2
Outline 1. Standard Bloom Filters 2. Compressed Bloom Filters 3. Counting Bloom Filters 4. Representation of a set of (key, f(key)) 5. Invertible Bloom Filters Page 2

The main point ▣ Whenever you have a set or list,and space is an issue,a Bloom filter may be a useful alternative. 3
3 The main point Whenever you have a set or list, and space is an issue, a Bloom filter may be a useful alternative

The Problem Solved by BF: Approximate Set Membership ☐ Given a set S={x.),construct data structure to answer queries of the form"Is y in S?" Data structure should be: Fast(Faster than searching through S). ■ Small(Smaller than explicit representation) To obtain speed and size improvements,allow some probability of error. ■ False positives:y gs but we reportyeS ■False negatives:y∈S but we reporty &S
4 The Problem Solved by BF: Approximate Set Membership Given a set S = { x 1,x 2,…,x n }, construct data structure to answer queries of the form “Is y in S?” Data structure should be: Fast (Faster than searching through S). Small (Smaller than explicit representation). To obtain speed and size improvements, allow some probability of error. False positives: y S but we report y S False negatives: y S but we report y S
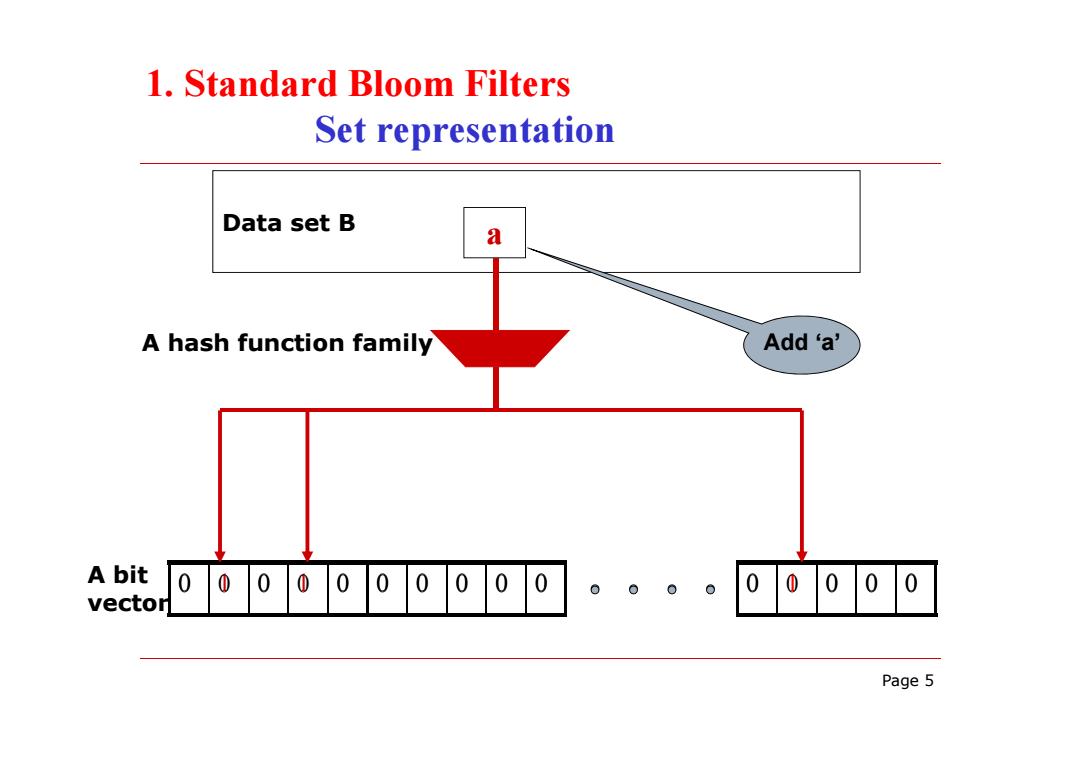
1.Standard Bloom Filters Set representation Data set B a A hash function family Add 'a' A bit 0000000000 0 00 00000 vector Page 5
Page 5 Data set B 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 a A hash function family A bit vector 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1. Standard Bloom Filters Set representation Add ‘a’