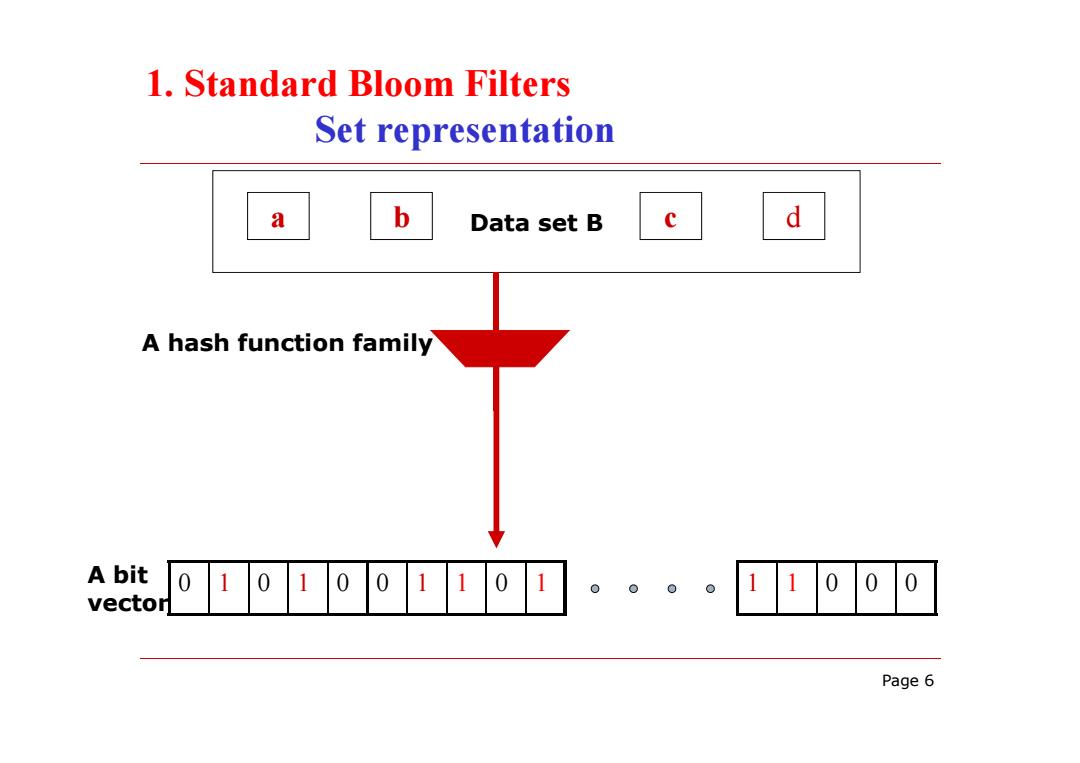
1.Standard Bloom Filters Set representation a b Data set B d A hash function family A bit vector Page 6
Page 6 0 1 0 1 0 0 1 1 0 1 1 1 0 0 0 a b Data set B c d A hash function family A bit vector 1. Standard Bloom Filters Set representation

1.Standard Bloom Filters Membership query ▣“Constant''time(time to hash) Small amount of space. But with some probability of being wrong. 7
7 “Constant” time (time to hash). Small amount of space. But with some probability of being wrong. 1. Standard Bloom Filters Membership query
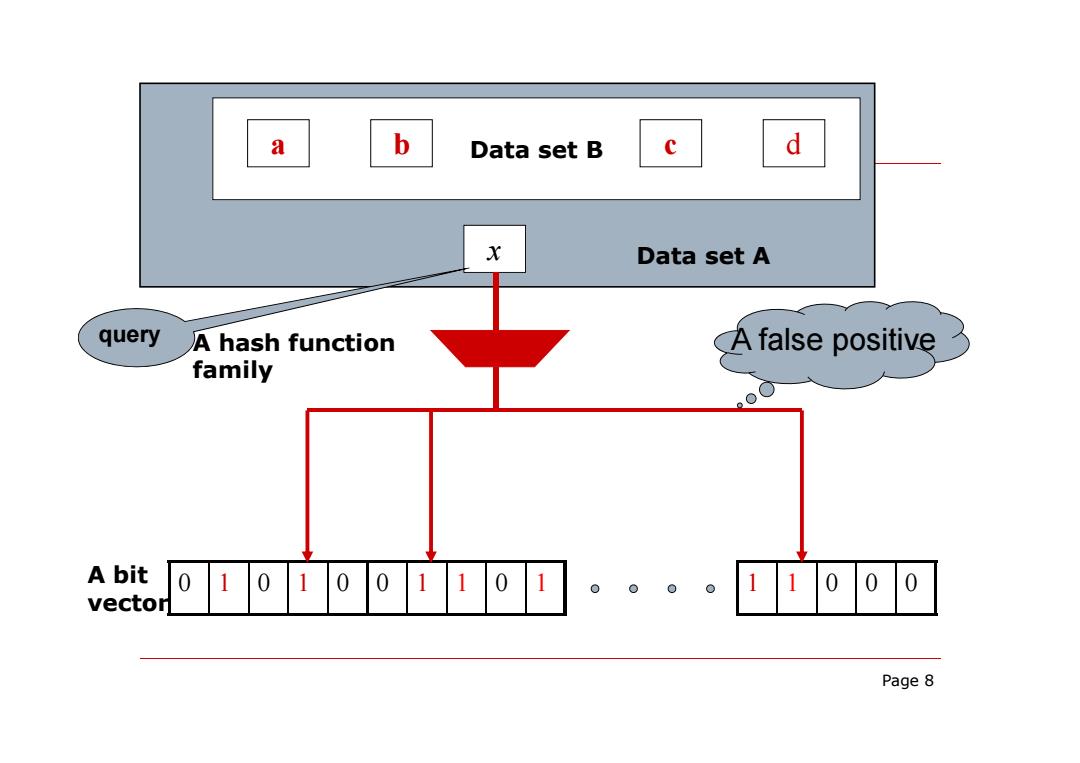
a b Data set B d Data set A query A hash function A false positive family A bit 01o1001101 vector 。。。。000 Page 8
Page 8 0 1 0 1 0 0 1 1 0 1 1 1 0 0 0 a b Data set B c d x Data set A A hash function family A bit vector query A false positive

False positive probability Assumption:We have good hash functions,look random. Given m bits for filter and n elements,choose number k of hash functions to minimize false positives: ■Let p=Pr[cell is empty ]=(1-1/m)kne-kn/m ■Let f=Pr[false pos]=(1-p)(1-e-kn/m As k increases,more chances to find a 0,but more 1's in the array. Find optimal at k=(In 2)m/n by calculus. f=Pr[false pos]=0.61285mlm 9
9 False positive probability Assumption: We have good hash functions, look random. Given m bits for filter and n elements, choose number k of hash functions to minimize false positives: Let Let As k increases, more chances to find a 0, but more 1’s in the array. Find optimal at k = (ln 2) m / n by calculus. kn kn m p m e / Pr[cell is empty ] ( 1 1 / ) k kn m k f Pr[false pos ] ( 1 p ) ( 1 e ) / / Pr[false pos] 0.61285m n f
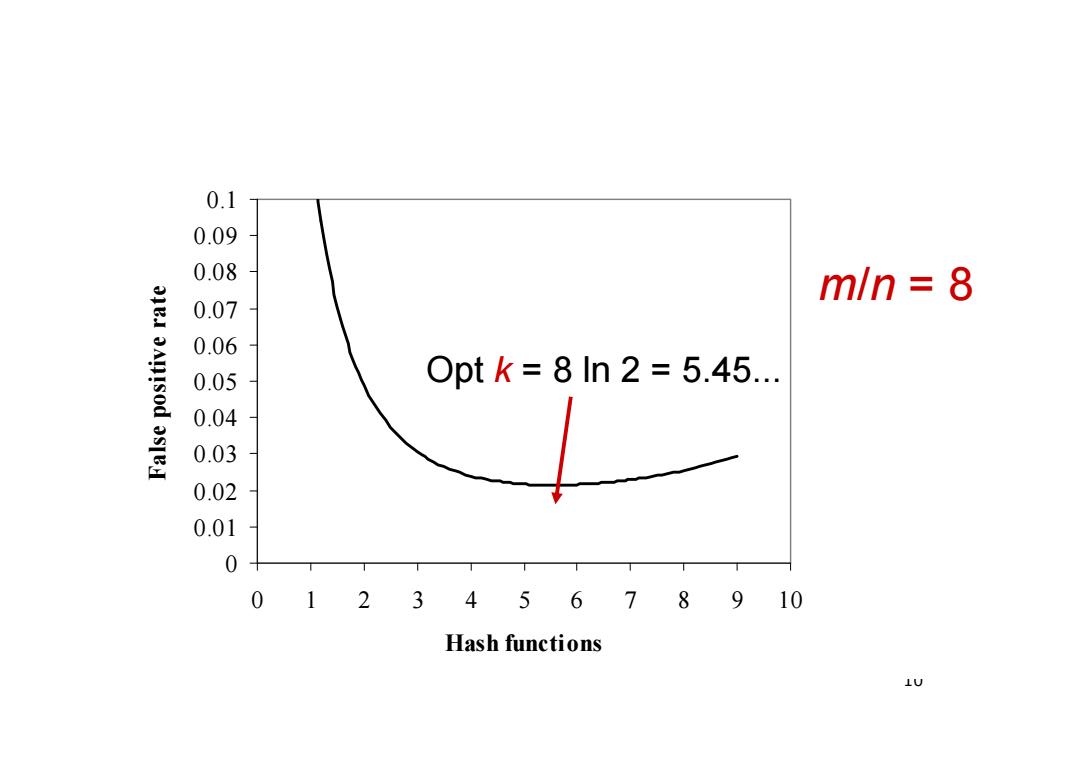
0.1 0.09 0.08 0JEI m/n=8 0.07 0.06 0.05 0ptk=8ln2=5.45.. 0.04 OSIEH 0.03 0.02 0.01 0 012345678910 Hash functions 10
10 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0 1 2 3 4 5 6 7 8 9 10 Hash functions False positive ratem/n = 8 Opt k = 8 ln 2 = 5.45