线性动态电路的夏频域分折山-例 求: f(t)=te(t)和f(t)=t'c(t)的象函数解L[te(t)] = L[/_ 8(t)dt] =---L[t’ε(t)]= L[2 [" tdt] =返上回页下页
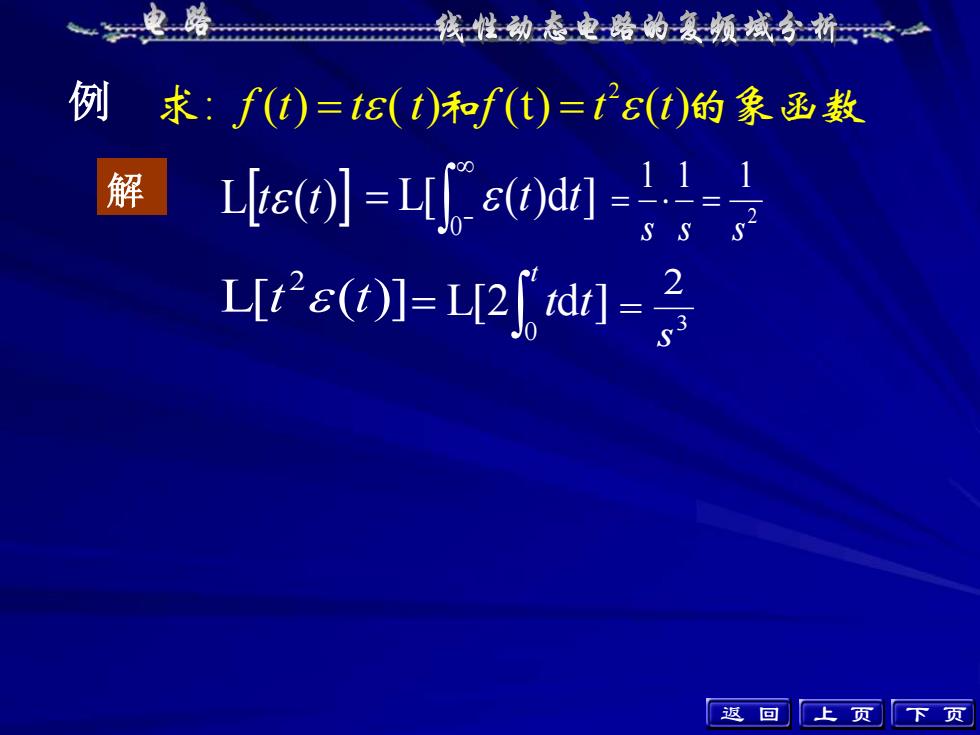
求: f (t) = t (t)和f (t) = t 2 (t)的象函数上 页 下 页 L[2 d ] 0 = t t t 例 Lt (t) 2 1 1 1 s s s L[ ( )d ] = = 0 − = t t L[ ( )] 2 t t 3 2 s = 解 返 回

电路线性动态电路的夏频域分折山4.延迟性质则 : L[f(t-to)c(t-to)]=e-s% F(s)若: LLf(t)l= F(s)证L[f(t-to)e(t-to)]= (f(t-to)e(t-to)e-"'dt.令 t-to =tf(t-to)e-stdt-sto-s(t+to)f(t)e-stdt'dt=ef(t)e0= e-sto F(s)e-sto延迟因子返上回页下页
4.延迟性质 f t t e t st t ( ) d 0 0 − = − ( ) 0 e F s −st = 若: L[ f (t)] = F(s) L[ ( ) ( )] ( ) 0 0 0 f t t t t e F s −s t 则: − − = f t t t t f t t t t e t s t L ( ) ( ) ( ) ( ) d 0 0 0 0 0 − − − − = − − ( ) d 0 ( ) 0 − + − = s t f e − = 0 令 t t e −st0 延迟因子 上 页 下 页 证 ( ) d 0 0 − − − = st s e f e 返 回

线性动态电路的夏频域分折山例1求矩形脉冲的象函数Z解f(t)=ε(t) -ε(t -T)-S7根据延迟性质F(s-f(t)SS例2求三角波的象函数解f(t)=tlε(t)-(t-T)f(t)=ts(t)-(t -T)s(t -T)- T(t -T)T-ST-STF(s)OSS返上回页个页
例1 f (t) = (t) − (t −T) T F e s s 1 s 1 (s) − = − f (t) = t[ (t) − (t −T)] f (t) = t (t) − (t −T) (t −T) −T (t −T) T T e T F e s s 2 2 s s 1 s 1 (s) − − = − − 例2 求矩形脉冲的象函数 解 根据延迟性质 求三角波的象函数 解 上 页 下 页 T T f(t) o 1 T t f(t) o 返 回

线性动态电路的夏频域分折山(t)例3求周期函数的拉氏变换解设f(t)为一个周期的函数LLf(t))= F(s)0T/2 T: f(t)= f(t)+ f(t -T)c(t -T) +fi(t -2T)e(t -2T)+...L[f(t)= F(s)+e-sT F(s)+e-2sT F(s)+..= F(s)[e-sT +e-2sT0-3sTF(s)te+.-ST返上回页下页
求周期函数的拉氏变换 设f1 (t)为一个周期的函数 − − + = + − − + ( 2 ) ( 2 ) ( ) ( ) ( ) ( ) 1 1 1 f t T t T f t f t f t T t T ( )[ ] 2 3 1 = + + + −sT − sT − sT F s e e e ( ) 1 1 1 F s e −sT − = 例3 解 L[ ( )] ( ) 1 1 f t = F s = + + + − − L[ ( )] ( ) ( ) ( ) 1 2 1 1 f t F s e F s e F s s T s T 上 页 下 页 . t f(t) 1 o T/2 T 返 回

线性动态电路的夏频域分折山L[f(t)]F(s)STf, (t) = ε(t)-ε(t -对于本题脉冲序列LLf(t))-ST5.拉普拉斯的卷积定理若: L[f(t)}=F(s)L[f,(t))= F(s)返上回页F页
) s 1 s 1 (s) ( s / 2 1 T F e − = − ) 2 ( ) ( ) ( 1 T f t = t − t − ) 1 1 ( 1 sT / 2 s e − + = ( ) 1 1 L[ ( )] 1 F s e f t −s T − = ) 1 1 ( 1 1 s T / 2 s T e e s s − − − − L[ f (t)] = 上 页 下 页 对于本题脉冲序列 5.拉普拉斯的卷积定理 L[ ( )] ( ) L[ ( )] ( ) 1 1 2 2 若: f t = F s f t = F s 返 回