
全程设计 7.4 数学建模活动:周期现象的描述
7.4 数学建模活动: 周期现象的描述

导航 课标定位 素养阐释 1.了解常见的周期现象. 2.能借助于合适的仪器,采集数据,建立数学模型,分析研究周 期现象 3.加强数据分析、数学运算、逻辑分析能力的培养
导航 课标定位 素养阐释 1.了解常见的周期现象. 2.能借助于合适的仪器,采集数据,建立数学模型,分析研究周 期现象. 3.加强数据分析、数学运算、逻辑分析能力的培养

导月 数学建模 完整的数学建模活动一般要经历选题、开题、做题、结题四 个过程 1选题是指根据要求选定合适的研究对象的过程 2.开题是指讨论与确定建模步骤的过程. 3.做题是指按照讨论的步骤进行实际建模的过程 4.结题是指总结与交流的过程
导航 一、数学建模 完整的数学建模活动一般要经历选题、开题、做题、结题四 个过程. 1.选题是指根据要求选定合适的研究对象的过程. 2.开题是指讨论与确定建模步骤的过程. 3.做题是指按照讨论的步骤进行实际建模的过程. 4.结题是指总结与交流的过程

二、建立数学模型解决实际问题 导航 【例题】[发现问题,提出问题] 一个地区在不同日子中白昼的时长是不同的,下表是某地一 年中10天测量的白昼时长统计表(时间近似到0.1h). 日期 1月 2月 B月 4月 5月 6月 8月 9月 10月 12月 1日 28日 21日 27日 6日 21日 13日 20日 25日 21日 日期位 置编号 59 180 117 126 172 225 263 298 355 x 白昼时 长yh 5.6 10.2 12.4 16.4 17.3 19.4 16.4 12.4 8.5 5.4
导航 二、建立数学模型解决实际问题 【例题】 [发现问题,提出问题] 一个地区在不同日子中白昼的时长是不同的,下表是某地一 年中10天测量的白昼时长统计表(时间近似到0.1 h). 日期 1月 1日 2月 28日 3月 21日 4月 27日 5月 6日 6月 21日 8月 13日 9月 20日 10月 25日 12月 21日 日期位 置编号 x 1 59 80 117 126 172 225 263 298 355 白昼时 长y/h 5.6 10.2 12.4 16.4 17.3 19.4 16.4 12.4 8.5 5.4
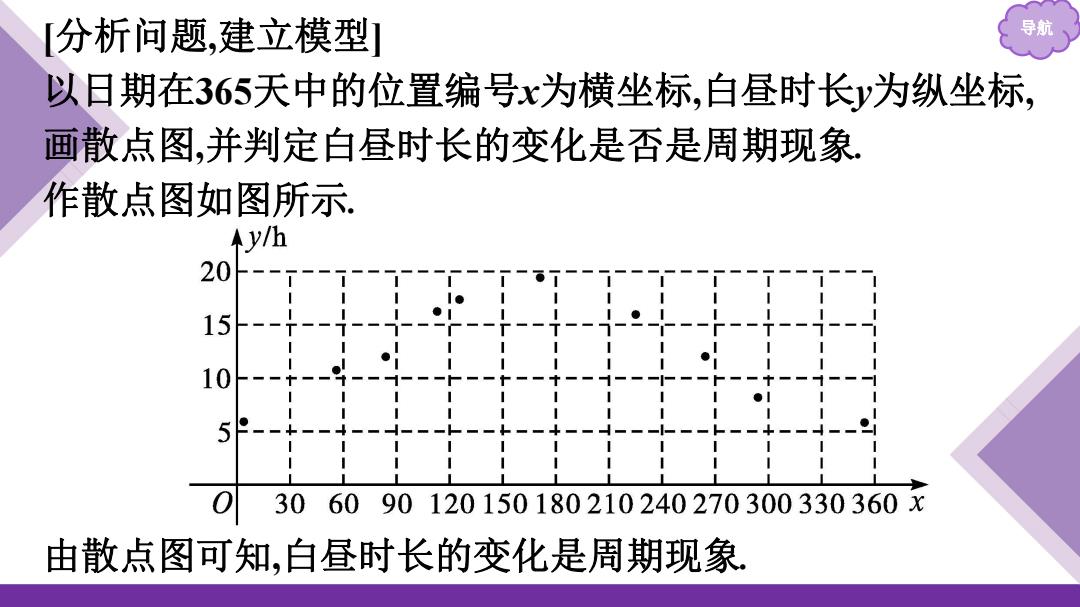
[分析问题,建立模型] 以日期在365天中的位置编号x为横坐标,白昼时长y为纵坐标, 画散点图,并判定白昼时长的变化是否是周期现象, 作散点图如图所示 Ay/h 20 15 10 5 30 6090120150180210240270300330360x 由散点图可知,白昼时长的变化是周期现象
导航 [分析问题,建立模型] 以日期在365天中的位置编号x为横坐标,白昼时长y为纵坐标, 画散点图,并判定白昼时长的变化是否是周期现象. 作散点图如图所示. 由散点图可知,白昼时长的变化是周期现象