例2向[0,1]区间随机抛一质点,以X表示质点坐 标.假定质点落在[0,1]区间内任一子区间内的概率 与区间长成正比,求X的分布函数 解:Fx)=P{X≤x F(x) 当x<0时,F(x)=0;当x>1时,F(x)=1 当0≤≤1时,F(x)=P{0≤X≤x=kxI 特别,F(1))=P{0≤x≤1}=k=1 0, x<0 ∴.F(x)=P(X≤x)=x, 0≤x≤1 1, x>1
例2 向[0,1]区间随机抛一质点,以X表示质点坐 标.假定质点落在[0,1]区间内任一子区间内的概率 与区间长成正比,求X的分布函数 解: F(x)=P{X≤x} 1, 1 , 0 1 0, 0 ( ) ( ) x x x x F x =P X x = F(x) x 0 1 1 当x<0时,F(x)=0;当x>1时,F(x)=1 当0≤x≤1时, F(x) = P{0 X x} = k x 特别,F(1)=P{0≤x≤1}=k=1

用分布函数描述随机变量不如分布律直观, 对非离散型随机变量,是否有更直观的描述方法? p{a<X≤b}=?
用分布函数描述随机变量不如分布律直观, 对非离散型随机变量,是否有更直观的描述方法? a b p{a X b} = ?

2.4连续型随机变量 一、 概率密度 1.定义p3)对于随机变量X,若存在非负函 数fx),(-oo<<+oo),使对任意实数x,都有 F(x)=P(X≤x)=nf(u)dd 则称X为连续型随机变量,x)为X的概率 密度函数,简称概率密度或密度函数: 常记为 X~fX),(-0<x<+o)
2.4 连续型随机变量 一、概率密度 1. 定义(p33) 对于随机变量X,若存在非负函 数f(x),(-<x<+),使对任意实数x,都有 − x F(x)=P(X x)= f (u)du 则称X为连续型随机变量, f(x)为X的概率 密度函数,简称概率密度或密度函数. 常记为 X~ f(x) , (-<x<+)
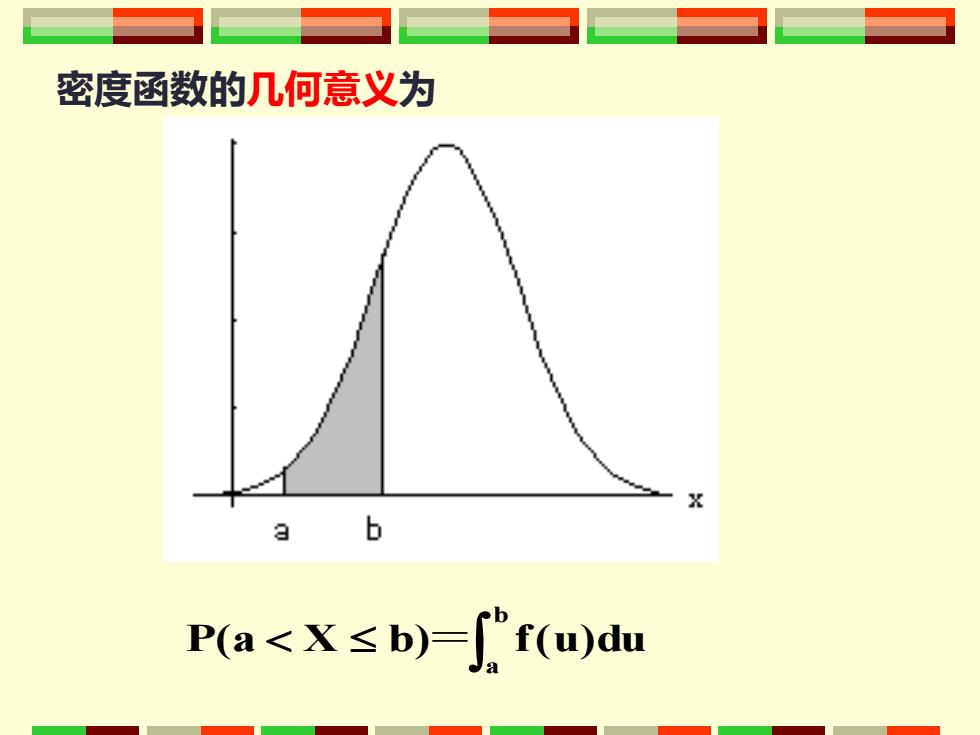
密度函数的几何意义为 b P(a<X≤b)="f(u)du
密度函数的几何意义为 b a P(a X b)= f(u)du

2. 密度函数的性质(p34) (1)非负性fx)≥0,(o<x<o): (2)归一性 mf(x)d=1. 性质(1)、(2)是密度函数的充要性质: 设随机变量X的概率套度为 f(x)=ae 答 求常数a, 1 a= 2
2. 密度函数的性质 (p34) (1) 非负性 f(x)0,(-<x<); (2)归一性 ( ) =1. + − f x dx 性质(1)、(2)是密度函数的充要性质; x f x ae − ( ) = 设随机变量X的概率密度为 求常数a. 答: 2 1 a =