
例3.从某大学到火车站途中有6个交通岗,假设在各个 交通岗是否遇到红灯相互独立,并且遇到红灯的概率 都是1/3. (1)设X为汽车行驶途中遇到的红灯数,求X的分布律。 (2)求汽车行驶途中至少遇到5次红灯的概率 解:(1)由题意,X~B(6,1/3),于是,X的分布律为: -C k=0,1.,6 (2)P{X≥5}=P{X=5}+P{X=6} c)0 729
例3.从某大学到火车站途中有6个交通岗,假设在各个 交通岗是否遇到红灯相互独立,并且遇到红灯的概率 都是1/3. (1)设X为汽车行驶途中遇到的红灯数,求X的分布律. (2)求汽车行驶途中至少遇到5次红灯的概率. 解:(1)由题意,X~B(6,1/3),于是,X的分布律为: 0,1,.,6 3 2 3 1 { } 6 6 = = = − P X k C k k k k (2) P{X 5}= P{X = 5}+ P{X = 6} 729 13 3 1 3 2 3 1 5 6 5 6 = + = C

例4.某人射击的命中率为0.02,他独立射击400 次,试求其命中次数不少于2的概率。 解 设X表示400次独立射击中命中的次数, 则XB(400,0.02),故 P{X≥2}=1-P{X=0}-P{X=1 =1-0.9840-(400)(0.02)(0.98399)=. 泊松定理(p28)设随机变量Xn~B(n,p),(n=0,1, 2,.),且n很大,p很小,记入=np,则 P{X=k}≈ -e- k=0,1,2
例4. 某人射击的命中率为0.02,他独立射击400 次,试求其命中次数不少于2的概率。 泊松定理(p28) 设随机变量Xn~B(n, p), (n=0, 1, 2,.), 且n很大,p很小,记=np,则 , 0,1,2,. ! { = } = − e k k P X k k 解 设X表示400次独立射击中命中的次数, 则X~B(400, 0.02),故 P{X2}=1- P{X=0}-P {X=1} =1-0.98400-(400)(0.02)(0.98399)=

上题用泊松定理取入=np=(400)(0.02)=8,故 近似地有 P{X≥2}=1-P{X=0}-P{X=1} =1-(1+8)e8=0.996981. (二.)泊松(Poisson)分布P()p28) k X~PX=k}=e元,k=0,1,2, k (2>0)
上题用泊松定理 取 =np=(400)(0.02)=8, 故 近似地有 P{X2}=1- P{X=0}-P {X=1} =1-(1+8)e-8=0.996981. (二. ) 泊松(Poisson)分布P()(p28) X~P{X=k}= , k=0, 1, 2, . (0) − e k! k
泊松定理表明,泊松分布是二项分布的极限分布, 当n很大,p很小时,二项分布就可近似地 看成是参数)=np的泊松分布 0.35 B(10.3/20) 0.3 二项分布B(10,3/20)的泊松近似P(312) 0.29 P(3/2) 0.15 0.1 0.05
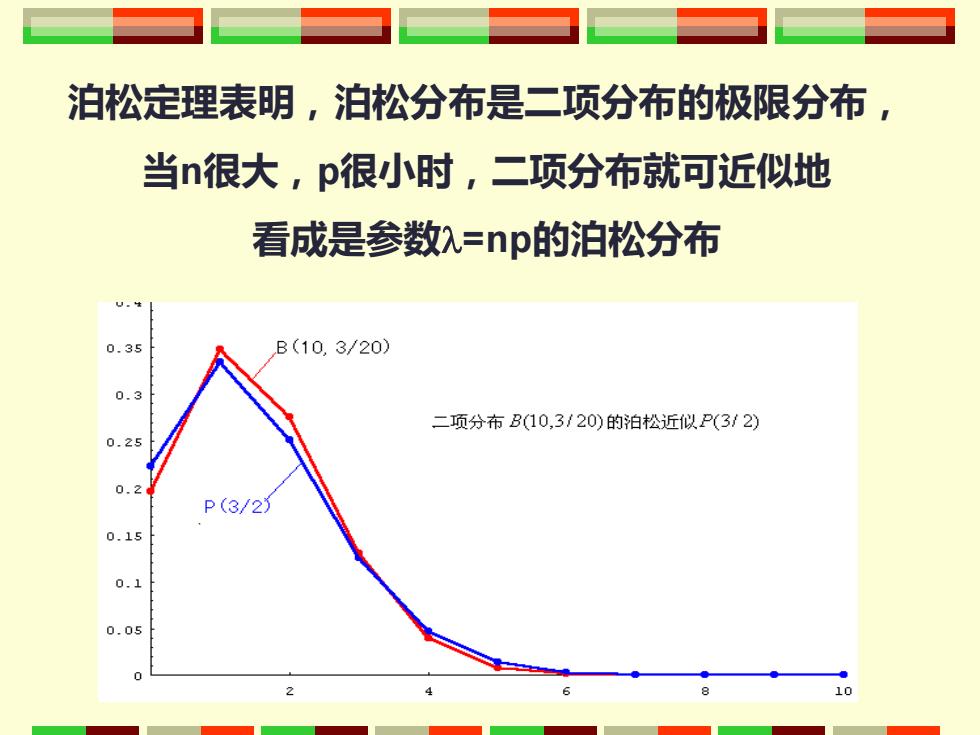
泊松定理表明,泊松分布是二项分布的极限分布, 当n很大,p很小时,二项分布就可近似地 看成是参数=np的泊松分布

例5.设某国每对夫妇的子女数X服从参数为入的泊松 分布,且知一对夫妇有不超过1个孩子的概率为3e2.求 任选一对夫妇至少有3个孩子的概率。 解:由题意, X~p(2),且PX≤1)=P{X=0}+P{X=1}=32 e2+e=3e2→1=2 P{X≥3}=1-P{X=0}-P{X=1}-P{X=2 =1-d-7e-e-1-002
例5.设某国每对夫妇的子女数X服从参数为的泊松 分布,且知一对夫妇有不超过1个孩子的概率为3e-2 .求 任选一对夫妇,至少有3个孩子的概率。 ( ) 2 ~ ( ), 1 { 0} { 1} 3 − X p 且P X = P X = + P X = = e P{X 3}=1−P{X = 0}−P{X =1}−P{X = 2} 1 5 0.323 2! 2 1! 2 1 2 2 2 2 1 2 = − − − = − − − − − e e e e 解:由题意, 3 2 2 + = = − − − e e e