力东理王大彩 SHANDONG UNIVERSITY OF TECHNOLOGY 任意可逆循环分为小Carnot循环 27 2025/4/2
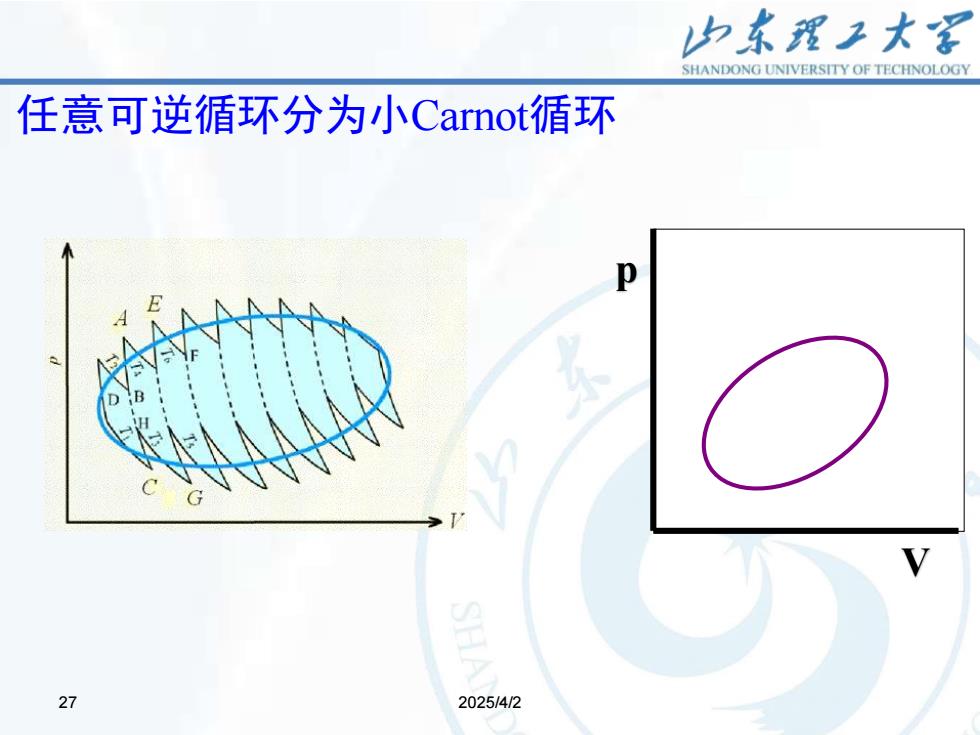
27 2025/4/2 27 任意可逆循环分为小Carnot循环 p V

口东理王大 SHANDONG UNIVERSITY OF TECHNOLOGY 802+ 0 =0 d24+d0 =0 T 606 62 二0 To T + +δ2+d0+.=0 T %.=0到2 =0 28 2025/4/2
28 28 2025/4/2 2 1 2 1 0 Q Q T T + = 4 3 4 3 0 Q Q T T + = 6 5 6 5 0 Q Q T T + = 1 2 4 3 1 2 3 4 0 Q Q Q Q T T T T + + + + = R ( ) 0 i i iQT = R δ 0 QT =

2.熵的引出 归东理工大 SHANDONG UNIVERSITY OF TECHNOLOGY 用一闭合曲线代表任意可逆循环。 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式: 9-0 将上式分成两项的加和 R (9+0(9-0 B 任意可逆循环 29 2025/4/2
29 2025/4/2 29 用一闭合曲线代表任意可逆循环。 1 2 B A R R A B ( ) ( ) 0 Q Q T T + = 将上式分成两项的加和 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式: 0 δ R = T Q 2.熵的引出
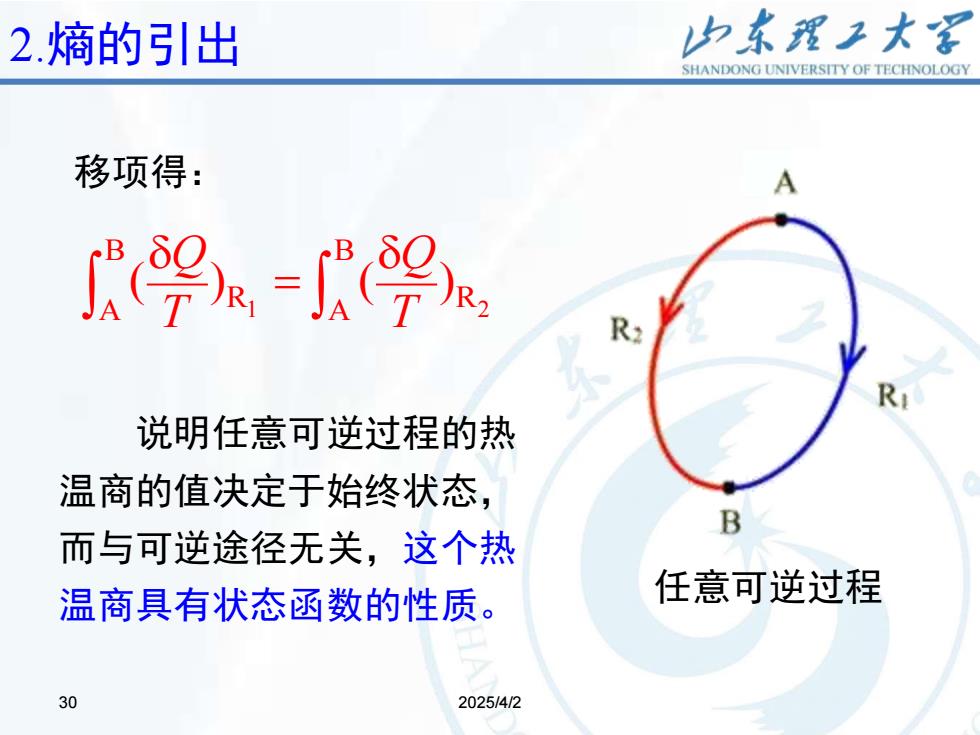
2.熵的引出 归东理子大名 SHANDONG UNIVERSITY OF TECHNOLOGY 移项得: A 9=R9 说明任意可逆过程的热 温商的值决定于始终状态, 而与可逆途径无关,这个热 温商具有状态函数的性质。 任意可逆过程 30 2025/4/2
30 2025/4/2 30 2.熵的引出 说明任意可逆过程的热 温商的值决定于始终状态, 而与可逆途径无关,这个热 温商具有状态函数的性质。 移项得: 1 2 B B R R A A ( ) ( ) Q Q T T = 任意可逆过程

3.熵的定义 力东理子大 SHANDONG UNIVERSITY OF TECHNOLOGY Clausiusz根据可逆过程的热温商值决定于始终态而 与可逆过程无关这一事实定义了“熵”(entropy) 这个函数,用符号“S表示,单位为:JK 设始、终态A,B的熵分别为Sa和S,则: S-S,=心=j9。 或 =Σ2.人△w-Σ%=0 对微小变化 这几个熵变的计算式习惯上称为熵的定义式, 即熵的变化值可用可逆过程的热温商值来衡量
31 31 2025/4/2 3.熵的定义 Clausius根据可逆过程的热温商值决定于始终态而 与可逆过程无关这一事实定义了“熵”(entropy) 这个函数,用符号“S” 表示,单位为: 1 J K− d ( )R Q S T 对微小变化 = 这几个熵变的计算式习惯上称为熵的定义式, 即熵的变化值可用可逆过程的热温商值来衡量。 B B A R A ( ) Q S S S T − = = R ( ) 0 i i i Q S T ( )R − = i i i Q S T 或 = 设始、终态A,B的熵分别为 SA 和 SB ,则: