
§2.5 Clausius不等式与熵增加原理中东罗2大 HANDONG UNIVERSITY OF TECHNOLOGY Clausius不等式 热力学第二定律的数学表达式 熵增加原理 32 2025/4/2
32 2025/4/2 32 §2.5 Clausius 不等式与熵增加原理 Clausius 不等式—— 热力学第二定律的数学表达式 熵增加原理

Clausius不等式 力东理子大 SHANDONG UNIVERSITY OF TECHNOLOGY 设温度相同的两个高、低温热源间有一个可逆 热机和一个不可逆热机。 根据Carnot定理: -W_9+9<T-T 92 92 T +9<0 不可逆循环热温商之和小于零 推广为与n个热源接触的任意不可逆过程,得: 33 2025/4/2
33 2025/4/2 33 Clausius 不等式 设温度相同的两个高、低温热源间有一个可逆 热机和一个不可逆热机。 根据Carnot定理: I 0 0 n i i i Q T < 推广为与n个热源接触的任意不可逆过程,得: 2 1 2 1 2 2 2 I W Q Q T T Q Q T − + − = = 0 2 2 1 1 + T Q T Q 不可逆循环热温商之和小于零
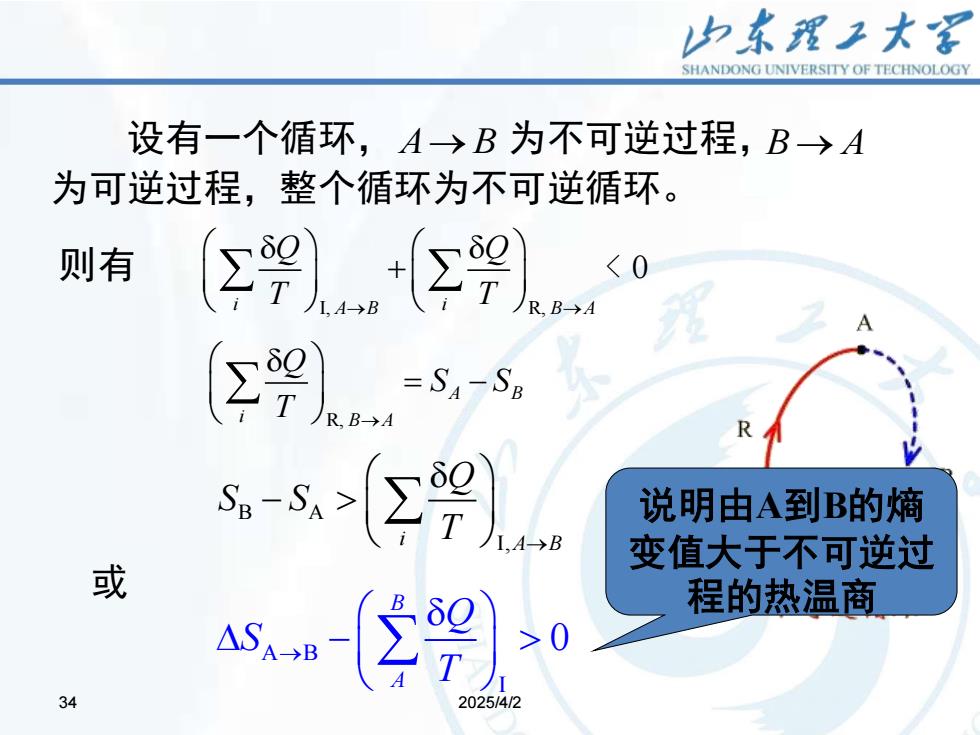
归东理子大名 SHANDONG UNIVERSITY OF TECHNOLOGY 设有一个循环,A→B为不可逆过程,B→A 为可逆过程,整个循环为不可逆循环。 则有 Σ9{2¥ <0 R,B→A 9) 89 说明由A到B的熵 变值大于不可逆过 或 a58-29)20 程的热温商 34 2025/4/2
34 2025/4/2 34 R, A B i B A Q S S T → = − A B I 0 B A Q S T → − 或 B A I , i A B Q S S T → − 设有一个循环, 为不可逆过程, 为可逆过程,整个循环为不可逆循环。 A B → B A → I, R, 0 i i A B B A Q Q T T → → + 则有 < 说明由A到B的熵 变值大于不可逆过 程的热温商

力东理子大 SHANDONG UNIVERSITY OF TECHNOLOGY 如A→B为可逆过程 A a故Σ9 =0 RA-B 将两式合并得Clausius不等式: IR B 不可逆循环 δQ是实际过程的热效应,T是环境温度。 若是不 可逆过程,用“>”号,可逆过程用“=”号, 这时 环境与系统温度相同。 2025/4/2
35 2025/4/2 35 如A→B为可逆过程 A B R,A B 0 i Q S T → → − = A B A B ( ) 0 i Q S T → → − 将两式合并得Clausius 不等式: 是实际过程的热效应,T是环境温度。若是不 可逆过程,用“>”号,可逆过程用“=”号,这时 环境与系统温度相同。 Q
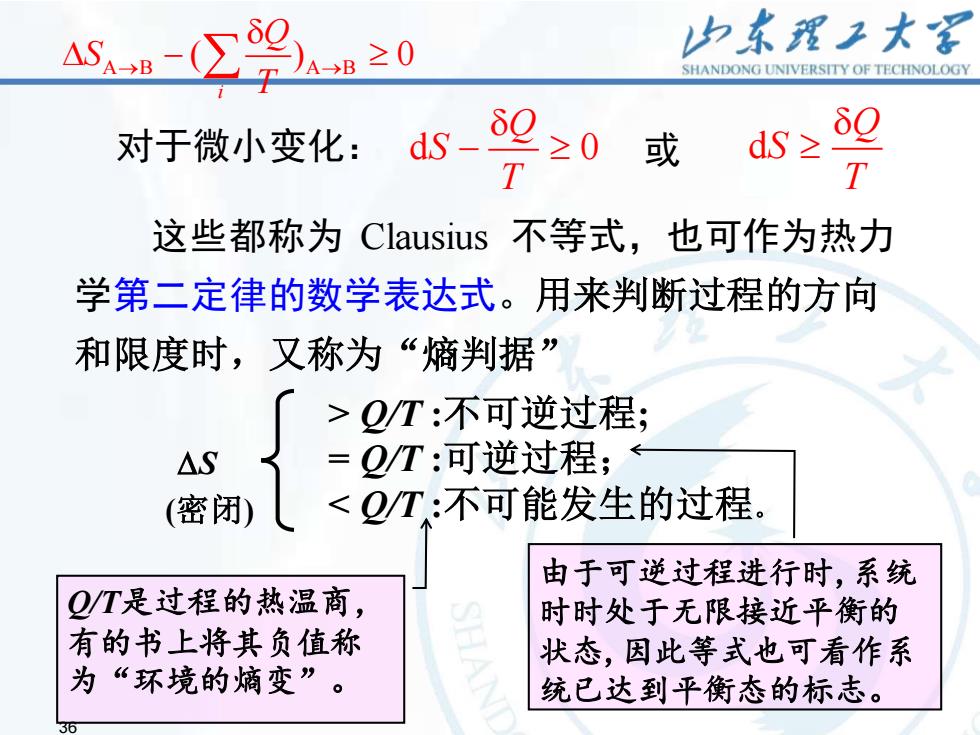
AB≥0 力东强王大 SHANDONG UNIVERSITY OF TECHNOLOGY 对于微小变化: ds- 2≥0 或 dS≥ 60 这些都称为Clausius不等式,也可作为热力 学第二定律的数学表达式。用来判断过程的方向 和限度时,又称为“熵判据” >Q/T:不可逆过程; AS = Q/T:可逆过程; (密闭) <2/T:不可能发生的过程。 由于可逆过程进行时,系统 Q/T是过程的热温商, 时时处于无限接近平衡的 有的书上将其负值称 状态,因此等式也可看作系 为“环境的嫡变”。 统已达到平衡态的标志
36 36 这些都称为 Clausius 不等式,也可作为热力 学第二定律的数学表达式。用来判断过程的方向 和限度时,又称为“熵判据” d Q S T d 0 或 Q S T 对于微小变化: − A B A B ( ) 0 i Q S T → → − S (密闭) > Q/T :不可逆过程; = Q/T :可逆过程; < Q/T :不可能发生的过程。 由于可逆过程进行时,系统 时时处于无限接近平衡的 状态,因此等式也可看作系 统已达到平衡态的标志。 Q/T是过程的热温商, 有的书上将其负值称 为“环境的熵变”