《线性代数》课程教学资源（试卷习题）强化训练题九（解答）

《线性代数D》强化训练题三解答 一、填空题 (-320） 1.1=-530上： 3.5≤5；4.3,0,8；5.k>5 001/8 二、单项选择题 1.D 2.C, 3.A 4.D5.C 三、计算题 1111 1设D=1234 求元素a,b的代数余子式的值 a b c d 141020 解：元素a的代数余子式的值为 1111100 (-0234=212= 112 =16-12=4 616 410204616 元素b的代数余子式的值为 11110023 (-102*2134=-123= 919 =-(38-27=-11 110201919 2.计算行列式的值 -1-

- 1 - 《线性代数 D》强化训练题三解答 一、填空题 1. 1 3 2 0 5 3 0 0 0 1/8 A −   −   = −      ; 2. 1 2 − ; 3. 1 2 r r  ; 4. 3, 0, 8 ; 5. k  5 二、单项选择题 1. D; 2. C; 3. A; 4. D; 5. C 三、计算题 1. 设 1 1 1 1 1 2 3 4 , 1 4 10 20 D a b c d = 求元素 a b, 的代数余子式的值. 解：元素 a 的代数余子式的值为 3 1 1 1 1 1 0 0 1 2 ( 1) 2 3 4 2 1 2 16 12 4; 6 16 4 10 20 4 6 16 + − = = = − = 元素 b 的代数余子式的值为 3 2 1 1 1 1 0 0 2 3 ( 1) 1 3 4 1 2 3 (38 27) 11. 9 19 1 10 20 1 9 19 + − = − = − = − − = − 2. 计算行列式的值

- a 0 .0 0 a . 0 Di= 0 0 0 . 0 0 0 1 1 1 . 1 1 解：第n+1列乘以1加到第n列，第n列乘以1加到第n-1列，.，第2列乘以1加到第1列， -a1a1 0. 0 01 0.00 -a2 .00 00 .00 得Dn1= 0 0 .00 000.00 . . . . 0 00.-anan 000.0an 1 1 1.11n+1nn-1.21 a =(n+1)-(-1)a+ =(-l)(n+l)aa2.aa a 10-1 -210 3.设A=210 B=031 32-1(002 求(I)AB:(2)AB外：(3)B;(4满足BX=A的矩阵X. (-21-2 解：(1)AB=-451 -690 (2)AB=24 2

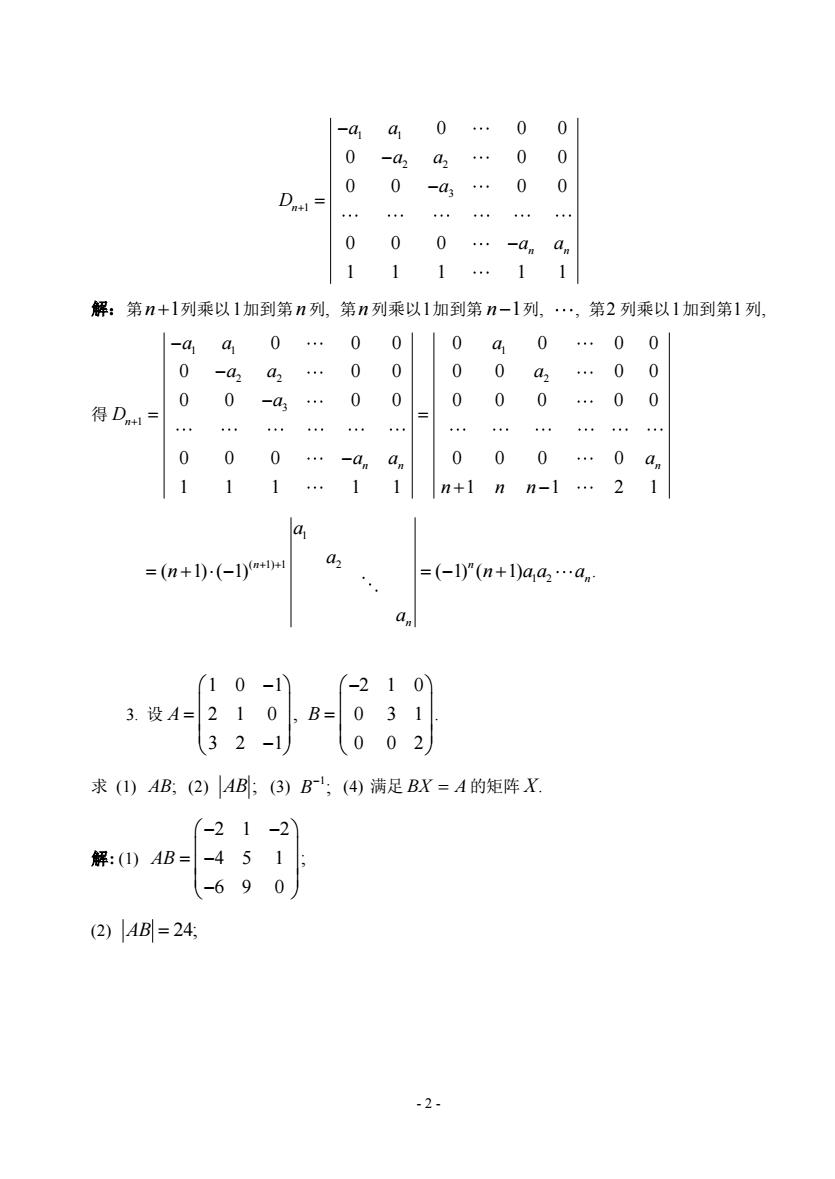
- 2 - 1 1 2 2 3 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 n n n a a a a a D a a + − − − = − 解：第 n+1 列乘以 1 加到第 n 列, 第 n 列乘以 1 加到第 n−1 列, , 第 2 列乘以 1 加到第 1 列, 得 1 1 1 2 2 2 3 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 2 1 n n n n a a a a a a a D a a a n n n + − − − = = − + − 1 ( 1) 1 2 1 2 ( 1) ( 1) ( 1) ( 1) . n n n n a a n n a a a a + + = +  − = − + 3. 设 1 0 1 2 1 0 2 1 0 , 0 3 1 . 3 2 1 0 0 2 A B     − −     = =             − 求 (1) AB; (2) AB ; (3) 1 B ; − (4) 满足 BX A = 的矩阵 X. 解: (1) 2 1 2 4 5 1 ; 6 9 0 AB   − −   = −      − (2) AB = 24;

(11-1 2612 (3)B1= 0 1 1 3 6 0 0 (1 2 0 (4)=BA= 1-6 0 2x+x2-3x=-5 4.问入为何值时，方程组，+3x2-x3=入有解，无解，有解时求全部解 -7x-11x2+9x,=2 2 1-3-5）13-1 解：(Ab)=13-11→0-5-1-5-22 -7-1192200022+31-10 13-1 →0-5-1-5-21 000(2+5元-2) 当1≠2且1≠-5时，R(A)=2≠R(Ab)=3,无解 当=2时， 13-12)1801118011 (Ab)→0-5-1-9 →0-5-1-9→0519 (0000 00000000 -8)11 R(A)=2=R(Ab),有解，通解x=乃 1+0 -59 当1=-5时， -3

- 3 - (3) 1 1 1 1 2 6 12 1 1 0 ; 3 6 1 0 0 2 B −   − −       = −         (4) 1 1 7 0 2 12 1 1 0 . 6 6 3 1 1 2 2 X B A−   −      = =       −   4. 问  为何值时, 方程组 1 2 3 1 2 3 2 1 2 3 2 3 5 3 7 11 9 x x x x x x x x x    + − = −   + − =  − − + = 有解, 无解, 有解时求全部解. 解: 2 2 2 1 3 5 1 3 1 ( ) 1 3 1 0 5 1 5 2 7 11 9 0 0 0 3 10 A     − − −     = − → − − − −             − − + −       b 1 3 1 0 5 1 5 2 0 0 0 ( 5)( 2)   −   → − − − −       + −     当   2 且  −5 时, R A R A ( ) 2 ( ) 3, =  = b 无解; 当  = 2 时, 1 3 1 2 1 8 0 11 1 8 0 11 ( ) 0 5 1 9 0 5 1 9 0 5 1 9 0 0 0 0 0 0 0 0 0 0 0 0 A       −       → − − − → − − − →                   b , R A R A ( ) 2 ( ), = = b 有解, 通解 8 11 1 0 ; 5 9 k     −     = +             − x 当  =−5 时

13-1-5)180-10180-10 u→0-5-150-5-15051-5 000000000000 R(A)=2=R(Ab),有解，通解x=人 四、简答题 1.设A,B均为n阶对称阵，问AB是否也是对称阵？你能否给出AB也是对称阵的充要 条件 解：不一定.充要条件时AB=BA 2.问空间R中的平面2x-3y+:=0是否构成R3中的子空间？若是，求该子空间的基 与维数，若不是，则说出理由 312)-1/2 解：是.dimV=2, 五、已知二次型∫=2x+3x+3x+2ax2X(a>0)可通过正交变换化为标准形 f=y2+2+5y. 1.写出二次型∫=2x+3x+3.x+2ax2x(a>0)的矩阵A和标准形 ∫=y2+2y+5y的矩阵B: 2.由A与B的关系求A的特征值和参数a的值： 3.求正交变换矩阵P. (200(100 解：1.A=03a,B=020 0a3(005 2.因为A与B相似，所以A与B的行列式相等且有相同的特征值，故 4

- 4 - 1 3 1 5 1 8 0 10 1 8 0 10 ( ) 0 5 1 5 0 5 1 5 0 5 1 5 0 0 0 0 0 0 0 0 0 0 0 0 A       − − − −       → − − → − − → −                   b , R A R A ( ) 2 ( ), = = b 有解, 通解 8 10 1 0 . 5 5 k     − −     = +             − − x 四、简答题 1. 设 A B, 均为 n 阶对称阵, 问 AB 是否也是对称阵? 你能否给出 AB 也是对称阵的充要 条件. 解: 不一定. 充要条件时 AB BA = ; 2. 问空间 3 R 中的平面 2 3 0 x y z − + = 是否构成 3 R 中的子空间? 若是, 求该子空间的基 与维数, 若不是, 则说出理由. 解: 是. dim 2, V = 基为 3/ 2 1/ 2 1 0 . 0 1                     － , 五、已知二次型 222 1 2 3 2 3 f x x x ax x a = + + +  2 3 3 2 ( 0) 可通过正交变换化为标准形 2 2 2 1 2 3 f y y y = + + 2 5 . 1. 写出二次型 222 1 2 3 2 3 f x x x ax x a = + + +  2 3 3 2 ( 0) 的矩阵 A 和标准形 2 2 2 1 2 3 f y y y = + + 2 5 的矩阵 B; 2. 由 A 与 B 的关系求 A 的特征值和参数 a 的值; 3. 求正交变换矩阵 P. 解: 1. 2 0 0 1 0 0 0 3 , 0 2 0 . 0 3 0 0 5 A a B a         = =             2. 因为 A 与 B 相似, 所以 A 与 B 的行列式相等且有相同的特征值, 故

200100 03a=020 即2(9-a2)=10,所以a=2. 0a3005 且由于B的特征值为1,2,5，所以A的特征值也为1,2,5 0 0 3.=15= 1 1 P= 1 1 1 =2,5=0=0 0 0 0 1 =5,5=-1 -1 1 050 所以正交变换矩阵P=(B,P2,P)= 1 10 -1 101 六、证明题 1.已知a,a2,a3是线性空间V的一个基，设 月=a+2a2+a,月2=2a+3a+3a,月=3a+7a%-a 证明B,B,B也是V的一个基，并求基，a2,a到基月，B,B的过渡矩阵。 (123Y 证：(B,月，月)=(a,aa)237 13-1 123 因为237≠0， 所以B,B,B线性无关，则也是V的一个基.显然过渡矩阵就是 13-1 -5

- 5 - 2 0 0 1 0 0 0 3 0 2 0 , 0 3 0 0 5 a a = 即 2 2(9 ) 10, − = a 所以 a = 2. 且由于 B 的特征值为 1, 2, 5, 所以 A 的特征值也为 1, 2, 5. 3. 1 1 1 0 0 1 1, 1 , 1 , 2 1 1          = = =              p 2 2 2 1 1 2, 0 , 0 , 0 0          = = =              p 3 3 3 0 0 1 5, 1 , 1 , 2 1 1          = = − = −              p 所以正交变换矩阵 1 2 3 0 2 0 1 ( , , ) 1 0 1 . 2 1 0 1 P     = = −       p p p 六、证明题 1. 已知 1 2 3    , , 是线性空间 V 的一个基, 设 1 1 2 3     = + + 2 , 2 1 2 3     = + + 2 3 3 , 3 1 2 3     = + − 3 7 . 证明 1 2 3    , , 也是 V 的一个基, 并求基 1 2 3    , , 到基 1 2 3    , , 的过渡矩阵. 证: 1 2 3 1 2 3 1 2 3 ( , , ) ( , , ) 2 3 7 , 1 3 1     =       −       因为 1 2 3 2 3 7 0, 1 3 1  − 所以 1 2 3    , , 线性无关, 则也是 V 的一个基. 显然过渡矩阵就是