
线性代数学习指导 行列式 一、内容提要 1.排列的逆序数:排列户P2P的逆序数 1=4+4++,=2 其中1,为元素P,的逆序数。逆序数为奇数的排列为奇排列,逆序数为偶数的排列为偶排列。 2.对换:一次对换改变排列的奇偶性。 3.n阶行列式的定义 (1)二阶行列式 ldn dudnd-dhada az az (2)三阶行列式 a21a2a23=a11a2a3+a3421a2+a12a23431-a12421a3-4ia23432-a1342a31 a an as (3)n阶行列式 a1a2.an . an1an2.anm 其中1为排列PP2.P的逆序数 4.行列式的性质 性质1:行列式与其转置行列式相等。 性质2:交换行列式的任意两行(或列),行列式改变符号。特别地,如果行列式有两 行(或列)对应元素相等或成比例,则行列式为零。 性质3:如果行列式的某一行(或列)有公因子,则该公因子可提到行列式记号外面来。 性质4:如果行列式的某一行(或列)为两组数之和,则该行列式可以分解为两个行列 式之和。注意改变的仅仅是该行(或列),其他行(或列)不变。 性质5:把行列式的某一行(或列)乘以一个常数加到另一行(或列)上去,行列式的 值不变。 5.行列式按行(或列)展开定理 det(ay)=+++=1.2.,n deta)=ayA,+a2,A,+.+awAn,j=l,2,.,n
线性代数学习指导 行列式 一.内容提要 1.排列的逆序数:排列 p1 p2 pn 的逆序数 = = + + + = n i n i t t t t t 1 1 2 其中 i t 为元素 i p 的逆序数。逆序数为奇数的排列为奇排列,逆序数为偶数的排列为偶排列。 2.对换:一次对换改变排列的奇偶性。 3. n 阶行列式的定义 (1)二阶行列式 11 22 12 21 21 22 11 12 a a a a a a a a = − (2)三阶行列式 1 1 2 2 3 3 1 3 2 1 3 2 1 2 2 3 3 1 1 2 2 1 3 3 1 1 2 3 3 2 1 3 2 2 3 1 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 a a a a a a a a a a a a a a a a a a a a a a a a a a a = + + − − − (3) n 阶行列式 = = − = − p p p n t p p p p p n p t n n n n n n i j n n n a a a a a a a a a a a a a a a a 1 2 1 2 1 2 2 1 2 2 2 1 1 1 2 1 1 2 1 2 1 2 det( ) ( 1) ( 1) 其中 t 为排列 p1 p2 pn 的逆序数。 4.行列式的性质 性质 1:行列式与其转置行列式相等。 性质 2:交换行列式的任意两行(或列),行列式改变符号。特别地,如果行列式有两 行(或列)对应元素相等或成比例,则行列式为零。 性质 3:如果行列式的某一行(或列)有公因子,则该公因子可提到行列式记号外面来。 性质 4:如果行列式的某一行(或列)为两组数之和,则该行列式可以分解为两个行列 式之和。注意改变的仅仅是该行(或列),其他行(或列)不变。 性质 5:把行列式的某一行(或列)乘以一个常数加到另一行(或列)上去,行列式的 值不变。 5.行列式按行(或列)展开定理 det(aij) = ai1A1 j + ai2 A2 j ++ ai nAnj ,i = 1,2, ,n ; 或 det(aij) = a1 j A1 j + a2 j A2 j ++ anj Anj , j = 1,2, ,n
线性代数学习指导 amAn+a2A2+.amAm=0,i≠j auAy+az Az++a Au =0.ij 其中A,=(-l)M,为元素a,的代数余子式,M为元素an的余子式。 6.特殊行列式的值 (1)对角行列式 =元.元m =(-1)2.n (2)三角行列式 a1a2.an a. =a1a2.am a2 =01122a ,。 a a d2n-1 d2n 2m- a1na2l.an a1.a1w 0 a. (3) b.bn b.bn (4)范德蒙行列式 1 1 1.1 X1 X2 X.x .x =(x2-xx3-(n-xx3-x2)(x。-x2(x。-x) =Πx-x,) 二,典型例题精解 例1一1求排列13(2n-1)2n(2n-2).42的逆序数
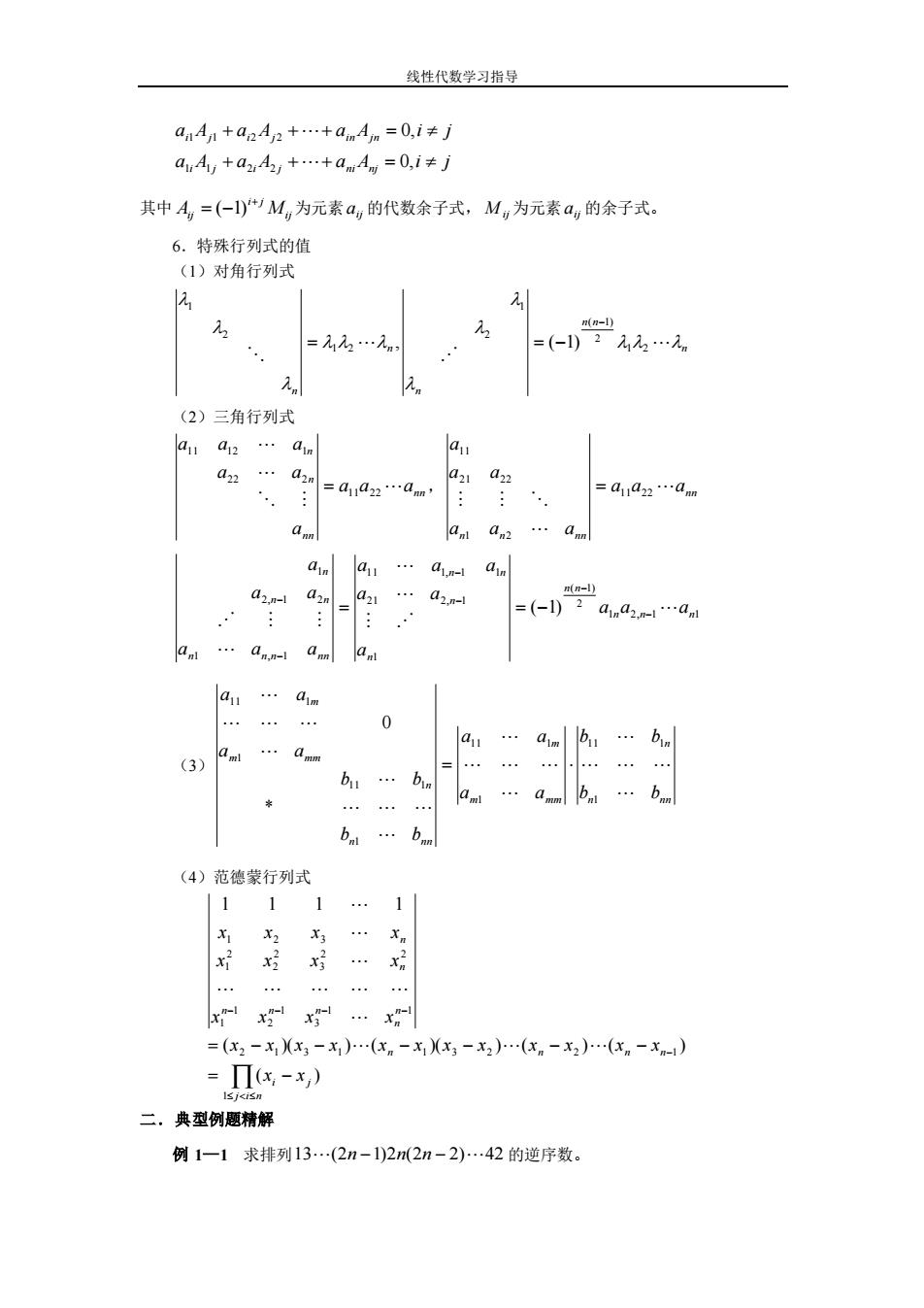
线性代数学习指导 a A a A a A i j a A a A a A i j i j i j ni nj i j i j in jn + + + = + + + = 0, 0, 1 1 2 2 1 1 2 2 其中 ij i j Aij M + = (−1) 为元素 ij a 的代数余子式, M ij 为元素 ij a 的余子式。 6.特殊行列式的值 (1)对角行列式 n n n n n n 1 2 2 ( 1) 2 1 1 2 2 1 , ( 1) − = = − (2)三角行列式 nn nn n n a a a a a a a a a 11 22 22 2 11 12 1 = , nn n n nn a a a a a a a a a 11 22 1 2 21 22 11 = 1 2, 1 1 2 ( 1) 1 2 1 2, 1 1 1 1, 1 1 1 , 1 2, 1 2 1 ( 1) n n n n n n n n n n n n n n n n n a a a a a a a a a a a a a a a − − − − − − = = − (3) n n n n m mm m n n n n m mm m b b b b a a a a b b b b a a a a 1 11 1 1 11 1 1 11 1 1 11 1 * 0 = (4)范德蒙行列式 1 1 3 1 2 1 1 2 2 3 2 2 2 1 1 2 3 1 1 1 1 − − − n− n n n n n n x x x x x x x x x x x x − = − = − − − − − − j i n i j n n n n x x x x x x x x x x x x x x 1 2 1 3 1 1 3 2 2 1 ( ) ( )( )( )( )( )( ) 二.典型例题精解 例 1—1 求排列 13(2n −1)2n(2n − 2)42 的逆序数

线性代数学习指导 【思路分析】元素比较多,找出元素逆序数的规律。 解元素13,.,2n-L2n的逆序数为0: 元素2n-2的逆序数为2: 元素2n-4的逆序数为4: 元素2=2n-(2n-2)的逆序数为2n-2。 所求排列的逆序数 1=0+2+4+.+(2n-2)=n(n-1)。 x113 k134 解方法一:【思路分析】按行列式的定义计算 由行列式的定义,行列式的每一项是不同行与不同列的乘积,得 fx)=(-1)23xx-x.4x+.=4x+ 所以x4的系数为4. 方法二:【用路分析】按行列式展开定理计算 将行列式按第一行展开,得 x2 1 x2 1x x 1 xx 2 fx)=x2x3-1x3+123-12x 134xx34xx14k13到 x21 =2x3+ .=x(4x3+)+.=4x+ 134x 所以x的系数为4。 【注意】解答此类问题一般不要把行列式完全计算出来 例1一3计算四阶行列式 1 -1 1 x-1 D= 1 -1x+1 -1 1x-1 1 -1 x+1-1 1 -1 解方法一:【思路分析】将行列式化成三角行列式
线性代数学习指导 【思路分析】元素比较多,找出元素逆序数的规律。 解 元素 1,3, ,2n −1,2n 的逆序数为 0; 元素 2n − 2 的逆序数为 2 ; 元素 2n − 4 的逆序数为 4 ; . 元素 2 = 2n − (2n − 2) 的逆序数为 2n − 2。 所求排列的逆序数 t = 0 + 2 + 4 ++ (2n − 2) = n(n −1)。 例 1—2 求多项式 x x x x x x f x 1 3 4 1 2 3 2 1 1 1 3 ( ) = 中 4 x 的系数。 解 方法一:【思路分析】按行列式的定义计算 由行列式的定义,行列式的每一项是不同行与不同列的乘积,得 f (x) = (−1) (1234) x x x 4x += 4x 4 + 所以 4 x 的系数为 4。 方法二:【思路分析】按行列式展开定理计算 将行列式按第一行展开,得 1 3 1 2 2 1 4 1 2 3 1 3 4 1 3 2 1 1 3 4 2 3 2 1 ( ) x x x x x x x x x x x x x x x f x = x − + − = + = (4 3 +) + = 4 4 + 1 3 4 2 3 2 1 x x x x x x x 所以 4 x 的系数为 4。 【注意】解答此类问题一般不要把行列式完全计算出来。 例 1—3 计算四阶行列式 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 + − − − − − + − − − = x x x x D 解 方法一:【思路分析】将行列式化成三角行列式

线性代数学习指导 1-11x- 3001-1 0x0-x 010-1 x010 x00-x 100-1 01-1x 1-11x-1 1-11x- -x010-2-x010-l 001 001 -1 01-1-x 00-11-x 1-11x- -x010- 001-1x 000-x 【注意】对于低阶行列式,都可直接化成三角行列式,但这样计算一般都比较麻烦, 只有对某些特殊的行列式直接化成三角行列式才有效。 方法二:【思路分析】行列式的每列元素之和等于 1-11x- D- x+1-1a -1x+1-1 xx-11 -1 x-11 -1 k-11 -1 1 -1 1 -1 10x0 4 1x00=-) x.x.x.I=x4 1000 方法三:【思路分析】利用行列式按行(或列)展开定理降阶进行计算 1x- 1-】1x- -1 x+1-1* -1x+1-1 D= xx-11 -1 =1x-11-1 -1 -1 1 -11 1 0x- 0-e展开0- 0x0-x 00-3 000-x 【注意】降阶法是计算行列式的有效方法之一。 例1一4计算n阶行列式
线性代数学习指导 x x x x x x x x x x x x D r x r r r x r x r r r r r r 0 1 1 0 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 0 1 0 1 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 3 3 4 4 1 3 2 4 1 3 1 2 1 − − − − − = − − − − − = − − − − − = − − − − x x x x x x r r r r − − − − − − = − − − − − − − = − − 0 0 1 1 0 0 1 1 0 1 0 1 1 1 1 1 0 1 1 0 0 1 1 0 1 0 1 1 1 1 1 3 3 2 3 4 2 3 4 0 0 0 0 0 1 1 0 1 0 1 1 1 1 1 4 3 x x x x r r = − − − − − = − + 【注意】对于低阶行列式,都可直接化成三角行列式,但这样计算一般都比较麻烦, 只有对某些特殊的行列式直接化成三角行列式才有效。 方法二:【思路分析】行列式的每列元素之和等于 x 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1 1 3 1 2 − − − − − + − − − = − − − − − + − − − = + + + x x x x x x x x x x x D c c c x c c c c 2 4 4(4 1) ( 1) 1 1 0 0 0 1 0 0 1 0 0 1 0 0 4 1 3 1 2 1 x x x x x x x x x c c c c c c = = − = − + − + 方法三:【思路分析】利用行列式按行(或列)展开定理降阶进行计算 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1 1 3 1 2 − − − − − + − − − = − − − − − + − − − = + + + x x x x x x x x x x x D c c c x c c c c x x x x x c x x x x x x x x r r r r r r − − − − − − − − = − − − 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 4 1 3 1 2 1 按 展开 2 4 1 0 x x x x c x = − − 按 展开 − 【注意】降阶法是计算行列式的有效方法之一。 例 1—4 计算 n 阶行列式
线性代数学习指导 a bb. ab.b D.= b b a. b bbb.a 【思路分析】将行列式化成三角行列式 方法一:行列式的每行元素之和为a+(n-)b,则 la+(n-1)bbb.b a+(n-10bab.b D. =a+(n-l0bba.b ” . a+(n-l1bbb.a a+(n-10bbb. b 0 a-b0. 0 0 0 a-b. 0=[a+(n-1)b](a-b)- 0 0 0.a-bl 方法二:将行列式化成箭式行列式 a b b b-a a-b 0.0 D. b-a 0a-b. 0 b-a 0 0 .a-b a+(n-1)bb b . 0 a-b 0 . 0 0 0 a-b =[a+(n-1)b(a-b) 0 0 0 .a-b 【注意】形如 la1b3b.bn 0.0 D。=c30a.0 cn00.an 称为箭式行列式,它总可以通过变换℃ 。(=23川化成上三角行列式
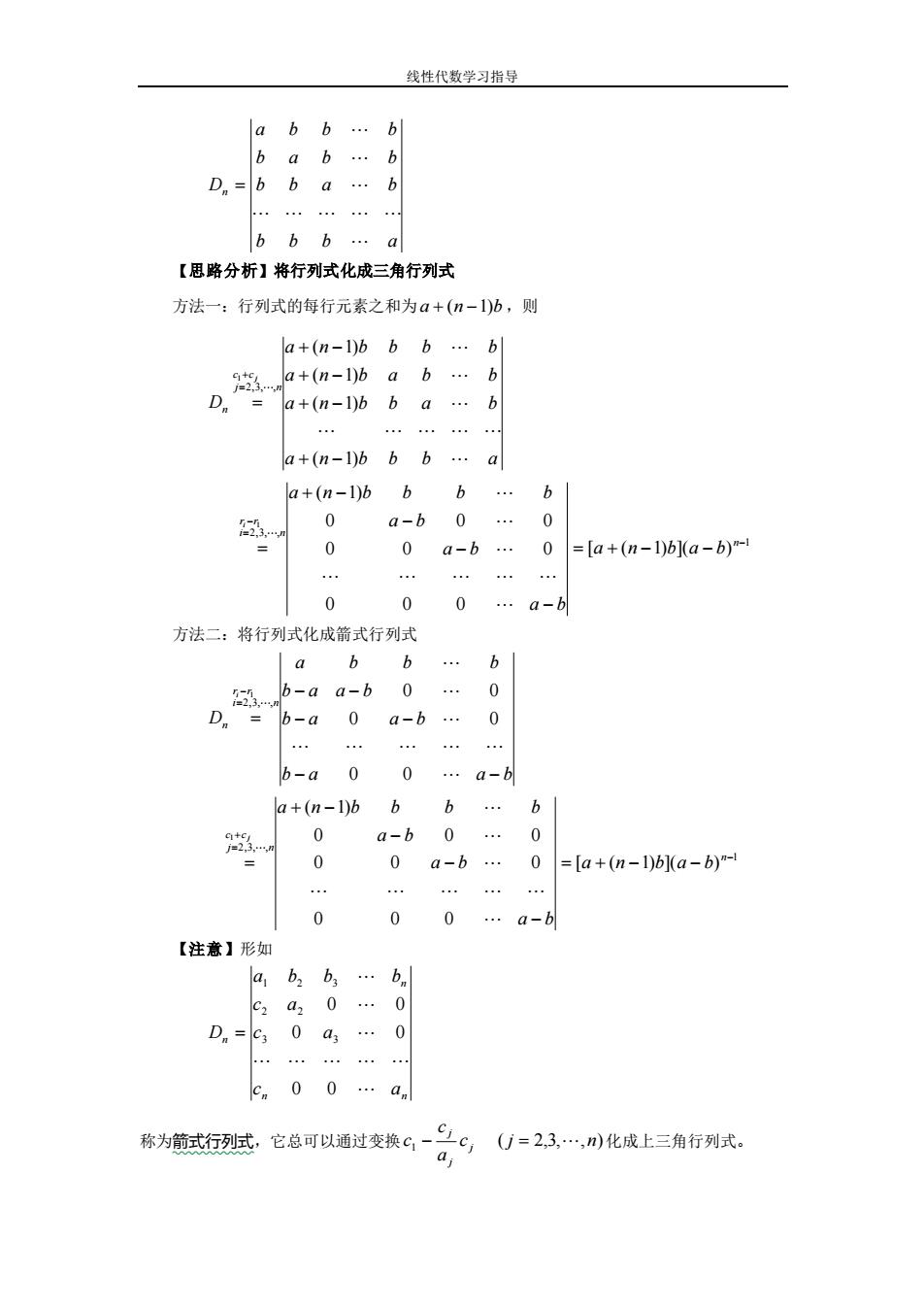
线性代数学习指导 b b b a b b a b b a b b a b b b Dn = 【思路分析】将行列式化成三角行列式 方法一:行列式的每行元素之和为 a + (n −1)b ,则 a n b b b a a n b b a b a n b a b b a n b b b b D j n c c n j ( 1) ( 1) ( 1) ( 1) 2,3, , 1 + − + − + − + − = = + 1 2,3, , [ ( 1) ]( ) 0 0 0 0 0 0 0 0 0 ( 1) 1 − = − = + − − − − − + − = n i n r r a n b a b a b a b a b a n b b b b i 方法二:将行列式化成箭式行列式 b a a b b a a b b a a b a b b b D i n r r n i − − − − − − = = − 0 0 0 0 0 0 2,3, , 1 1 2,3, , [ ( 1) ]( ) 0 0 0 0 0 0 0 0 0 ( 1) 1 − = + = + − − − − − + − = n j n c c a n b a b a b a b a b a n b b b b j 【注意】形如 n n n n c a c a c a a b b b D 0 0 0 0 0 0 3 3 2 2 1 2 3 = 称为箭式行列式,它总可以通过变换 ( 2,3, , ) 1 c j n a c c j j j − = 化成上三角行列式