
库仑定律 ·分布电荷对点电荷的作用力可以统一地表示为: )=49 -dd 4π60 JregionF p(r)dv' 体电荷 dq'=p,(r)ds' 面电荷 p,(Fdl' 线电荷 lexu@mail.xidian.edu.cn 11
库仑定律 • 分布电荷对点电荷的作用力可以统一地表示为: lexu@mail.xidian.edu.cn 11 region q dq r r q r r F r 3 0 4 线电荷 面电荷 体电荷 r dl r ds r dV dq l s

电场强度 电场强度 一两个电荷之间互不接触却能相互作用,这种作用是通过电场 进行的。 ·电场是一种特殊的物质,看不见摸不着,但可以通 过带电体的相互作用来检验它,也可以由相互作用 的强弱来度量电场的强弱。 ·用来描述电场强弱的物理量是电场强度。我们定义 位于点处的单位正电荷所受的力为该处的电场强度。 用表示,其单位为牛顿/库仑(N/C)。 一定义,在「处放置点电荷q(试探电荷),它所受的力 为F,(),则该处的电场强度为: F,) )= q lexu@mail.xidian.edu.cn 12
电场强度 • 电场强度 – 两个电荷之间互不接触却能相互作用,这种作用是通过电场 进行的。 • 电场是一种特殊的物质,看不见摸不着,但可以通 过带电体的相互作用来检验它,也可以由相互作用 的强弱来度量电场的强弱。 • 用来描述电场强弱的物理量是电场强度。我们定义 位于点处的单位正电荷所受的力为该处的电场强度。 用表示,其单位为牛顿/库仑(N/C)。 – 定义,在 处放置点电荷q(试探电荷),它所受的力 为 ,则该处的电场强度为: lexu@mail.xidian.edu.cn 12 r q F r E r q F r q
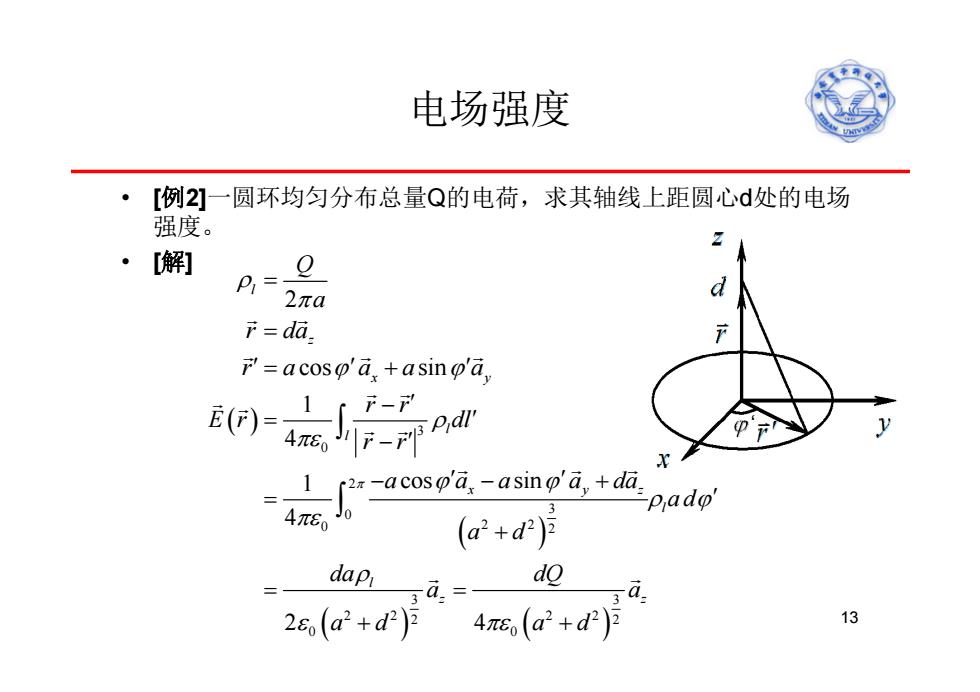
电场强度 [例2]一圆环均匀分布总量Q的电荷,求其轴线上距圆心d处的电场 强度。 解] p=0 2πa d r=da. r'=acoso'a,+asinp'a, =-o吃-aing'i.+ 4π60 pado (a2+d)月 dapi do a.= 2s,(a2+d2) 4πs(a2+d2)月 13
电场强度 • [例2]一圆环均匀分布总量Q的电荷,求其轴线上距圆心d处的电场 强度。 • [解] lexu@mail.xidian.edu.cn 13 2 cos sin l z x y Q a r da ra aa a 3 0 2 3 0 0 2 2 2 3 3 22 22 2 2 0 0 1 4 1 cos sin 4 2 4 l l x yz l l z z r r E r dl r r a a a a da a d a d da dQ a a ad ad ‘

电场强度 ·电力线 一为形象地描述电场,引入电力线的概念; - 电力线是这样的一组曲线,其上任一点处的切线方向 都与该点处的电场方向一致,电力线的密度正比于电 场强度的大小: -电力线的方程为: dx dy dz Ex Ey E 一电力线具有以下特点: ·1.起始于正电荷,终止于负电荷。 ·2.在空间无电荷区域,电力线不相交。 lexu@mail.xidian.edu.cn 14
电场强度 • 电力线 – 为形象地描述电场,引入电力线的概念; – 电力线是这样的一组曲线,其上任一点处的切线方向 都与该点处的电场方向一致,电力线的密度正比于电 场强度的大小; – 电力线的方程为: – 电力线具有以下特点: • 1.起始于正电荷,终止于负电荷。 • 2.在空间无电荷区域,电力线不相交。 lexu@mail.xidian.edu.cn 14 x y Ez dz E dy E dx

通量与散度 ·电通量 一垂直穿过某一曲面的电力线的数目称为穿过该曲面的电通量。 -在S上取一面元d§,它的投影为 ds'=ds·cos0 ·则穿过的电通量为:dw=Eds cos0=E·d5 -穿过面积S的电通量为:w=∫E·西 -若S为闭合曲面,则: w=∮E lexu@mail.xidian.edu.cn 15
通量与散度 • 电通量 – 垂直穿过某一曲面的电力线的数目称为穿过该曲面的电通量。 – 在S上取一面元 ,它的投影为 • 则穿过的电通量为: – 穿过面积S的电通量为: – 若S为闭合曲面,则: lexu@mail.xidian.edu.cn 15 ds d E ds E ds cos s E ds s E ds ds ds cos