
说明 1、必须是线弹性材料,加载在弹性范围内,服 从胡克定律。 2、必须是小变形,保证能按构件初始形状或尺 寸进行分解与叠加运算,且能保证与加载次序 无关
说明 1、必须是线弹性材料,加载在弹性范围内,服 从胡克定律。 2、必须是小变形,保证能按构件初始形状或尺 寸进行分解与叠加运算,且能保证与加载次序 无关
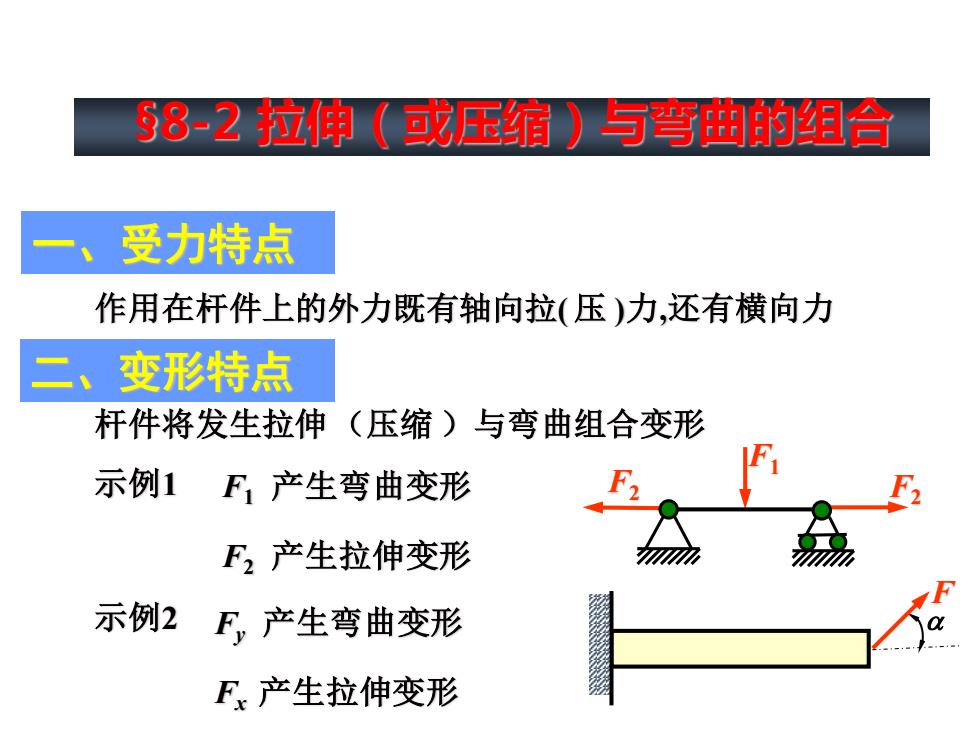
58-2拉申(或压缩)与弯曲的组合 受力特点 作用在杆件上的外力既有轴向拉(压)力,还有横向力 二、变形特点 杆件将发生拉伸(压缩)与弯曲组合变形 示例1 F,产生弯曲变形 F产生拉伸变形 示例2F,产生弯曲变形 F产生拉伸变形
作用在杆件上的外力既有轴向拉( 压 )力,还有横向力 杆件将发生拉伸(压缩 )与弯曲组合变形 示例1 F1 产生弯曲变形 F2 产生拉伸变形 示例2 Fy 产生弯曲变形 Fx 产生拉伸变形 F1 F2 F2 F §8-2 拉伸(或压缩)与弯曲的组合 一、受力特点 二、变形特点
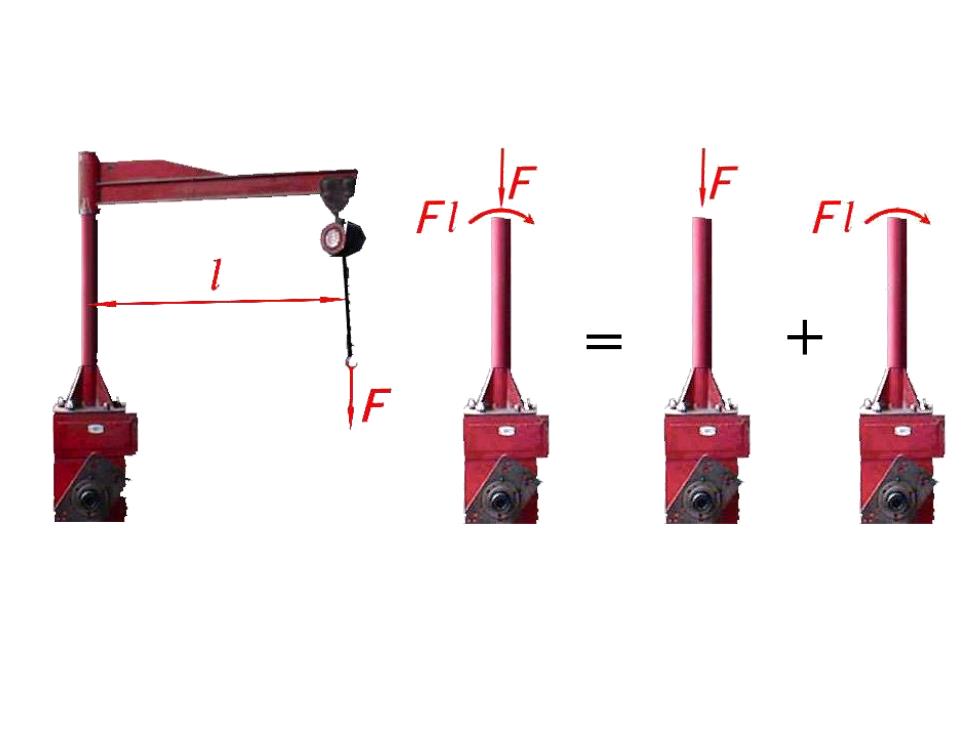
= +
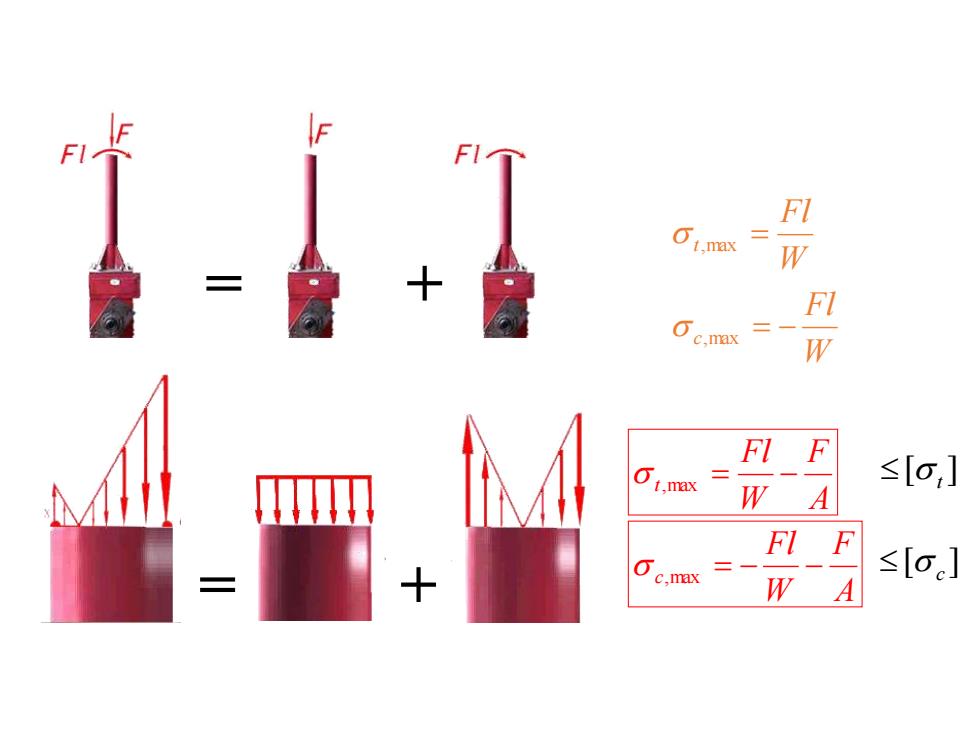
Fl 01.max W Fl Oc.max W FI F 1, ≤[o,] W A Fl F ≤[o] W A
= + = + A F W Fl t,max = − A F W Fl c,max = − − W Fl t,max = W Fl c,max = − [ ] t [ ] c
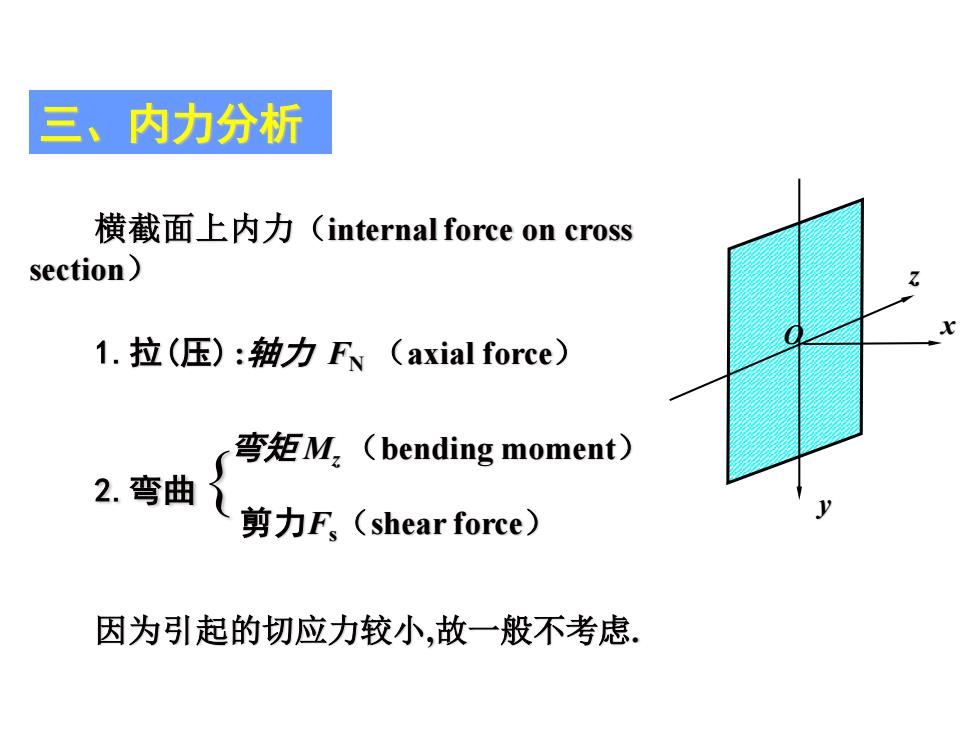
三、内力分析 横截面上内力(internal force on cross section) 1.拉(压):轴力FN(axial force) 弯矩M,(bending moment) 2.弯曲 剪力F。(shear force) 因为引起的切应力较小,故一般不考虑
三、内力分析 横截面上内力(internal force on cross section) 1.拉(压) :轴力 FN (axial force) 2.弯曲 弯矩 Mz (bending moment) 因为引起的切应力较小,故一般不考虑. x y O z 剪力Fs(shear force)