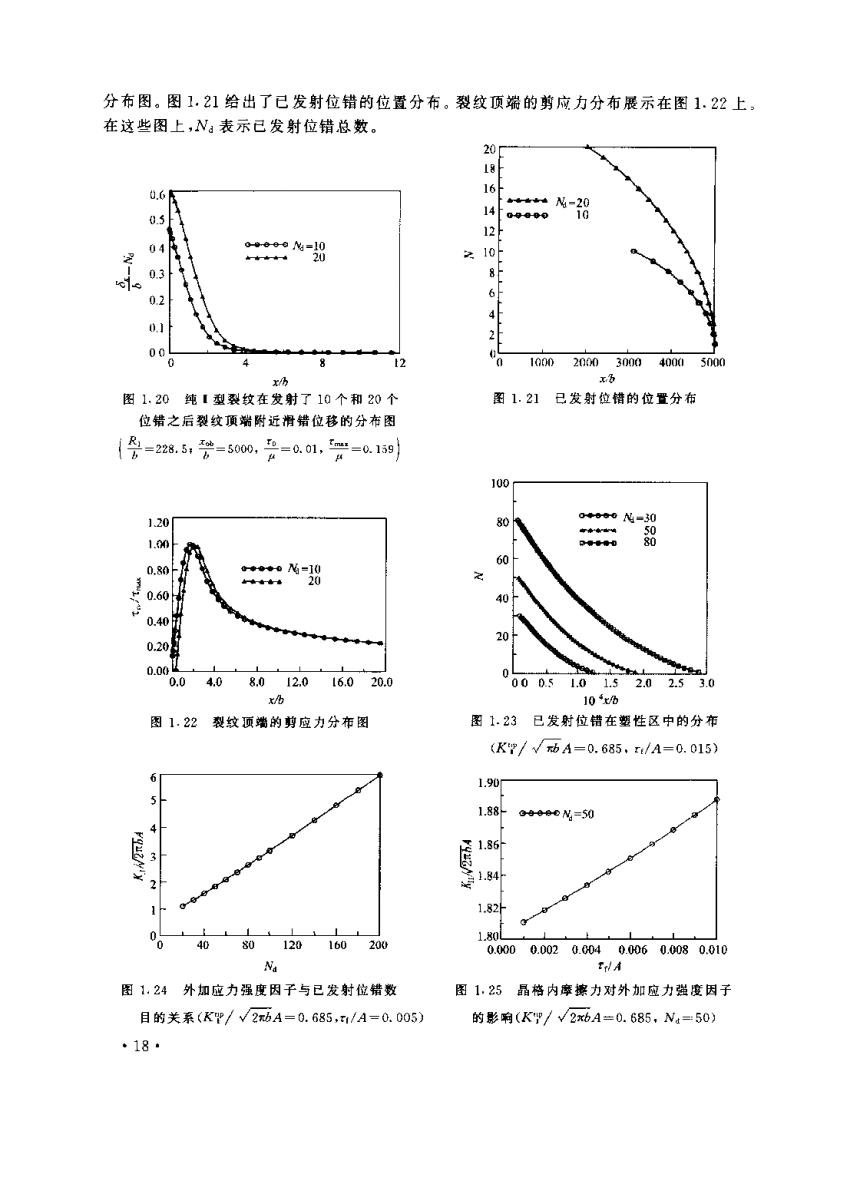
分布图。图1.21给出了已发射位错的位置分布。裂纹顶端的剪应力分布展示在图1.22上, 在这些图上,Na表示已发射位错总数。 20 0.6 16 14 0.5 6000。N-28 09g-90 12H 04 oeee=10 20 10 0.3 0.2 01 2 00 4 8 12 10002000300040005000 h xb 图1.20纯1型裂纹在发射了10个和20个 图1.21已发射位错的位置分布 位错之后裂纹顶端附近将错位移的分布图 {=2851若=500,2=0.01,g=0.159 100 1.20 80i 0603-30 1.0 peen0 60 0.80 3 %-8 0.60 40 0.40 20 0.0g 0.0 4,0 8.012.016.020.0 000.51.01.52.02.53.0 x/b 10x/b 图1.22裂纹顶端的剪应力分布图 图1.23已发射位错在塑性区中的分布 (K/√动A=0.685,r/A=0.015) 1.90 1.88 G408DM=50 d1.84 1.82 0 40 1.80 80120160200 0.0000.0020.0040.0060.0080.010 Na EA 图1,24外加应力强度因子与已发射位错数 图1,25晶格内摩擦力对外加应力強度因子 目的关系(KΨ/√2bA=0.685,x1/A=0.005) 的影响(K/V2xbA=0.685,N4=50) ·18·

利用方程(1.44)和(1.45),可以在忽略内聚力区和粘脱区影响的前提下,计算已发射位 错在塑性区中的分布。图1.23给出了一个典型算例。在这个算例中,我们设想裂纹前方不 存在障碍。从图上清楚地看出,塑性区内的位错确实以反塞积形式分布。 图1.24展现了外加应力强度因子与已发射位错总数之间的关系。而图1.25给出了晶 格摩擦力对外加应力强度因子的影响。 1.4断裂位错理论 1.4.1考虑位错发射影响的断裂准则 固体材料中裂纹脆性断裂通常伴随有相当数量的位错发射.Sinclair和Finnis[a]建议了 一个简单的考虑位错影响的断裂准则,并对纯1型裂纹进行简单的分析。他们的模型假定了 裂纹沿着原有的面扩展,排除了裂纹分叉扩展的可能性。Lin和Thomsont40]提出了复合型 受载情况下,考虑位错发射影响的断裂准则,他们的模型同样排除了裂纹分义的可能性。 根据大量的实验观察,Oh]指出,裂纹扩展是一个混合交替过程,裂纹尖端的位错发 射与裂纹解理扩展可以在同一平面内进行。这意味着裂纹尖端发射了一定数量位错之后,裂 纹沿着这些位错所在的滑移面扩展一定距离,然后第二滑移系开动,位错从新的裂纹尖端发 射一定数量后,裂纹再沿第二个滑移面扩展一段距离,如此反复,形成了“之”字形(2gzg) 扩展。 基于Ohr1门模型,王自强[建立了考虑位错发射影响的断裂准则。得到了裂纹尖端发 射一定数量位错后裂纹解理扩展的临界条件,详细分析了晶体方位几何、加载方式对临界 能量释放率的重要影响。 讨论平面应变问题。设想裂纹前缘线位于一个 分解剪应力最大的滑移面内。如图1.26所示,滑移 面与裂纹面成,角度。无穷远处承受复合型载荷 (k:十k:)。 作用在滑移面上的正应力s和剪应力可表 图1.26滑移面几何 示为 ,=号cos}k,(1+cos8,)-3次,sin。 (2πr)1A (1.46) t= 110}k,sin9。+k,(3cos0。-1) 2cos|2 (2πr)172 已发射位错所产生的应力强度因子为 b k1d= 20-2w3sin8,coe (1.47) ka=一 22.)(3com0 -1cos b。 式中b,是该刃型位错Burgers矢量的大小;r。是该位错距裂纹尖端的距离。 ·19·

引入与滑移面关联的坐标系Ox·y·,其中x·轴与滑移方向一致,y·轴与滑移面垂直。 对于Ox·y'坐标系,引入应力强度因子 K,=lim[√2rag]- (1.48) K,=lim[√2rt,e]g-。 r和0 将式(1.46)代入上式,得 K= co(2}[:1+cos9,)-k:3sin6,】 (1.49) Kcos Csind+(cos01] 类似的可以导出 Kd=一 pb. 2(1-(27.)a3sin%c0s2 【811-cos0o) (1.50) K4=一 地。 2-0(2xa)m(2+3c0s0。-3cos0)cos 裂纹尖端局部应力强度因子为 K=K+Kid (1.51) K=K+ 公式(1.51)的物理意义是很清楚的。裂纹尖端的局部应力强度因子,小于外加应力强度因 子。这种诚小是由于已发射位错的屏蔽效应造成的。 Lin和Thomson40],Rice[]建议刃型位错从裂纹顶端发射的临界条件为 Kip =Kie (1.52) 式中K是位错发射的临界应力强度因子。 依照(1.21)式, 2Y K=Ni¥ (1.53) 裂纹沿滑移面分叉扩展的准则为[们 (KP)2+(KP)2=K (1.54) 式中K是I型裂纹沿滑移面扩展的断裂韧性。 设想裂纹尖端沿滑移面发射了N个刃型位错之后,裂纹脆性扩展,扩展前裂尖局部应 力强度因子为 1 (1.55) K9-K,-2 式中,(i=1,2,…,N)是第:个已发射位错距裂纹尖端的距离。引人下列参数 (am 1 (2r:)2 (1.56) ·20·

C。= pbe 2(1-y)(2r)/2K1 (1.57) CCn() (1.58) C2=Cocos2 22+3cos8,-3c0s0,) 公式(1.55)可表示为 K=K:-NC Kie K9=Kr一NCK。J (1.59) 将上式代人(1.54)式,得 (K:-NC K)2+(K-NC2K)2=Ki (1.60) 上式可改写为 N(ci+c3)-2 VIC.ow+-C突+”=r (1.61) 式中 amp-袋,p=袋 (1.62) 如图1.27所示,当外加载荷增加时,应力强度因子K,和K,将同时沿者直线OC增加。 在A点,K,值达到K。第1个位错在裂纹尖端成核,然后沿着滑移面滑出裂纹尖端区域, 停在距离1处。此时,局部应力强度因子K和KP将从A点降至B,点,这种下降是由子第 1个已发射位错的屏蔽效应造成的。由子位错发射过程快速完成,因此,可以忽略外载在此 过程中的变化。当外载继续增加时,局部应力强度因子K和K沿着与OC平行的直线 B,A,增加。在A1点,局部应力强度因子K再次达到K1.,第2个位错在裂纹顶端成核,并 从裂纹顶端发射出来,停在距裂纹尖端2处。由子已发射位错的屏蔽作用,裂纹尖端的局部 应力强度因子减小到B,点。这样的过程反复进行,直至临界点A处,半径OAN等子K, 就会发生沿滑移面的解理扩展。 图1.27外界载荷和已发射位籍屏蔽效应 对裂端局部应力强度因子的影响 ·21-
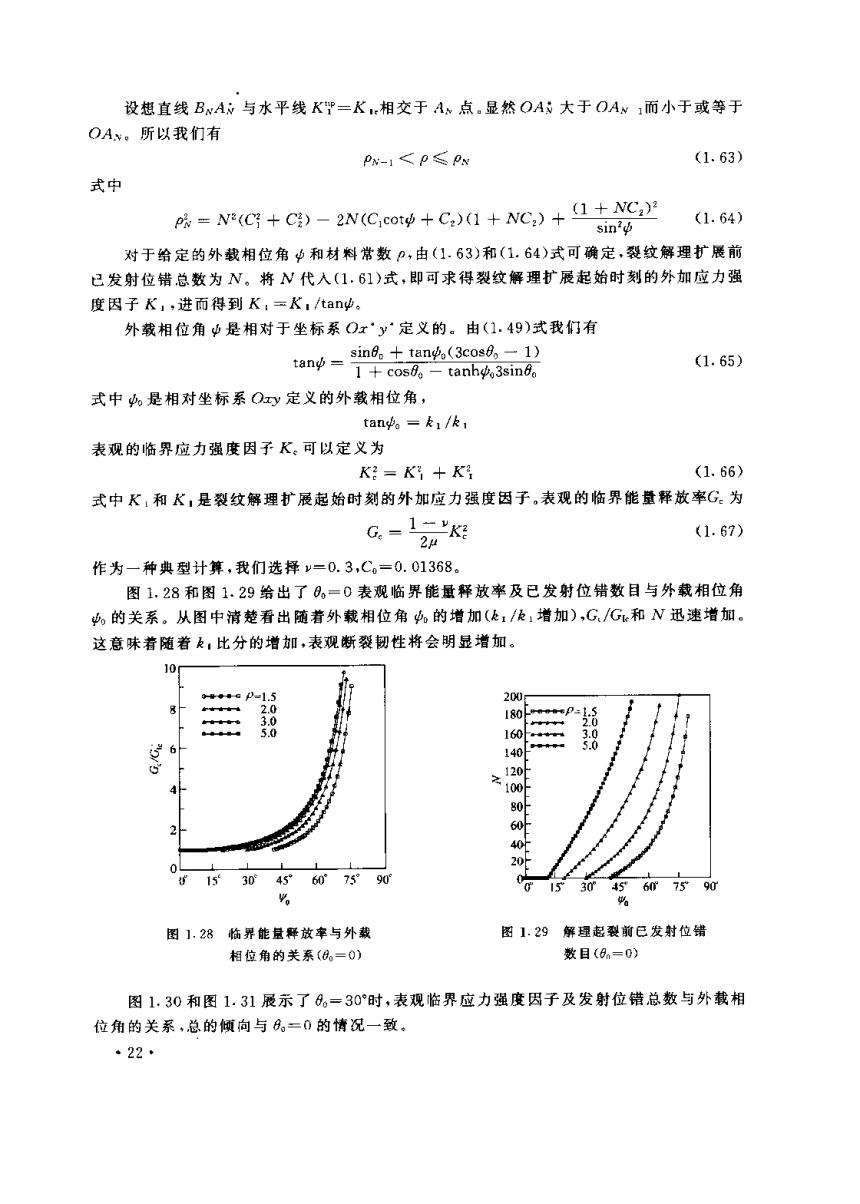
设想直线BwAN与水平线KP=K,相交于A点。显然OA大于OAw1而小于或等于 OAv。所以我们有 Px-1<p≤Px (1.63) 式中 =N(C +C])-2N(Cicot +C)(1+NC:)+(1+NC) (1.64) sin2中 对于给定的外载相位角中和材料常数P,由(1.63)和(1.64)式可确定,裂纹解理扩展前 已发射位错总数为N。将N代入(1.61)式,即可求得裂纹解理扩展起始时刻的外加应力强 度因子K,,进而得到K,=K,ftan中。 外载相位角中是相对于坐标系Ox·y定义的。由(1.49)式我们有 tand= sinf。+tan4(3cos8-1) (1.65) 1+cos8。-tanh$3sin6a 式中是相对坐标系Oy定义的外载相位角, tan中。=k1/k1 表观的临界应力强度因子K。可以定义为 K:=K+ (1.66) 式中K:和K,是裂纹解理扩展起始时刻的外加应力强度因子,表观的临界能量释放率G。为 G=12#K (1.67) 作为一种典型计算,我们选择y=0.3,Co=0.01368。 图1.28和图1.29给出了0,=0表观临界能量释放率及已发射位错数目与外裁相位角 的关系。从图中清楚看出随着外载相位角的增加(k1/k:增加),G/G和N迅速增加。 这意味着随着,比分的增加,表观断裂韧性将会明显增加。 10 200 2.0 180 Lweewep-1.5 3.0 2.0 5.0 160 3.0 6 140 5.0 5 ÷120 100 80L 60 40以 0 153045°60°75°90 304567590 % % 图1.28临界能量释放率与外载 图1.29解理起裂前已发射位错 相位角的关系(8。=0) 数目(8=0) 图1.30和图1.31展示了0。=30°时,表观临界应力强度因子及发射位错总数与外载相 位角的关系,总的倾向与6。=0的情况一致。 ·22*