
d8(p) (1.22) V2xF 式中第二项积分核表征了处于,=p处的刀型位错_dPap在r处所产生的剪应力及 其与裂纹面交互作用的象力之和。由于裂纹前方内聚力区中连续分布位错将对裂纹产生完 全的屏蔽效应,因此,裂纹顶端的应力奇异性应该消失。所以 &,=31-元2dp (1.23) 将上式代入(1.22)式得 d8(p) x(r)=- (1.24) 该剪应力应该与内聚力相等, d8(p) ro)=0m答9=-22-V后oe (1.25) 方程(1.25)即是关于6(r)的定解方程。该方程的求解方法将在后面讨论。 对于复合型受载的情况,Bltz和Rice[a]给出了类似的分析,发现I型外载的存在将会 略微降低位错发射所需要的临界应力强度因子K,值。 1.3.3位错发射理论分析 Riceis],Schoeck[],Rice等人[a门和Betz和Rice[s]对位错在裂纹顶端的成核过程作了 详尽的分析。但是他们的分析方法难以推广到分析裂纹顶端位错发射过程。 王自强[36]对RiCe[33)提出的模型作了修正,成功地对裂纹尖端位错成核及位错发射过程 进行了力学分析。设想滑移面两侧晶体的滑错只在分解剪应力充分大时才能发生。此时,公 式(1.16)变为 T≤To (1.26) 8,+th,r 式中。是理想晶体产生滑错所需的临界剪应力;6,是滑移面两侧相对滑错。类似的,用6, 表示滑移面两侧法向位移间断,△,表示滑移面两侧的两个相邻原子面之间法向相对位移, 则有 E 0,≤d0 ,= (1.27) ®+2,马,> 式中。是理想晶体滑移面的两侧产生法向位移间断所器要的临界正应力。 对于一般正应力与剪应力共同作用的情况,我们采用如下的内聚力公式[): ·13
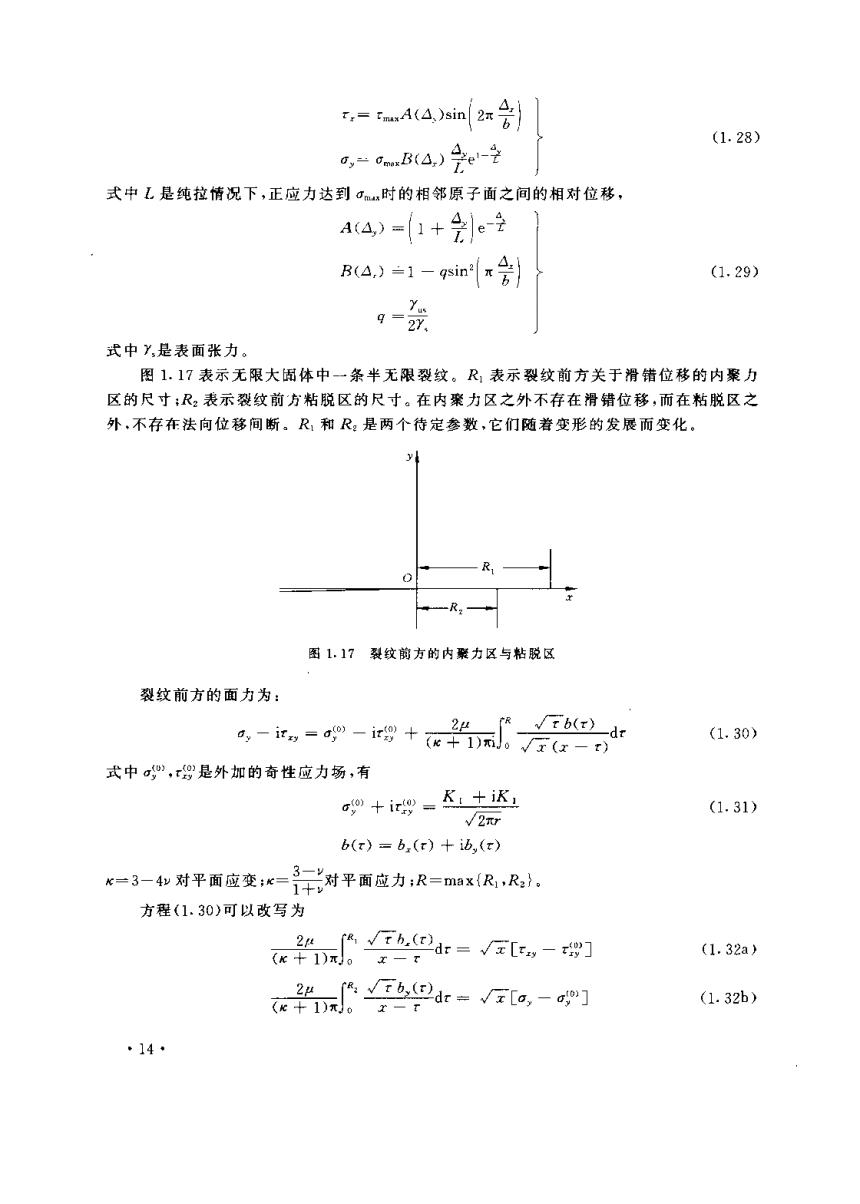
,=A4sin2x÷ (1.28) 0y=0xB(△) 式中L是纯拉情况下,正应力达到a,时的相邻原子面之间的相对位移, A4)=1+e受 B(4,)=1- in】 (1.29) g=2Y. 式中Y,是表面张力。 图1.17表示无限大固体中一条半无限裂纹。R表示裂纹前方关于滑错位移的内聚力 区的尺寸:R:表示裂纹前方粘脱区的尺寸。在内聚力区之外不存在滑错位移,而在粘脱区之 外,不存在法向位移间断。R和R:是两个待定参数,它们随着变形的发展而变化。 R: 图1.17裂纹前方的内聚力区与粘脱区 裂纹前方的面力为: ,-,=-喝+0 (1.30) 式中a,9是外加的奇性应力场,有 af+ir= K+iK (1.31) √/2r b(r)=b(r)+b,(x) 6=3一4和对平面应变:k=十对平面应力:R=DaxR,R. 方程(1.30》可以改写为 2rR√Fh.dr=√x[c,-母] (K+1)π。x-x (1.32a) 2F6,dr=√x[a,-g] (e+1)元J。x-r (1.32b) ·14·

式中x,0,等于公式(1.28)表示的内聚力x,0,。方程(1.32)是复杂的非线性积分方程。 为了有效而精确地求解方程(1.32),王自强61提出了新的分析方法。引人新的自变量 0,9 辰=1+cos0),0≤0≤x (1.33) 元-21+c0s,0≤e≤x 采用以下正弦级数展开, (1.34) xfD√危,)= 则不难证实 m,=冬.@ (1.35) +D,-》a.v.(p V(8)= sm[m-29]_s加[m+20] (1.36) m一之 m十立 √,-)=】 o(m) (1.37) √元a,-9)=∑A.co8(m r 将式(1.28)代人式(1.37),就得到关于系数{an},{Pn}的非线性函数方程。在内聚力区及粘 脱区内适当选择配置点,让(1.37)式在这些配置点上得以满足,就得到关于系数{am,m=1, 2,,M},{Bnm,m=1,2,…,N}的非线性代数方程组。利用Newton-Raphson方法求解,即可 得到有效而精确的解答。 图1.18显示了纯Ⅱ型裂纹,裂纹前方的滑错位移在不同外载水平下的分布图。当能量 释放率G等于不稳定堆垛能Y时,一个完全的刃型位错已在裂纹尖端成核。从图1.19可以 清楚地看出刃型位错的发射过程。当R1/b=302.5时,已发射的刃型位错已经距离裂纹顶端 约x一5.4b.从该图还可以清楚地看到,在裂纹顶端与已发射位错之间可以存在一个滑移面 上下晶体滑错一个晶格常数b而后重新理想结合的区域。这个区域也就是众所周知的无位 错区。 当已发射位错滑出裂纹顶端区域,就可能塞积在远离裂纹顶端的塑性区内,而在裂纹顶 端与塑性区之间出现无位错区。 王自强等人〔3门[3)建立了裂端位错成核、位错发射及无位错区的统一模型。塑性区中的 已发射位错看作是离散的弹性刃型位错。裂纹顶端附近的内聚力区和粘脱区处理成连续分 ·15·

0.6 0.4 G%.=l.0004 0.2 0.9 0.7 0.5 0.0 0.0 1.0 2.0 3.04.05.06.07.0 b 图1.18纯1型裂纹,滑错位移分布图 125 1.00 0.75 是 0.50 Rb=362.51 302.5 0.25 262.5 0.00 0.0 5.0 10.015.0 20.0 25.0 6 图1.19刃型位错发射过程 布的位错。 裂纹前方应力场可表示为 -i,=o9-g+ f (()+ib,(r)dr √x(x-r) 2pib V ++1)mi台√x(x) (1.38) 式中n是已发射位错数目:x4(k=1,2,…,n,x>x+i)是已发射位错在塑性区内的位置,区 间[R,x]是无位错区。 采用(1.34)式的展开式,不难导得 ·16·

e中=是2.v0+年0,0≤x≤R (1.39) 06≤x≤R: n-N2a.ws-e6a》+ 2地 I K十1)π台 x≤R1 √x4(x-x) e,-√∑A.os6m9-cosa x≤R2 (1.40) 作用在塑性区内第)个离散位错上的剪应力为 (1.41) 式中 T.()=[7-√-1]” =2是-1 作用在每个离散位错上的剪应力应该等于晶格的摩擦力, ty=4j=1,2,…,n (1.42) (1.42)式给出了n个补充方程。这样我们就有了足够的方程来确定未知量{am},{9}及 xa 如果第1个已发射位错受阻于障碍物x处,那我们有约束方程 TI=To (1.43) 如果我们忽略裂纹顶端的内聚力区和粘脱区,我们可以得到 + (1.44) √2xz 2x4 式中A0=2/(x十1)π。 裂纹顶端的应力强度因子K为 灯-属会语 (1.45) 图1.20~图1.22给出了若干典型结果,计算中材料参数取为 各=1,台=0.4,=0.3, 是=0.05,2=0.01,分=0.159 阳1.20显示了纯1型裂纹在发射了10个和20个位错之后,裂纹顶端附近滑错位移的 ·17·