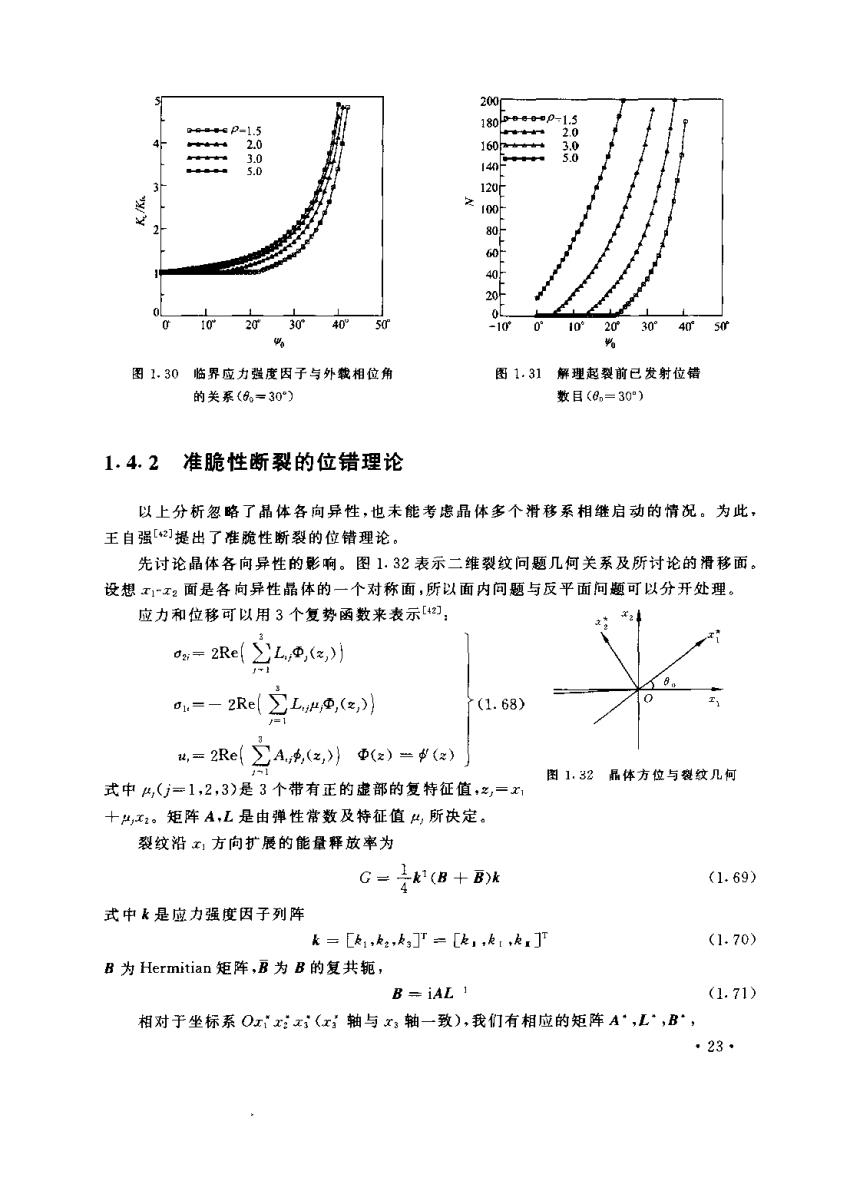
200 60P-1.5 096P-1.5 180 2.0 2.0 160 3.0 3.0 5.0 5.D 100 80h 40 2 0 10 2030°40°50 -100° 10°2030°4050m 年 图1.30临界应力强度因子与外载相位角 图1.31解理起裂前已发射位错 的关系(8。=30) 数目(0,=30°) 1.4.2准脆性断裂的位错理论 以上分析忽略了晶体各向异性,也未能考虑晶体多个滑移系相继启动的情况。为此, 王自强[2]提出了准跪性断裂的位错理论。 先讨论晶体各向异性的影响。图1.32表示二维裂纹问题几何关系及所讨论的滑移面。 设想x1~x2面是各向异性晶体的一个对称面,所以面内问题与反平面问题可以分开处理。 应力和位移可以用3个复势函数来表示[42幻: s=2Re(L,(,) a=-2Re(L®,(e, (1.68) u,=2Re(∑A4,(z,} (z)=(x) 图1.32品体方位与裂纹几何 式中4,(=1,2,3)是3个带有正的虚部的复特征值,之,=x1 十H,x2。矩阵A,L是由弹性常数及特征值4,所决定。 裂纹沿x1方向扩展的能量释放率为 G=⊥k1(B+B)k (1.69) 式中k是应力强度因子列阵 k=[k1,k,k3]r=[k,,k:,k] (1.70) B为Hermitian矩阵,B为B的复共轭, B=iAL (1.71) 相对于坐标系Ox”x:x(x轴与xa轴一致),我们有相应的矩阵A·,L·,B·, ·23·

A·=RA,L·=RL,B"=RBRT (1.72) 式中R是坐标变换矩阵 cos6o sind.0 R -sin0。cos0.0 (1.73) 0 01 相对于坐标系Ox1x2x,有应力强度因子 K=[K1,K2K3=[K,K:,KT (1.74) K=fk (1.75) 实矩阵∫的表达式见文献[42]。 位于点(x,y)的刃型位错与半无限裂纹的交互作用,其对应的复势函数可表示为 z十2 (1.76) 式中,=xu十4yo,列向量d及矩阵C为 d=b (1.77) C=LL 式中b是刃型位错的Burgers矢量。 该刃型位错所产生的应力强度因子为 K=-4 (1.78) √2πr0 q.的具体式子见文献[42]。 裂纹顶端的局部应力强度因子为 Ki=K,+K3 (1.79) 刃型位错在裂纹顶端成核后从裂端发射的临界条件为 K-Ki (1.80) 对于各向异性材料,我们有3? -2 (1.81) 式中山n是有效剪切模量;是有效Poisson系数。 裂纹沿滑移面分枝扩展的临界条件为 a11(K)2+2a1zK+a2(K)2=Gc (1.82) 式中a=(B·十B·),/4 设想在N个刀型位错从裂纹顶端发射后,局部应力强度因子为 N 11 K=K,-g}2(2严 (1.83) 式中r,(i=1,2,…,N)是第i个刃型位错距裂纹顶端的距离。引人下述参数 ·24·

1 9, (51152)1/g c1*(2nK.=9 (1.84) b b 9o=(2xr)0R.(5152)a 公式(1.83)变为 KiP Ki-NciKi (1.85) 将(1.85)式代入(1.82)式,得 a11(K,-NKc1)2+2a1(K1-NK1c1)(K&-NKc)+a22(K2-NK1c2)2=Gk (1.86) 该方程可以转化为 .-2b.np (1.87) 式中 a。=dutan2中+2a12tany+a22 bo=ancitang +an2(c+citand)+azzc2 (1.88) co=aci十2a1:c3c2+a2c a==炎 (1.89) Kie px二Ke (1.90) Px是断袋韧性K与刃型位错从裂纹顶端发射的临界应力强度因子K的比值:中是相对于 坐标Oxx2x的外载相位角。 图1.33表示了外加载荷和已发射位错的 屏蔽效应对局部应力强度因子的影响。 采用1.4,1节中的分析方法,不难求得裂 纹沿滑移面解理扩展的表观临界应力强度因 子,及扩展起始时刻的已发射位错总数N。 1.正交各向异性体 对于正交各向异性体,平面问题包含4个 弹性常数:51,52,51z和56。引入两个无量纲参数 2s12十566 0.3 1.0 1.5 2.0 d=,p=2a7元 (1.91) K 参数入表征x1方向与x:方向杨氏模量各向异 图1.33外载及已发射位错对裂端局 性:P表征x1-x?平面剪切模量各向异性。 部应力强度因子的影响 特征方程和特征值为 r+2P/r2+1=0 (1.92) ·25·
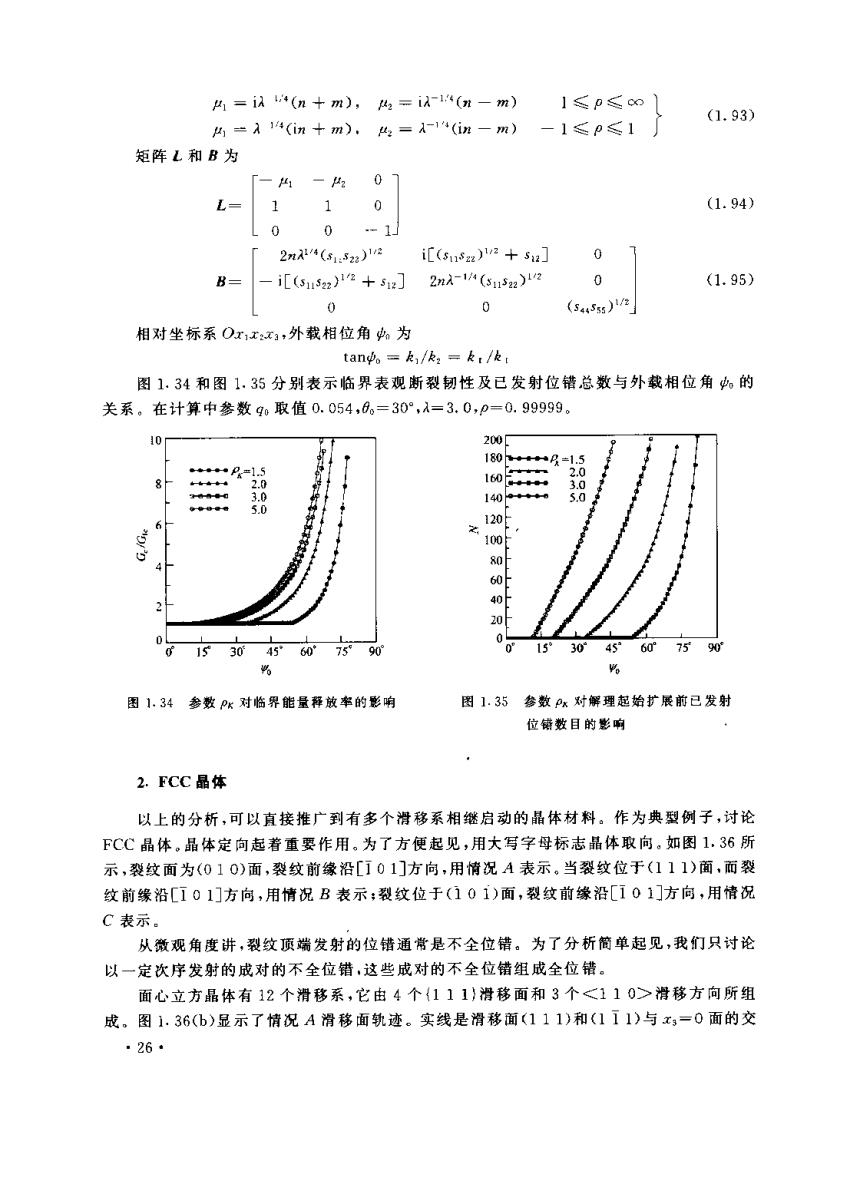
41=i24(n十m),42=i以1(n-m) 1≤po (1.93) 以1=A14(in+m),42=A14(in-m) -1≤p≤1 矩阵L和B为 一41 07 L= 1 0 (1.94) 0 -1」 2n4(s132)1a i〔(511sz)2+5z] 0 i[(51152)2+51z] 2n入1(s152)12 0 (1.95) 0 (s455)1e 相对坐标系Ox1xxa,外载相位角为 tan中。=k1/k2=k,/k: 图1.34和图1.35分别表示临界表观断裂韧性及已发射位错总数与外载相位角的 关系。在计算中参数q6取值0.054,。=30°,A=3.0,p=0.99999。 10 200[ 180A〧1.5 ★★ 2.0 160 2.0 0。-●- 3.0 3.0 140 5.0 5.0 120 100 80 60 40 20 0153045°60°7590 0°15°30°45607590 % % 图1,34参数P5对临界能量释放率的影响 图1.35参数Px对解理起始扩展前已发射 位错数目的影响 2.FCC晶体 以上的分析,可以直接推广到有多个滑移系相继启动的晶体材料。作为典型例子,讨论 FCC晶体。晶体定向起着重要作用。为了方便起见,用大写字母标志晶体取向。如图1.36所 示,裂纹面为(010)面,裂纹前缘沿[101]方向,用情况A表示。当裂纹位于(111)面,而裂 纹前缘沿[工01]方向,用情况B表示:裂纹位于(101)面,裂纹前缘沿[101]方向,用情况 C表示。 从微观角度讲,裂纹顶端发射的位错通常是不全位错。为了分析简单起见,我们只讨论 以一定次序发射的成对的不全位错,这些成对的不全位错组成全位错。 面心立方晶体有12个滑移系,它由4个111}滑移面和3个<110>滑移方向所组 成。图1.36(b)显示了情况A滑移面轨迹。实线是滑移面(111)和(111)与x3-0面的交 ·26·

线。滑移系[110](111)和[011](111)的同时等量滑移相当于等效滑移系[121](111) 上滑移。该等牧滑移系的滑移方向平行于滑移面(111)与x=0面的交线。类似的我们有 第2个等效滑移系[121](111)。对于面心立方晶体,(010)面是-个解理面面不是滑移 面(对平面应变问题),因此,[101](010)不是一个可以接受的滑移系。对于平面应变问 题,只有2个等效滑移系。如果将反向滑移看作是另一个滑移系,那么我们总共有4个等效 滑移系,6个解理扩展方向。 00] x2010]0 (111 ✉01] 1011 (1) x101] (Π1) (a) (b) 图1.36面心立方品体滑移系及其在平面应变问题中的等效滑移系 为了方便起见,每个等效滑移系用-个数M(=1,2,4,5)表示。裂纹在解理面(010) 上,沿[101]方向及[101]方向扩展分别用M=3和M=6表示。当然,每个滑移系也可看 作是可能的裂纹扩展方向。图1.37(a)显示了等效滑移系。 (b 图1.37等效浙移系及坐标系的转换 对于面心立方晶体,晶体主轴分别是x,y,x方向。对于这个晶轴坐标系,晶体具有立方 对称性。从坐标系Oxyz转向坐标系Ox1x2x:的转换矩阵为R coss 0 sin 010 (1.96) L-sing0cos」 式中=45°。 用o。和e表示坐标系Oxyz中的应力列阵和应变列阵,面。和。表示坐标系Ox1x2x3 中的应力列阵与应变列阵 ·27·