
将裂纹尖端进一步放大,就能获得加载后裂尖A附近晶格变形情祝。如图1.12所示, 裂尖附近的晶格严重扭曲,完整晶格六角点阵的排列方式遭到破坏。图1.12中E,F,G区域 的尺寸约11m,裂尖前方存在许多空位聚合体。而E,F,G区域之外,晶格畸变不是很大,基 本上保持了周期性排列。 图1.12加载裂纹尖端原子尺度的AFM像 1.3裂端位错发射理论分析 1.3.1早期Rice-Thomson理论 Rice和Thomsonte)于1974年最先提出了裂纹尖端发射位错理论。设想一个螺型位错 沿着与裂纹面共面的滑移面,从裂纹尖端发射出来,如图1.13所示。驱动这个螺型位错沿 x轴方向滑移的剪应力为 =KI (1.1) √2πx4πx 式中x是位错离开裂纹尖端的距离:K,是外加的应力强度因子;4是剪切模最;b是Burgers 矢量的大小。(1.1)式右端的第一项是外加截荷在裂纹尖端产生的奇性应力场:第二项则是 位错与裂纹面交互作用产生的象力。对于半无限裂纹,此公式给出的象力是严格正确的。 作用在位错上的驱动力必与晶格的摩擦力,相平衡,由此得到 √/2πx 4花=石 (1.2) 方程(1.2)有两个根,它们分别是x。及x: √E-K,-√K-2如 (1.3) 2/2πx √F=K,+VK-2br (1.4) 2/2rx ·8

对于给定的材料,4,b,均是材料常数。从公式(1.3)和(1.4)看出,xn随着K:的增加而减 小,而x1随着K,的增加而增加。 夜拉应力(是 总应力 1型裂纹 象应力() 与裂纹尖端 的距离 图1,131型裂纹顶端附近作用在位错.上的剪应力x 反之,K,随着x1的增加而增加。Rice和Thomson6认为,裂纹尖端存在着一个位错 芯,其半径为r。只有当位错距裂纹尖端的距离x1超过,才可能从裂纹尖端发射出来。因 此,他们提出如下位错发射准则: K,≥h+V2 (1.5) 2V2πr. 滋 K.=地+√2m (1.6) 2V2πr 则(1.5)式变为 K,≥K (1.7) 式中K是螺型位错沿着与裂纹面共面的滑移面从裂尖发射的临界应力强度因子。它依赖 于剪切模量,Burgers矢量的大小、晶格的摩擦力及位错芯半径。 类似的分析给出刃型位错沿着与裂纹面共面的滑移面从裂尖发射的条件为 K:≥Ka (1.8) 式中 K ie= ub =+W2πr:t (1.9) 2(1-)√2rr: 对于】型裂纹,情况比较复杂,此时,刃型位错将沿着两个对称分布的倾斜滑移面从裂 尖滑出。成对发射的刃型位错彼此间有交互作用。作用在位于上半平面的刃型位错上的驱 动力为 tn s nos号-4他r-22,2 (1.10) 2√2πr 式中Y是表面能:8为滑移面与裂纹面之间的夹角;B=re32/2。式中右端第一项是外加K, 场所产生的剪应力,第二项是象力,第三项是裂纹火端钝化所产生的剪应力。式(1.10)是 ·9·
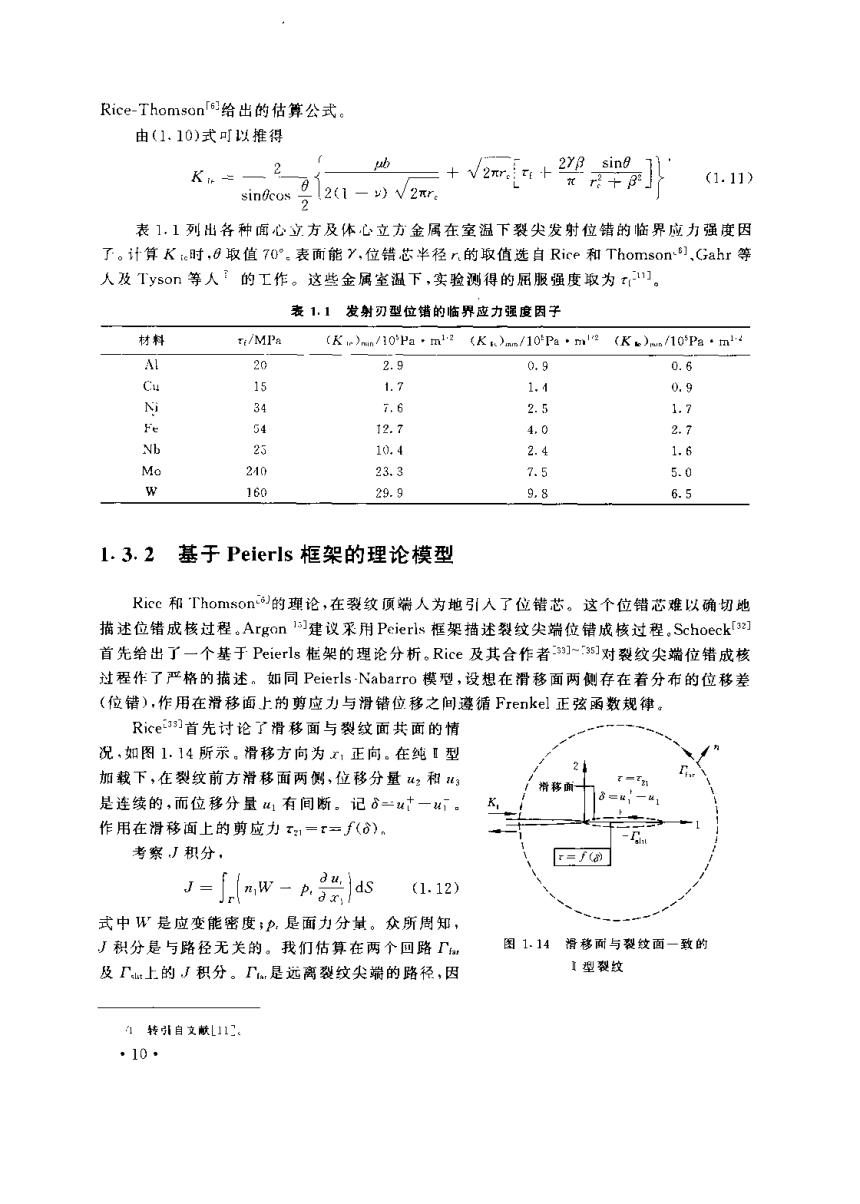
Rice-Thomson6给出的估算公式e 由(1.10)式可以推得 278 sin K一 s012(1-)√2r: (1.11) sindcos 2 表1,1列出各种面心立方及体心立方金属在室温下裂尖发射位错的临界应力强度因 了。计算Kre时,0取值70°.表而能Y,位错芯半径r.的取值选自Rice和Thomson].Gahr等 人及Tyson等人?的工作。这些金属室温下,实验测得的屈服强度取为t1门。 表1.1发射刃型位错的临界应力强度因子 材料 ri/MPa (Kr)mn/i0Pa·m2(K)mn/10Pa·nn2 (Ke)nf10Pa·md Al 20 2.9 0.9 0.6 Cu 15 1.7 1.4 0.9 i 34 7,6 2.5 1.7 Fe 54 12.7 4.0 2.7 Nb 25 10.4 2.4 1.6 Mo 210 23.3 7.5 5.0 w 160 29.9 9.8 6.5 1.3.2基于Peierls框架的理论模型 Ricc和Thomson的理论,在裂纹顶端人为地引人了位错芯。这个位错芯难以确切地 描述位错成核过程。Argon1建议采用Peierls框架描述裂纹尖端位错成核过程.Schoeck「3] 首先给出了一个基于Peierls框架的理论分析。Rice及其合作者]-3们对裂纹尖端位错成核 过程作了严格的描述。如同Peierls-Nabarro模型,设想在滑移面两侧存在着分布的位移差 (位错),作用在滑移面上的剪应力与滑错位移之间遵循Frenke】正弦函数规律。 Rice3]首先讨论了滑移面与裂纹面共面的情 况,如图1.14所示。滑移方向为x1正向。在纯Ⅱ型 加载下,在裂纹前方滑移面两侧,位移分量2和 滑移而 是连续的,而位移分量山1有间断。记6二十一。 作用在滑移面上的剪应力x,=x=f(ò)。 考察J积分, r=f(剂 du.ds Jmw-p. (1.12) 式中W是应变能密度;P,是面力分量。众所周知, J积分是与路径无关的。我们估算在两个回路T 图1.14滑移而与裂纹面一致的 及T:上的J积分。T是远离裂纹尖端的路径,因 1型裂纹 1转引自文献L1门。 ·10·

此,在回路Γ,上的J积分只依赖于K,,我们有 1=G=1-)K (1.13) 2 另一方面,在回路Γt上,J积分为 J=-02-9d,=-r2,=6=) (1.14) 式中dp是裂纹尖端的滑错位移;乎是内聚力势。在T及T上算得的J积分必须相等,由 此得到 G=1-K=Φ(6,) (1.15) 2 现在来分析内聚力。两个相邻的滑移面之间的相对位移△,是由它们之间弹性剪切所产 生的相对位移及这两个面之间的相对滑错6所组成 4=8+4 (1.16) 式中h是两个相邻滑移面之间的间距:π是作用在滑移面上的分解剪应力。?与△之间的关 系可用Frenkel正弦函数表示 t= -sin(2r△/b) (1.17) 2πh 引入势函数乎(△),P(6) dΨ=rdAl (1.18y dΦ=rd8 由此不难推得 dg=dΦ+bdr (1.19) 利用(1.17)式,导得 平= i会 b (1.20) Φ= in会 由此看出当4二名时,中与业同时达到最大值义。三是一个新的固体物理参数,称之 为不稳定堆垛能。图1,15表示了势函数中与滑错位移8的关系曲线。为了理解x与8之间 的关系,讨论简单立方晶体剪切。如图1.16所示,晶格点阵图1.16(a)~(d)分别对应着x△ 关系曲线上的a一d点。所有这些图像都表明滑移面上下两块晶体的均匀剪切变形。但剪应 力比较大时,滑移面两测发生明显的滑错。位置d对应着剪应力为零的不稳定平衡状态。此 时滑移面上下两侧晶体相对滑错了b/2。这是-一种不稳定堆垛构形,造成这种构形所需的能 量为Ys。 显然当G超过Y时,不存在任何平衡解容。瞬时的位错构形丧失稳定的临界条件为 G=12w"K= (1.21) 。11·
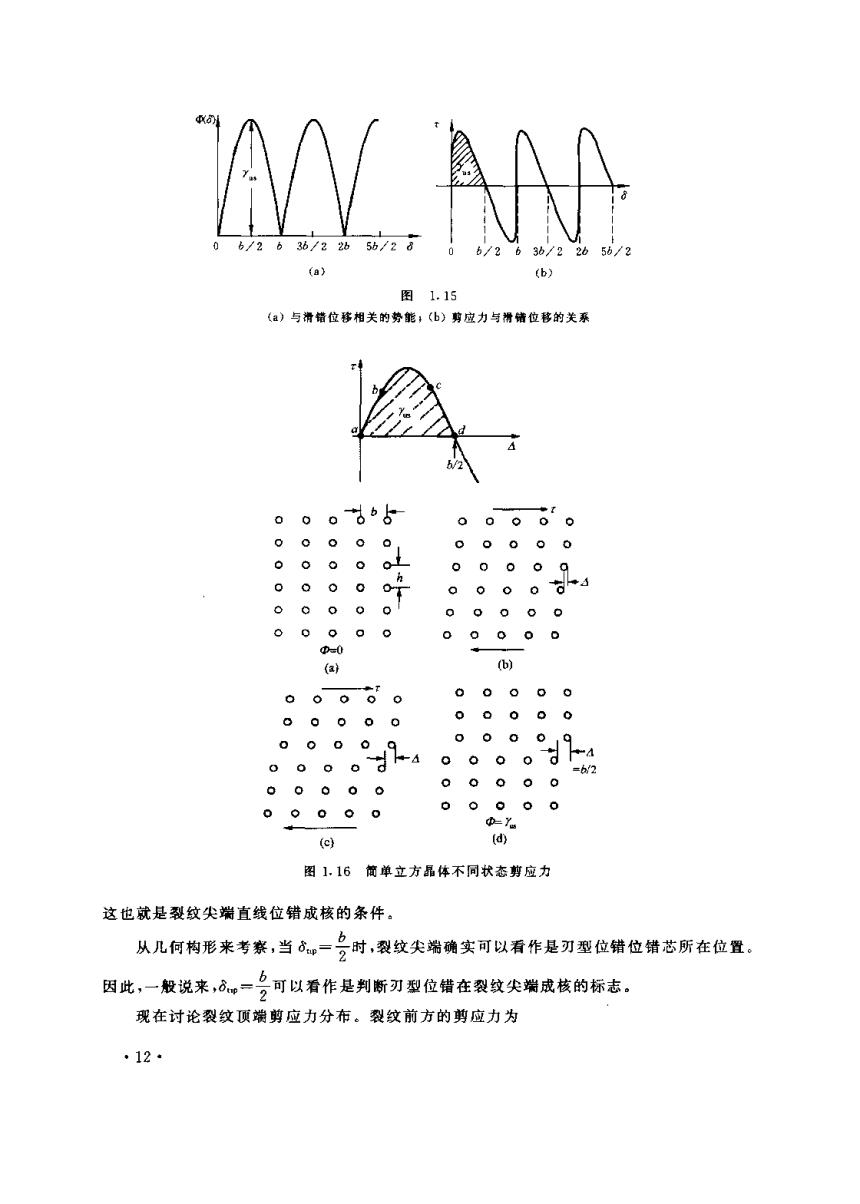
0b/2b3b/22b5b/28 6/263b/22b (a) (b) 图1.15 ()与滑错位移相关的势能;(b)剪应力与滑错位移的关系 0 0 00.0 0 00 0 000 0 h 9 00 00 08d 0 0000 0 000 0 00 000 p=0 (a) (b) T 0.0 0 0 00 0 00 000 0 00 019 000od 0 0 0 =62 0000 0 0 00 0 0.0.0 -Ya (c) d 图】.16简单立方晶体不同状态剪应力 这也就是裂纹尖端直线位错成核的条件。 从儿何构形来考察,当心,一台时,裂纹尖端确实可以看作是刃型位错位错芯所在位置。 因此,一般说来,心,一号可以看作是判新刃型位错在裂纹尖测成核的标志。 现在讨论裂纹顶端剪应力分布。裂纹前方的剪应力为 ·12-