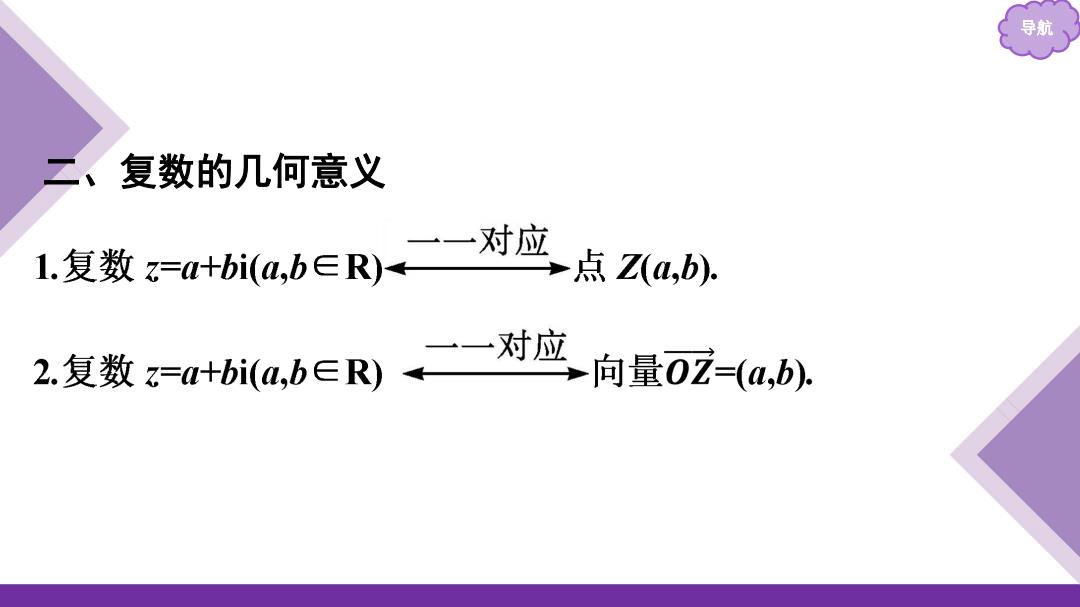
导航 二、复数的几何意义 1.复数=u+bia,b∈R)一对应 点Za,b) 2.复数&+bi(a,b∈R)-对 向量0i-(a,b)
导航 二、复数的几何意义

导航 三、复数的运算 1复数的加、减、乘、除运算法则 设z1=+biz2=c+di(a,b,C,d∈R),则 (1)加法:z1+z2=(a+bi)+(c+)= (2)减法:z1-z2=(a+bi-(c+)= (3)乘法:z12=(a+bi)(c+= 4除法子= a+bi (a+bi)(c-di) Z2 (c+di)(c-di)
导航 三、复数的运算 1.复数的加、减、乘、除运算法则 设z1=a+bi,z2=c+di(a,b,c,d∈R),则 (1)加法:z1+z2=(a+bi)+(c+di)= (a+c)+(b+d)I ; (2)减法:z1-z2=(a+bi)-(c+di)= (a-c)+(b-d)I ; (3)乘法:z1z2=(a+bi)(c+di)= (ac-bd)+(ad+bc)I ;

导航 2.做一做: ()复数(3-2i)的实部是 ,虚部是 (2)若复数a-3i与(1-bi)2互为共轭复数,则实数= ,b= 3)若复数是纯虚数,则实数m
导航 2.做一做: (1)复数(3-2i)i的实部是 ,虚部是 . (2)若复数a-3i与(1-bi)i2互为共轭复数,则实数a= ,b=

导航 解析:(1)3-21)=2+3i,则实部是2,虚部是3. (2)(1-bi1i2=-1+bi,则a=-1,b=3. m-i 3 (m-i(3-4i)= (3m-4)-(3+4m)i 3+4i (3+4i)(3-4i) 25 根据题意知,3m-4=0,且-(3+4m≠0, 4 所以m 答案123(2-13(3
导航 解析:(1)(3-2i)i=2+3i,则实部是2,虚部是3. (2)(1-bi)i2= -1+bi,则a=-1,b=3. 根据题意知,3m-4=0,且-(3+4m)≠0

【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“义” (1)方程x2+x+5=0在复数范围内无解.(×) (2)复数z=M+bi(a,b∈R)中,虚部为bi(X) (3)复数中有相等复数的概念,因此复数可以比较大小.(×) (4)复平面内的坐标原点是实轴与虚轴的交点.(√) (⑤)复数的模实质上就是复平面内复数对应的点到原点的距 离,也就是复数对应的向量的长度(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√” ,错误 的画“×” . (1)方程x2+x+5=0在复数范围内无解.( ) (2)复数z=a+bi(a,b∈R)中,虚部为bi.( ) (3)复数中有相等复数的概念,因此复数可以比较大小.( ) (4)复平面内的坐标原点是实轴与虚轴的交点.( ) (5)复数的模实质上就是复平面内复数对应的点到原点的距 离,也就是复数对应的向量的长度.( ) × × × √ √