
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 ( ) ( ) ( ) ( ) m s d g u p 1.32 10 / 1035 2.12 10 5 10 1010 1035 9.81 0.154 0.154 5 7 5 0.6 0.4 6 1.6 6 7 5 0.4 0.4 1.6 0 − − − = − × × × × × − × = × − = ρ µ ρ ρ 验算雷诺数: 3.22 10 1 2.12 10 5 10 1.32 10 1035 5 3 6 5 0 = × < × × × × × = = − − − − µ du ρ R ep 说明上述假定区域不正确。应再假定另一区域试算。 再假定沉降在层流区进行,按 Stockes 定律: ( ) ( ) m s d g u p 1.61 10 / 18 2.12 10 5 10 9.81 18 7 3 2 2 6 0 − − − = − × × × × × = − = µ ρ ρ 验算雷诺数: 3.93 10 1 2.12 10 5 10 1.61 10 1035 7 3 6 7 0 = × < × × × × × = = − − − − µ du ρ R ep 表明本次假定正确。所求得的 u0之值-1.61×10-7 ms-1 即为所 求的沉降速度。负号表示脂肪球向上浮。 (2)用直接法计算,由已知数据求 K ( ) ( ) ( ) 1.90 10 2.62 2.12 10 1.35 1010 1035 9.81 5 10 3 7 5 2 3 6 3 1 2 = × < × × − × = × × − = − − − µ ρ ρ ρ g K d p 由于 K〈2.62,可知沉降在层流区。可直接按公式计算,得 u0 11
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 ( ) ( ) ( ) ( ) m s d g u p 1.32 10 / 1035 2.12 10 5 10 1010 1035 9.81 0.154 0.154 5 7 5 0.6 0.4 6 1.6 6 7 5 0.4 0.4 1.6 0 − − − = − × × × × × − × = × − = ρ µ ρ ρ 验算雷诺数: 3.22 10 1 2.12 10 5 10 1.32 10 1035 5 3 6 5 0 = × < × × × × × = = − − − − µ du ρ R ep 说明上述假定区域不正确。应再假定另一区域试算。 再假定沉降在层流区进行,按 Stockes 定律: ( ) ( ) m s d g u p 1.61 10 / 18 2.12 10 5 10 9.81 18 7 3 2 2 6 0 − − − = − × × × × × = − = µ ρ ρ 验算雷诺数: 3.93 10 1 2.12 10 5 10 1.61 10 1035 7 3 6 7 0 = × < × × × × × = = − − − − µ du ρ R ep 表明本次假定正确。所求得的 u0之值-1.61×10-7 ms-1 即为所 求的沉降速度。负号表示脂肪球向上浮。 (2)用直接法计算,由已知数据求 K ( ) ( ) ( ) 1.90 10 2.62 2.12 10 1.35 1010 1035 9.81 5 10 3 7 5 2 3 6 3 1 2 = × < × × − × = × × − = − − − µ ρ ρ ρ g K d p 由于 K〈2.62,可知沉降在层流区。可直接按公式计算,得 u0 11

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 =-1.61X10-7 m/s 3. 影响沉降速度的因素 The influence factors on the settling velocity 多数沉降过程是在层流区内进行。根据层流区的 Stockes 定律, 从理论上可对影响沉降速度的因素作如下分析。 (1)颗粒直径(diameter of particles) 理论上沉降速度与 粒径的平方成正比。颗粒愈大,沉降就愈快。食品生产中的均质化处 理就是使悬浮颗粒或液滴微粒化,减慢沉降速度,达到制品稳定,不 易沉淀或分层目的的,例如牛奶和果汁的均质处理。另外,在食品加 工中,有时也采取适当措施增大颗粒直径、达到迅速沉降使制品澄清 的目的。如具有胶体性质的悬浮液食品,常采用加热的方法产生絮凝 作用,达到使颗粒增大易沉淀析出的目的。 (2) 分散介质粘度(Viscosity of dispersed medium) 沉降速 度与介质的粘度成反比。介质的粘度愈大,悬浮液愈难于用沉降法分 离。如含有果胶的果汁,因其粘度高,在生产中常通过加酶制剂破坏 果胶来降低其粘度,达到改善澄清操作的目的。此外,还有利用适当 加热的办法来降低粘度,达到加快沉降速度的目的。 (3) 两相密度差 (Density difference between two phases) 沉降速度与两相密度差成正比。但在一定的悬浮液的沉降分离过程 中,其值是难以改变的。 除了上述直接的影响因素外,实际的沉降过程还受其它因素的影 响。因前面讨论的自由沉降是基于光滑球形颗粒在无限连续的介质中 12
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 =-1.61X10-7 m/s 3. 影响沉降速度的因素 The influence factors on the settling velocity 多数沉降过程是在层流区内进行。根据层流区的 Stockes 定律, 从理论上可对影响沉降速度的因素作如下分析。 (1)颗粒直径(diameter of particles) 理论上沉降速度与 粒径的平方成正比。颗粒愈大,沉降就愈快。食品生产中的均质化处 理就是使悬浮颗粒或液滴微粒化,减慢沉降速度,达到制品稳定,不 易沉淀或分层目的的,例如牛奶和果汁的均质处理。另外,在食品加 工中,有时也采取适当措施增大颗粒直径、达到迅速沉降使制品澄清 的目的。如具有胶体性质的悬浮液食品,常采用加热的方法产生絮凝 作用,达到使颗粒增大易沉淀析出的目的。 (2) 分散介质粘度(Viscosity of dispersed medium) 沉降速 度与介质的粘度成反比。介质的粘度愈大,悬浮液愈难于用沉降法分 离。如含有果胶的果汁,因其粘度高,在生产中常通过加酶制剂破坏 果胶来降低其粘度,达到改善澄清操作的目的。此外,还有利用适当 加热的办法来降低粘度,达到加快沉降速度的目的。 (3) 两相密度差 (Density difference between two phases) 沉降速度与两相密度差成正比。但在一定的悬浮液的沉降分离过程 中,其值是难以改变的。 除了上述直接的影响因素外,实际的沉降过程还受其它因素的影 响。因前面讨论的自由沉降是基于光滑球形颗粒在无限连续的介质中 12

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 并为颗粒间互不影响而沉降的假设。实际上,介质并非无限量,沉降 都是在有限容器中进行,颗粒间有干扰,颗粒并非球形,而且大小、 形状各异。因此,实际沉降速度还受下面诸因素的影响。 (1) 颗粒形状(Shape of particles) 球形颗粒对任何方向的 来流都具有相同的投影面积。非球形则不同,偏离球形愈大,亦即球 形度φs愈小,阻力系数ξ愈大。几种φS值下的阻力系数ξ与雷诺数 Rep的关系曲线已根据实验结果标绘在图 4—2 中。对非球形颗粒,Rep 计算式中的 d 应该使用颗粒的体积当量直径。 (2) 壁效应(Wall effect) 在实际有限的容器中进行沉降,器 壁对颗粒沉降有阻滞作用,使沉降速度较自由沉降速度为小,这种影 响称为壁效应。需作准确计算时,应考虑壁效应的影响。 (3) 干扰沉降 (hindered settling) 当非均匀混合物中分散 颗粒较多,颗粒之间互相距离较近时,颗粒间的碰撞和摩擦作用会消 耗功能,亦即增加了阻力系数,使沉降速度较自由沉降时低,这种沉 降称为干扰沉降。悬浮液的沉聚一般为干扰沉降,其浓度愈高,此种 现象愈显著。通常干扰沉降速度仍按自由沉降计算,必要时可用经验 法则予以修正。 4—2 悬浮液的重力沉降 Gravity settling of the suspension 悬浮液的重力沉降,按其沉降是获得清液和增浓制品目的的不 同,可分别称为澄清(clarifying)和增稠(thickening);按其操作 方式可分为间歇式、半连续式和连续式。间歇式操作是将悬浮液贮于 容器内,经一定时间的静置,将上层澄清液引出后,卸出沉于器底的 13
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 并为颗粒间互不影响而沉降的假设。实际上,介质并非无限量,沉降 都是在有限容器中进行,颗粒间有干扰,颗粒并非球形,而且大小、 形状各异。因此,实际沉降速度还受下面诸因素的影响。 (1) 颗粒形状(Shape of particles) 球形颗粒对任何方向的 来流都具有相同的投影面积。非球形则不同,偏离球形愈大,亦即球 形度φs愈小,阻力系数ξ愈大。几种φS值下的阻力系数ξ与雷诺数 Rep的关系曲线已根据实验结果标绘在图 4—2 中。对非球形颗粒,Rep 计算式中的 d 应该使用颗粒的体积当量直径。 (2) 壁效应(Wall effect) 在实际有限的容器中进行沉降,器 壁对颗粒沉降有阻滞作用,使沉降速度较自由沉降速度为小,这种影 响称为壁效应。需作准确计算时,应考虑壁效应的影响。 (3) 干扰沉降 (hindered settling) 当非均匀混合物中分散 颗粒较多,颗粒之间互相距离较近时,颗粒间的碰撞和摩擦作用会消 耗功能,亦即增加了阻力系数,使沉降速度较自由沉降时低,这种沉 降称为干扰沉降。悬浮液的沉聚一般为干扰沉降,其浓度愈高,此种 现象愈显著。通常干扰沉降速度仍按自由沉降计算,必要时可用经验 法则予以修正。 4—2 悬浮液的重力沉降 Gravity settling of the suspension 悬浮液的重力沉降,按其沉降是获得清液和增浓制品目的的不 同,可分别称为澄清(clarifying)和增稠(thickening);按其操作 方式可分为间歇式、半连续式和连续式。间歇式操作是将悬浮液贮于 容器内,经一定时间的静置,将上层澄清液引出后,卸出沉于器底的 13

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 沉淀;半连续式操作是将悬浮液以较小的流速连续流过沉降器,或以 一定流速流过相当长的沉降槽,保证其颗粒有充分时间沉于器底,而 器底沉淀的卸出则为间歇式;如果悬浮液是连续送入沉降器,且清液 和沉淀亦连续排出,则为连续式操作。 4.2A 间歇式沉降器 Batch-type thickener 在间歇式沉降器内,整个物料从沉降开始至终了实际上是静止而 不流动,悬浮液的进入和沉淀的排出是间歇进行。 图 4—4(1)表示一种带锥底的圆形沉降器,在器内不同高度的侧 壁上装几个侧管,并配有阀,以引出清液。例如糖厂使用的三管阀式 淀淀器。也可采用虹吸方法引出清液。一般当一批物料沉降完毕后, 先引出清液而后卸出沉淀。对于乳浊液的分离,例如油水的分离,上 层为增浓制品,下层为清液,可将上层增浓制品先行引出,而后卸出 清液。 典型的间歇式沉降过程示于图 4—4(2)中。当颗粒粒径分布较均 匀时,操作开始不久就出现清液区 A 和悬液区 B 之间明显的界限,而 底部只有少量的沉淀层,称为沉聚区 C。当 A~B 界面和 B~C 界面相 距甚大时,A~B 界面就以匀速向下移动。区域 B 内的浓度因该区域 整体下沉而保持不变。这样清液区 A 和沉聚区 C 随时间不断扩大,而 区域 B 则不断缩小。最后区域 B 完全消失,仅留下清液区 A 和沉淀区 C。此后,沉聚区 C 内的固体沉淀物继续被压紧,并不断游离出清液。 间歇式重力沉降在食品工业上的应用较少,只用于少量悬浮液或 者沉降速度极为缓慢的情形,如葡萄酒和果汁的澄清等。 14
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 沉淀;半连续式操作是将悬浮液以较小的流速连续流过沉降器,或以 一定流速流过相当长的沉降槽,保证其颗粒有充分时间沉于器底,而 器底沉淀的卸出则为间歇式;如果悬浮液是连续送入沉降器,且清液 和沉淀亦连续排出,则为连续式操作。 4.2A 间歇式沉降器 Batch-type thickener 在间歇式沉降器内,整个物料从沉降开始至终了实际上是静止而 不流动,悬浮液的进入和沉淀的排出是间歇进行。 图 4—4(1)表示一种带锥底的圆形沉降器,在器内不同高度的侧 壁上装几个侧管,并配有阀,以引出清液。例如糖厂使用的三管阀式 淀淀器。也可采用虹吸方法引出清液。一般当一批物料沉降完毕后, 先引出清液而后卸出沉淀。对于乳浊液的分离,例如油水的分离,上 层为增浓制品,下层为清液,可将上层增浓制品先行引出,而后卸出 清液。 典型的间歇式沉降过程示于图 4—4(2)中。当颗粒粒径分布较均 匀时,操作开始不久就出现清液区 A 和悬液区 B 之间明显的界限,而 底部只有少量的沉淀层,称为沉聚区 C。当 A~B 界面和 B~C 界面相 距甚大时,A~B 界面就以匀速向下移动。区域 B 内的浓度因该区域 整体下沉而保持不变。这样清液区 A 和沉聚区 C 随时间不断扩大,而 区域 B 则不断缩小。最后区域 B 完全消失,仅留下清液区 A 和沉淀区 C。此后,沉聚区 C 内的固体沉淀物继续被压紧,并不断游离出清液。 间歇式重力沉降在食品工业上的应用较少,只用于少量悬浮液或 者沉降速度极为缓慢的情形,如葡萄酒和果汁的澄清等。 14
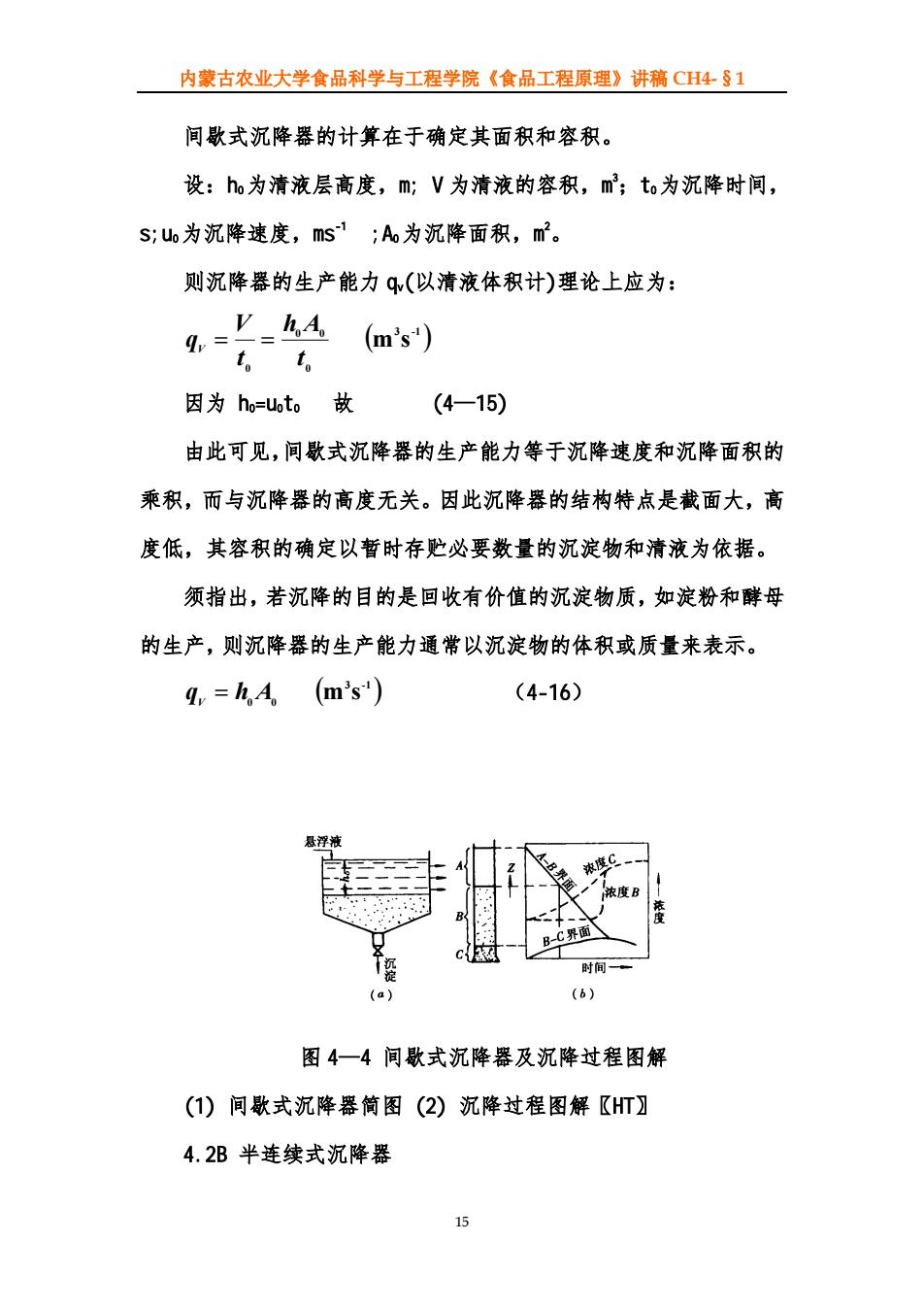
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 间歇式沉降器的计算在于确定其面积和容积。 设:h0为清液层高度,m; V 为清液的容积,m3 ;t0为沉降时间, s;u0为沉降速度,ms-1 ;A0为沉降面积,m2 。 则沉降器的生产能力 qv(以清液体积计)理论上应为: ( ) 3 -1 0 0 0 0 m s t h A t V qV = = 因为 h0=u0t0 故 (4—15) 由此可见,间歇式沉降器的生产能力等于沉降速度和沉降面积的 乘积,而与沉降器的高度无关。因此沉降器的结构特点是截面大,高 度低,其容积的确定以暂时存贮必要数量的沉淀物和清液为依据。 须指出,若沉降的目的是回收有价值的沉淀物质,如淀粉和酵母 的生产,则沉降器的生产能力通常以沉淀物的体积或质量来表示。 ( ) 3 -1 0 0 q h A m s V = (4-16) 图 4—4 间歇式沉降器及沉降过程图解 (1) 间歇式沉降器简图 (2) 沉降过程图解〖HT〗 4.2B 半连续式沉降器 15
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 间歇式沉降器的计算在于确定其面积和容积。 设:h0为清液层高度,m; V 为清液的容积,m3 ;t0为沉降时间, s;u0为沉降速度,ms-1 ;A0为沉降面积,m2 。 则沉降器的生产能力 qv(以清液体积计)理论上应为: ( ) 3 -1 0 0 0 0 m s t h A t V qV = = 因为 h0=u0t0 故 (4—15) 由此可见,间歇式沉降器的生产能力等于沉降速度和沉降面积的 乘积,而与沉降器的高度无关。因此沉降器的结构特点是截面大,高 度低,其容积的确定以暂时存贮必要数量的沉淀物和清液为依据。 须指出,若沉降的目的是回收有价值的沉淀物质,如淀粉和酵母 的生产,则沉降器的生产能力通常以沉淀物的体积或质量来表示。 ( ) 3 -1 0 0 q h A m s V = (4-16) 图 4—4 间歇式沉降器及沉降过程图解 (1) 间歇式沉降器简图 (2) 沉降过程图解〖HT〗 4.2B 半连续式沉降器 15