
Ch.7 Spin and undistinguished similar particles 轨道角动量 自旋角动量 ixi=int, §x ihS [i:,L,]=ihi, [S::S,]=ihs: [Ev,L.]=inis [S,.S:1=ins, [E:,L:]=iht, IS.,S,1=ins 由于自旋角动量在空间任意方向上的投影只能取±/2两个值 所以S、S、 的本征值都是±/2,其平方为[/2]2 算符的本征值是:S2=$2+S3+S?=2
11 Ch.7 Spin and undistinguished similar particles ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ , ˆ ˆ ˆ ˆ ˆ ˆ [ , ] [ , ] , ˆ ˆ ˆ ˆ ˆ ˆ [ , ] , [ , ] ˆ ˆ ˆ ˆ ˆ ˆ [ , ] [ , ] x y z x y z y z x y z x z x y z x y L S L L i L S S i S L L i L S S i S L L i L S S i S L L i L S S i S × = × = ⎧ = ⎧ = ⎪ ⎪ ⎪ ⎪ ⎨ ⎨ = = ⎪ ⎪ ⎪ ⎪ = = ⎩ ⎩ G G G G G G G G = = = = = = = = 轨道角动量 自 旋角动量 由于自旋角动量在空间任意方向上的投影只能取±=/2两个值 所以 ˆ ˆ ˆ x y z S S 、 、S 的本征值都是±=/2,其平方为[=/2]2 ˆ 2 S 算符的本征值是: 2 4 ˆ 2 ˆ 2 ˆ 2 ˆ 2 3 = + + = = x y z S S S S
Ch.7 Spin and undistinguished similar particles 仿照:=11+1)2> S2=s(s+1)2=, S 自旋量子数s只有一个数值 S= 2 0 12
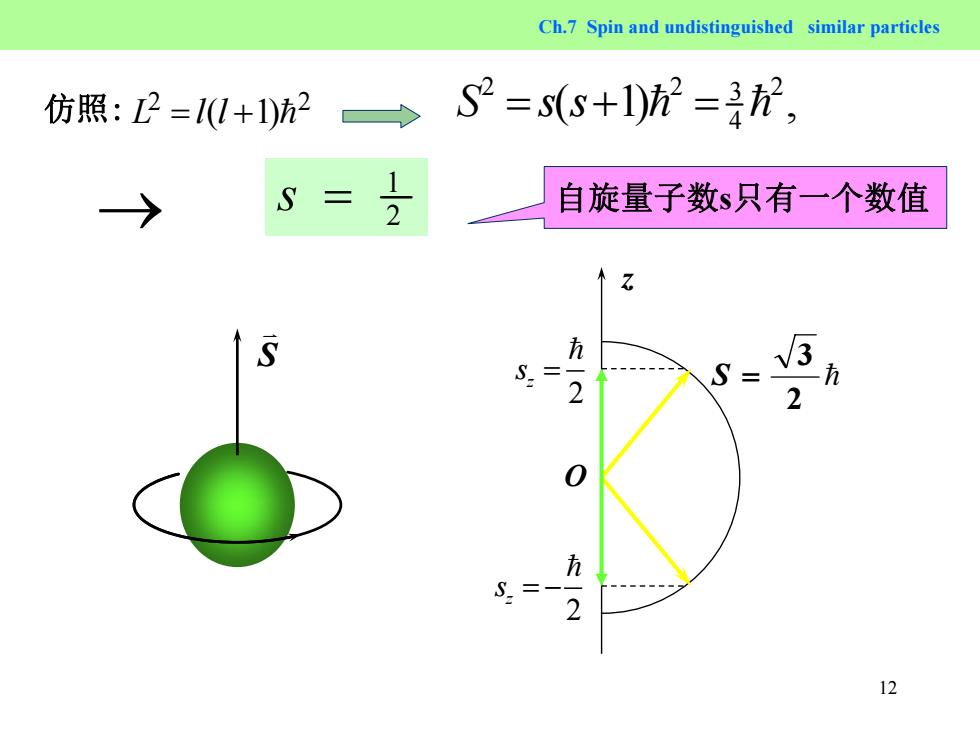
12 Ch.7 Spin and undistinguished similar particles S K = 2 3 S = 2 z s = − = 2 z s = = z O 仿照: 2 2 L = l(l +1)= 2 2 3 2 4 S s = + ( 1 s )= = = , 自旋量子数s只有一个数值 12 → s =

Ch.7 Spin and undistinguished similar particles (二)含自旋的状态波函数 因为自旋是电子内部运动自由度,所以描写电子运动除了 用(x,y,)三个坐标变量外,还需要一个自旋变量(S2),于 是电子的含自旋的波函数需写为: Ψ=Ψ(x,y,z,Sz,t) Ψ1(F,t)=平(x,y,+,t) 由于S2只取士/2两个值, Ψ2(F,t)=Ψ(x,y,z,-,t) 所以上式可写为两个分量: 规定列矩阵: 写成列矩阵: Φ= 9(f,t) 第一行对应于S,=/2, 92(f,t) 第二行对应于S,=-/2。 若已知电子处于S,=/2或S,=-/2的自旋态,则波函数可分 别写为: 13
13 Ch.7 Spin and undistinguished similar particles 因为自旋是电子内部运动自由度,所以描写电子运动除了 用 (x, y, z) 三个坐标变量外,还需要一个自旋变量 (SZ),于 是电子的含自旋的波函数需写为: ( x, y, z, S , t) Ψ = Ψ z 由于SZ 只取±=/2两个值, 所以上式可写为两个分量: ⎩⎨⎧ = Ψ − = Ψ + ( , ) ( , , , , ) ( , ) ( , , , , ) 2 2 1 2 r t x y z t r t x y z t == GG ψψ (二)含自旋的状态波函数 写成列矩阵: ⎟⎟⎠⎞ ⎜⎜⎝⎛ Φ = ( , ) ( , ) 21 r t r t GG ψψ 规定列矩阵: 第一行对应于 Sz = =/2, 第二行对应于 Sz = -=/2。 若已知电子处于Sz = =/2 或 Sz = -=/2的自旋态,则波函数可分 别写为: 1 1 2 2 1 2 ( , ) 0 , 0 ( , ) r t r t ψ ψ − ⎛ ⎞ ⎛ ⎞ Φ = ⎜ ⎟ Φ = ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ G G

Ch.7 Spin and undistinguished similar particles 三)自旋算符的矩阵表示与Pauli矩阵 (1)Sz的矩阵形式: 电子自旋算符(如S)是作用于电子自旋波函数上的,既然电 子波函数表示成了2×1的列矩阵,那末,电子自旋算符的矩 阵表示应该是2×2矩阵: d 因为中2描写的态中Sz有确定值/2,所以中12是S2的本征 态,本征值为2,即有: 矩阵形式: G”-60) 14
14 Ch.7 Spin and undistinguished similar particles (1) SZ的矩阵形式: 电子自旋算符(如SZ)是作用于电子自旋波函数上的,既然电 子波函数表示成了2×1 的列矩阵,那末,电子自旋算符的矩 阵表示应该是 2×2 矩阵: 2 z a b S c d ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ = (三)自旋算符的矩阵表示与 Pauli 矩阵 因为Φ1/2 描写的态中SZ有确定值 =/2,所以Φ1/2 是 SZ 的本征 态,本征值为 =/2,即有: 1 1 2 2 2 z S Φ = Φ= 矩阵形式: 1 1 ( , ) ( , ) 2 2 0 0 a b r t r t c d ⎛ ⎞⎛ψ ψ ⎞ ⎛ ⎞ ⎜ ⎟⎜ ⎟ = ⎜ ⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠ G G = =

Ch.7 Spin and undistinguished similar particles 份一 问E对烧题布g以G气 b=0 d=-1 最后得S,的矩阵形式: S2是对角矩阵,对角矩阵元是其本征值±/2。 15
15 Ch.7 Spin and undistinguished similar particles 1 1 1 0 a c ψ ψ ψ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎩⎨⎧ == 01 ca 同理对Φ–1/2 处理,有: 2 2 0 0 2 2 ( , ) ( , ) a b c d ψ ψ r t r t ⎛ ⎞⎛ ⎞ ⎛ ⎞ ⎜ ⎟⎜ ⎟ = − ⎜ ⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠ = = G G 2 2 2 b 0 d ψ ψ ψ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ = −⎜ ⎟ ⎝ ⎠ ⎝ ⎠ 0 1 bd⎧ = ⎨⎩ = − 最后得 SZ 的矩阵形式: 1 0 2 0 1 z S ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ − = SZ 是对角矩阵,对角矩阵元是其本征值±=/2