
方法,就会迎来更大的发展。 课程目标4:能够利用积分知识归纳总结实验数据:能够利用不定积分解决问题,并得 到有效结论:能由边际函数求原函数。 课程目标5:能应用定积分判断一些函数的可积性(包括可积函数类):能应用定积分 表达一些几句量、物理量、经济量的方法:能够利用定积分化整为零的原理分析实际问顺, 并具备利用定积分解决实际问题的自主学习能力:能建立“变与不变”、“近似与精确”、“有 限与无限”、“量变与质变”等辩证唯物主义思想。 (三)课程目标和毕业要求的对应关系 (说明:学科基础课程目标需兼顾共性和专业特色。个性化课程目标根据授课对象所属 专业的培养方案矩阵中课程对应的毕业要求一级指标确定) 谏程目标 毕业要求指标点 毕业要求 1 能熟练掌握数学的理论和方法:针对具体的问愿建立模型并进行科学分 基础理论 析:具有科学素养和科学态度 2 、统计学用于相关专业领城复杂问避的表述:能够将相关知识 2.专业知识 和计量经济模型方法用于研究经济管理领域复杂问: 能够采用定性或定量方法描述会计相关领域的专业问题:能够识别、表 达、并通过现代工具分析金融机构业务运作:能将数学理论与方法用」 3间模分析 食品经济管理领域复杂问题的研究和分析。 能够具有持续学习的能力:能够具有自主学习的能力。 10.终身学习 熟练掌提问愿分析工具、创新思维工具:能运用现代化信总技术工具, 5.现代工具使用 提高工作效率。 三、教学内容、要求与学时分配 在承载课程思政目标的有关章节的教学内容中明确课程思政融入点,阐述预期学习成果, 不承担课程思政目标的章节中无需填写。授课对象不同,授课内容、重难点、学时分配、教 学方式等应有所侧重 教学内容 预期学习成果 重点、难点 程目标 第一章函数与极限 (1)函数 能建立变量数学的思想 重点:函数、极限和连 无穷大 续的根念 、极限运算 能够运用严格数学语目 (5》报限标算法 则、闭区间上连续函划 (6)极限存在准则两个重要极限 论证极限间题:能从中因 线上、线下 的性质 22 1 古代的极限思想建立民 (7》无穷小的比 混合式教学 族自章感和责任感,民族 难点:极限和连续的概 算与初等函数的 凝聚力 续性 (10)闭区间上连续函数的性质 思政融入点:中国古代的极限思想 15
15 方法,就会迎来更大的发展。 课程目标 4:能够利用积分知识归纳总结实验数据;能够利用不定积分解决问题,并得 到有效结论;能由边际函数求原函数。 课程目标 5:能应用定积分判断一些函数的可积性(包括可积函数类);能应用定积分 表达一些几何量、物理量、经济量的方法;能够利用定积分化整为零的原理分析实际问题, 并具备利用定积分解决实际问题的自主学习能力;能建立“变与不变”、“近似与精确”、“有 限与无限”、“量变与质变”等辩证唯物主义思想。 (三)课程目标和毕业要求的对应关系 (说明:学科基础课程目标需兼顾共性和专业特色。个性化课程目标根据授课对象所属 专业的培养方案矩阵中课程对应的毕业要求一级指标确定) 课程目标 毕业要求指标点 毕业要求 1 能熟练掌握数学的理论和方法;针对具体的问题建立模型并进行科学分 析;具有科学素养和科学态度。 1.基础理论 2 能将数学、统计学用于相关专业领域复杂问题的表述;能够将相关知识 和计量经济模型方法用于研究经济管理领域复杂问题; 2.专业知识 3 能够采用定性或定量方法描述会计相关领域的专业问题;能够识别、表 达、并通过现代工具分析金融机构业务运作;能将数学理论与方法用于 食品经济管理领域复杂问题的研究和分析。 3.问题分析 4 能够具有持续学习的能力;能够具有自主学习的能力。 10.终身学习 5 熟练掌握问题分析工具、创新思维工具;能运用现代化信息技术工具, 提高工作效率。 5.现代工具使用 三、教学内容、要求与学时分配 在承载课程思政目标的有关章节的教学内容中明确课程思政融入点,阐述预期学习成果, 不承担课程思政目标的章节中无需填写。授课对象不同,授课内容、重难点、学时分配、教 学方式等应有所侧重。 教学内容 预期学习成果 重点、难点 学时 教学方式(讲 授、实验、上 机、讨论) 支撑课 程目标 第一章 函数与极限 (1)函数 (2)数列的极限 (3)函数的极限 (4)无穷小与无穷大 (5)极限运算法则 (6)极限存在准则 两个重要极限 (7)无穷小的比较 (8)函数的连续性 (9)连续函数的运算与初等函数的 连续性 (10)闭区间上连续函数的性质 思政融入点:中国古代的极限思想 能建立变量数学的思想, 能够运用严格数学语言 论证极限问题;能从中国 古代的极限思想建立民 族自豪感和责任感,民族 凝聚力。 重点:函数、极限和连 续的概念、极限运算法 则、闭区间上连续函数 的性质 难点:极限和连续的概 念 22 线上、线下 混合式教学 1
教学内容 预期学习成果 重点、难点 散学方式(训支掉课 学时授、实验、上 机、讨论)程目标 重点:导数和微分的榈 念、导数的四则运算, 能这远用极明用却分好有合帝的象是法则 第二章导数与微分 司题,并利用所学数 基本初等函数的导数 (1)导数的越今 (2)导数的求导法则 续、可导相关数学知 式 反函数的导数 12 线上、线下 立简单的数学模型,能用 函数和参数式所确定的 2 (3)高阶导划 混合式教学 函数的导数求边际函数 函数的导数 (4)隐函数及参数方程求导 和弹性函数,并能解释其 (5)函数的微分 经济意义。 难点:复合函数、隐函 重点:罗尔定理、拉格 第三章微分中值定理与导数的应用 们日中值定理、函数的 (1)微分中值定理 能应用导数正确地作出 单调性、极值、最值 (2》洛以法法则 弱数图象:能就利用表制 洛以达法叫 (3)泰物公式 展式来识别判断实际 线上、线下 (4)函数的单调性与曲线的凹凸性 14 3 程及经济间题,用函数秘 混合式教学 难点:罗尔定理、拉格 (5)函数的极值与最大值最小值 值概念讨论优化问题:认 朗日中值定理、柯西中 (6)函数图形的描绘 国危机与机遇并存。 值定理、最值应用问题 思政融入点:数学发展的三次危机 泰勒公式 第四章不定积分 重点:不定积分的 能够利用积分知识归邹 与性质、不定积分的换 (1)不定积分的概念与性切 总结实验数据:能够利用元法与分部积分法 线上、线下 (2)换元积分法 10 4 不定积分解决问题,并得 混合式教学 (3)分部积分法 (4)有理函数的积分 到有效结论。 难点,不定积分的换示 分部积分 能应用定积分判断 重点:定积分的概念与 第五章定积分 雨数的可积性(包括可积性质,定积分的换元法 (1)定积分的概念与性质 承数类):能馆利用定积积分上限的承数及其三 (2)微积分基本公式 分化整为零的原理分析 数、牛顿.莱布尼线公 (3》定积分的换元积分法和分部积 实际问,并具备利用 式、广义积分 14 线上、线下 5 (4)广义积分 识分解决实际问的目 混合式教学 生学习能力:现实世界 难点:定积分的概念 思政融入点:“变与不变”“、近似与 的静证法里想在数学越定积分的艳元法。积 站确”“,有限与无限”“、量变与 诊和公式的学习中得到 上限的函数及其导数 变”等样证唯物主义思相 充分的体现 广义分 重点:平面图形的面积 第六章定积分的应用 旋转休的体积 能应用定积分表达一些 (1》定积分的微元法 线上、线下 5 几何量与物理量的方法 混合式教学 (2》定积分在几何上的应用 难点:平面图形的面彩 旋转休的体积 6
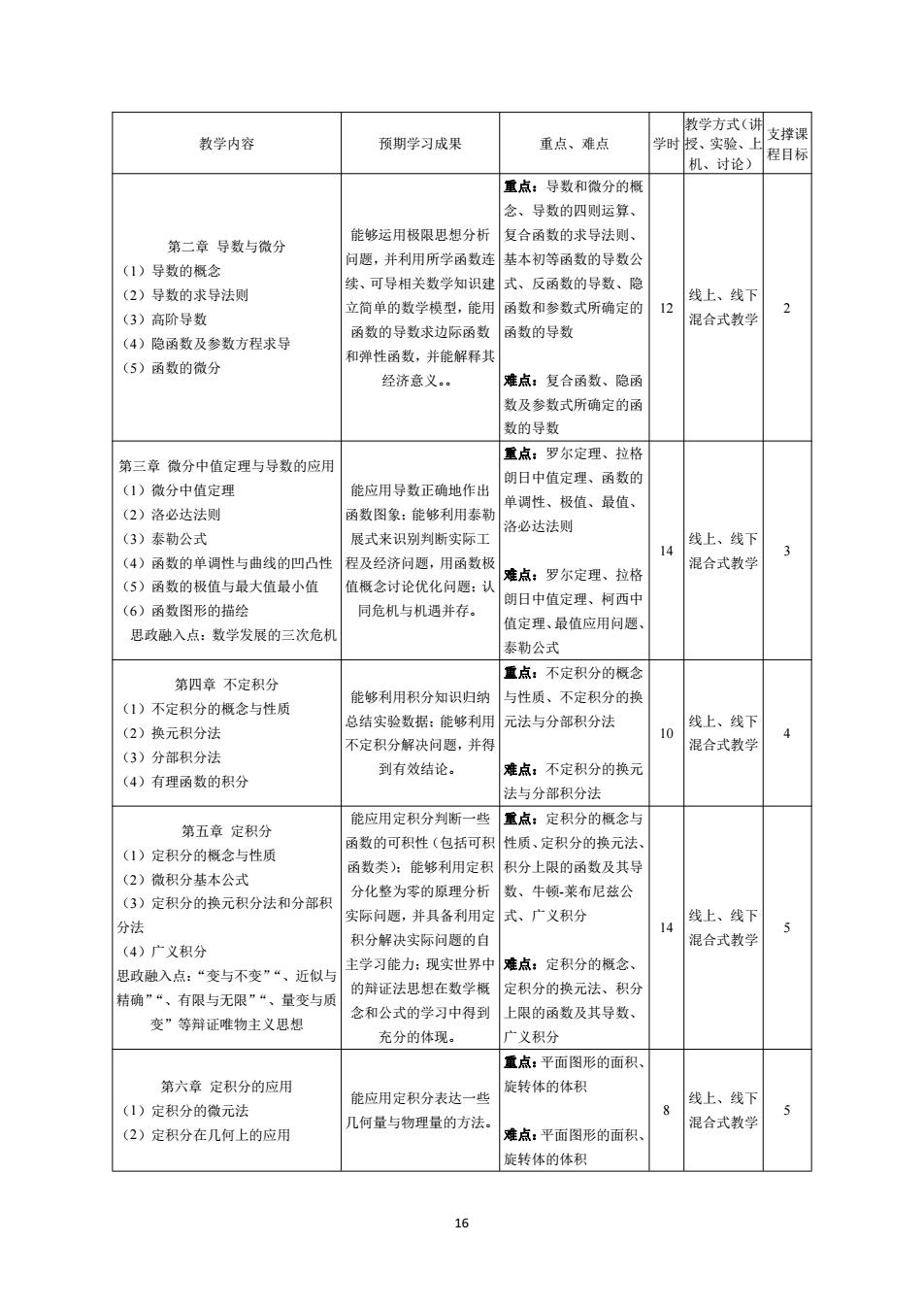
16 教学内容 预期学习成果 重点、难点 学时 教学方式(讲 授、实验、上 机、讨论) 支撑课 程目标 第二章 导数与微分 (1)导数的概念 (2)导数的求导法则 (3)高阶导数 (4)隐函数及参数方程求导 (5)函数的微分 能够运用极限思想分析 问题,并利用所学函数连 续、可导相关数学知识建 立简单的数学模型,能用 函数的导数求边际函数 和弹性函数,并能解释其 经济意义。。 重点:导数和微分的概 念、导数的四则运算、 复合函数的求导法则、 基本初等函数的导数公 式、反函数的导数、隐 函数和参数式所确定的 函数的导数 难点:复合函数、隐函 数及参数式所确定的函 数的导数 12 线上、线下 混合式教学 2 第三章 微分中值定理与导数的应用 (1)微分中值定理 (2)洛必达法则 (3)泰勒公式 (4)函数的单调性与曲线的凹凸性 (5)函数的极值与最大值最小值 (6)函数图形的描绘 思政融入点:数学发展的三次危机 能应用导数正确地作出 函数图象;能够利用泰勒 展式来识别判断实际工 程及经济问题,用函数极 值概念讨论优化问题;认 同危机与机遇并存。 重点:罗尔定理、拉格 朗日中值定理、函数的 单调性、极值、最值、 洛必达法则 难点:罗尔定理、拉格 朗日中值定理、柯西中 值定理、最值应用问题、 泰勒公式 14 线上、线下 混合式教学 3 第四章 不定积分 (1)不定积分的概念与性质 (2)换元积分法 (3)分部积分法 (4)有理函数的积分 能够利用积分知识归纳 总结实验数据;能够利用 不定积分解决问题,并得 到有效结论。 重点:不定积分的概念 与性质、不定积分的换 元法与分部积分法 难点:不定积分的换元 法与分部积分法 10 线上、线下 混合式教学 4 第五章 定积分 (1)定积分的概念与性质 (2)微积分基本公式 (3)定积分的换元积分法和分部积 分法 (4)广义积分 思政融入点:“变与不变”“、近似与 精确”“、有限与无限”“、量变与质 变”等辩证唯物主义思想 能应用定积分判断一些 函数的可积性(包括可积 函数类);能够利用定积 分化整为零的原理分析 实际问题,并具备利用定 积分解决实际问题的自 主学习能力;现实世界中 的辩证法思想在数学概 念和公式的学习中得到 充分的体现。 重点:定积分的概念与 性质、定积分的换元法、 积分上限的函数及其导 数、牛顿-莱布尼兹公 式、广义积分 难点:定积分的概念、 定积分的换元法、积分 上限的函数及其导数、 广义积分 14 线上、线下 混合式教学 5 第六章 定积分的应用 (1)定积分的微元法 (2)定积分在几何上的应用 能应用定积分表达一些 几何量与物理量的方法。 重点:平面图形的面积、 旋转体的体积 难点:平面图形的面积、 旋转体的体积 8 线上、线下 混合式教学 5
四、课程考核评价方式 考核以课程目标的达成度为主要目的,以检查学生对各知识点的掌握程度和应用能力为 重要内容。 (一)考核方式 考核方式为闭卷笔试。 考试课程成绩由期末成绩和平时成绩构成。 (二)课程成绩 平时成绩由在线学习成绩与课堂表现成绩构成,占总成绩的50%。 期末卷面成绩占50%。 1.考核环节及说明 成绩构成 考核说明 (1)平时成绩满分为100分,占总成绩的50% (2)其中在线学习成绩占总成绩的30%,学生需加入智慧树在线教有平台,完成高等数学乳上)》 经管类的全部内容学习,平台会根据学生的学习情况,给出在线课程成锁:课堂表现及课前 平时成绩 作业成绩占总成绩的20%,学生按照要求完成课前学习任务,遵守课堂规范,积极参与课堂 教学活动,认直完成小组任务,无扰乱课堂秩序的行为,本部分采用倒扣分数的原则,旷课、 未完成作业、抄袭作业,每次扣1分,直至20分全部扣完。 期末考试 (1)考试方式及占比:采用闭卷笔试,考试成绩100分,占课程考核成绩的50%。 (2)评定依据:考试成绩的评定根据试卷参考答案和评分标准进行。 (3)考试膜型:包含单项选择想、填空题、计算题等。 (4)考试内容:针对期末考试对应的课程日标,主要考核函数与极限、导数与微分、微分中值 定理与导数的应用、不定积分、定积分、定积分的应用等知识点的掌握程度。 2.考核与评价方式 成绩比例(%) 课程目标 平时成绩 合计 期末成绩 课堂表现 在线学习成绩 4 6 8 18 2 4 14 24 3 4 6 10 20 4 4 6 4 14 5 4 6 14 24 合计成绩构成) 20 30 350 100
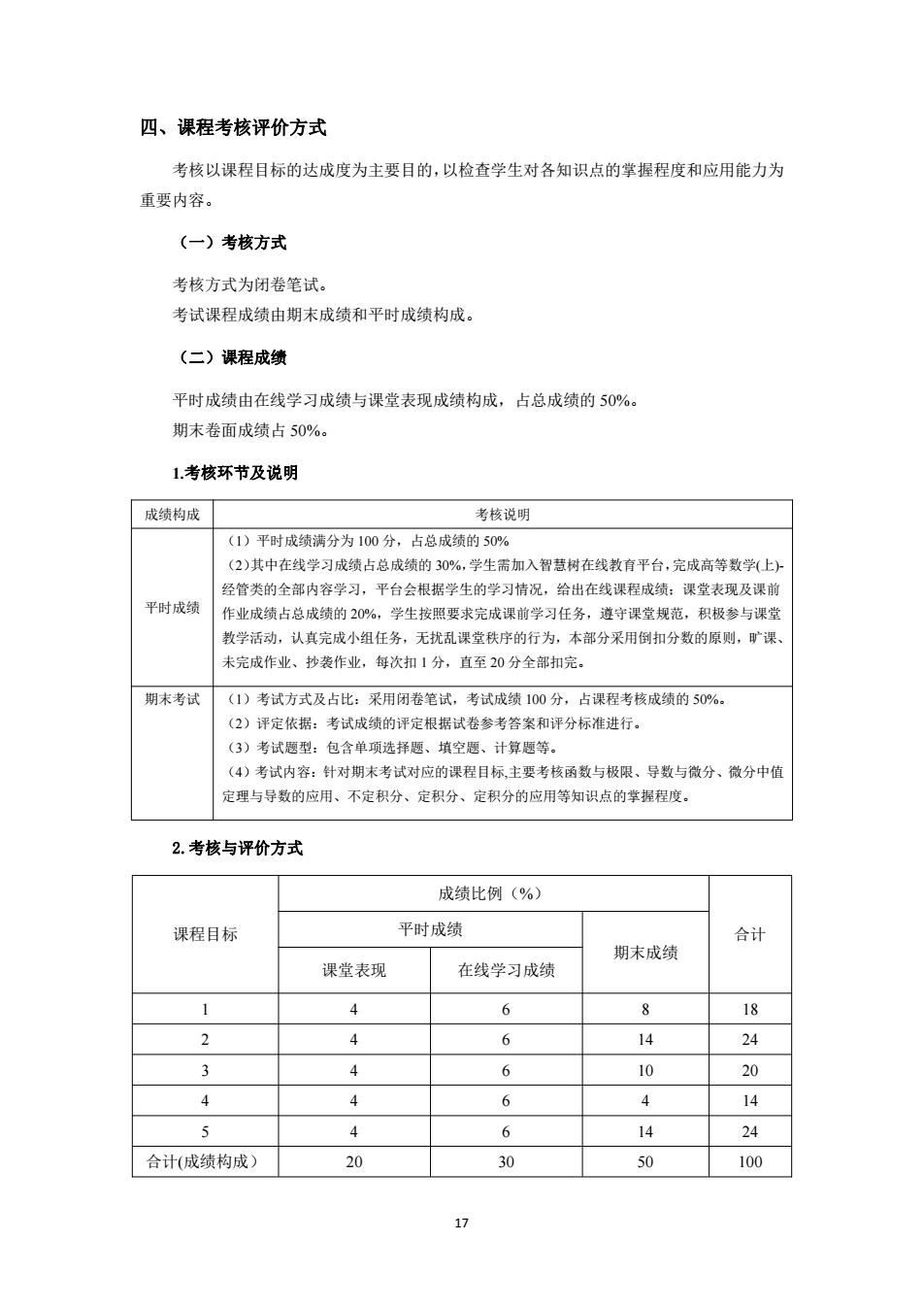
17 四、课程考核评价方式 考核以课程目标的达成度为主要目的,以检查学生对各知识点的掌握程度和应用能力为 重要内容。 (一)考核方式 考核方式为闭卷笔试。 考试课程成绩由期末成绩和平时成绩构成。 (二)课程成绩 平时成绩由在线学习成绩与课堂表现成绩构成,占总成绩的 50%。 期末卷面成绩占 50%。 1.考核环节及说明 成绩构成 考核说明 平时成绩 (1)平时成绩满分为 100 分,占总成绩的 50% (2)其中在线学习成绩占总成绩的 30%,学生需加入智慧树在线教育平台,完成高等数学(上)- 经管类的全部内容学习,平台会根据学生的学习情况,给出在线课程成绩;课堂表现及课前 作业成绩占总成绩的 20%,学生按照要求完成课前学习任务,遵守课堂规范,积极参与课堂 教学活动,认真完成小组任务,无扰乱课堂秩序的行为,本部分采用倒扣分数的原则,旷课、 未完成作业、抄袭作业,每次扣 1 分,直至 20 分全部扣完。 期末考试 (1)考试方式及占比:采用闭卷笔试,考试成绩 100 分,占课程考核成绩的 50%。 (2)评定依据:考试成绩的评定根据试卷参考答案和评分标准进行。 (3)考试题型:包含单项选择题、填空题、计算题等。 (4)考试内容:针对期末考试对应的课程目标,主要考核函数与极限、导数与微分、微分中值 定理与导数的应用、不定积分、定积分、定积分的应用等知识点的掌握程度。 2.考核与评价方式 课程目标 成绩比例(%) 平时成绩 合计 期末成绩 课堂表现 在线学习成绩 1 4 6 8 18 2 4 6 14 24 3 4 6 10 20 4 4 6 4 14 5 4 6 14 24 合计(成绩构成) 20 30 50 100

五、教学方法 本课程采用在线课程与传统课堂相结合的混合式授课方式,学生每天需完成当天的学习 任务,包括视频学习和课前作业。然后走进教室参与课堂教学。课前学习进行的是基础知识 的学习,课堂教学注重难点重点的学习,注重综合运用知识的能力。 六、参考材料 线上:智慧树: https://coursehome.zhihuishu.com/courseHome/1000006629/139136/18#teachTeam 线下: 1.《微积分(经济类)》(上下册) 吴赣昌主编,中国人民大学出版社,2017年7月第5 2.《高等数学》(上、下册),同济大学应用数学系编,高等教有出版社,2018年8月,第7 版 3.《托马斯微积分》,叶其孝、王耀东等译,高等教育出版社,2016年6月,第10版 4,《普林斯顿微积分读本》(美)阿德里安,班纳著杨爽等译人民邮电出版社2016 年10月 5.《微积分学习辅导与习题解答》吴赣昌主编,中国人民大学出版社,2018年9月第 5版 6.《高等数学附册学习辅导与习题选解》,同济大学应用数学系编,同济大学出版社,2014 年8月.第7版 7. 《微积分专题梳理与解读》邵剑李大侃同济大学出版社2011年6月. 8.《经济数学》霍伊等著张伟等译中国人民大学出版社2015年7月第3版. 9.《高等数学教与学参考》,主编:张宏志,西北工业大学出版社,2017年9月,第1版 主撰人:王晓明 审核人:刘太岗、王晓明 英文校对:王晓明 教学副院长:袁红春 日期:2022年9月10日
18 五、教学方法 本课程采用在线课程与传统课堂相结合的混合式授课方式,学生每天需完成当天的学习 任务,包括视频学习和课前作业。然后走进教室参与课堂教学。课前学习进行的是基础知识 的学习,课堂教学注重难点重点的学习,注重综合运用知识的能力。 六、参考材料 线上:智慧树: https://coursehome.zhihuishu.com/courseHome/1000006629/139136/18#teachTeam 线下: 1. 《微积分(经济类)》(上下册) 吴赣昌主编,中国人民大学出版社,2017 年 7 月第 5 版. 2. 《高等数学》(上、下册), 同济大学应用数学系编,高等教育出版社,2018 年 8 月,第 7 版. 3. 《托马斯微积分》, 叶其孝、王耀东等译, 高等教育出版社, 2016 年 6 月,第 10 版. 4. 《普林斯顿微积分读本》 (美)阿德里安·班纳著 杨爽等译 人民邮电出版社 2016 年 10 月. 5. 《微积分-学习辅导与习题解答》 吴赣昌主编,中国人民大学出版社,2018 年 9 月第 5 版. 6. 《高等数学附册学习辅导与习题选解》, 同济大学应用数学系编,同济大学出版社, 2014 年 8 月,第 7 版. 7. 《微积分专题梳理与解读》 邵剑 李大侃 同济大学出版社 2011 年 6 月. 8. 《经济数学》 霍伊等著 张伟等译 中国人民大学出版社 2015 年 7 月第 3 版. 9. 《高等数学教与学参考》, 主编:张宏志, 西北工业大学出版社, 2017 年 9 月,第 1 版. 主撰人:王晓明 审核人:刘太岗、王晓明 英文校对:王晓明 教学副院长:袁红春 日 期:2022 年 9 月 10 日
附件:各类考核与评价标准表 1课堂表现评分标准 成绩 良好 及格 优秀 中等 不及格 (78≤分数< (60≤分数 课程目标 (分数290分) (68≤分数<78 (分数<60分】 0 68) 学习积极主动, 学习态度端 学习态度较端 不能按要求及 , 可以按 正,基本可以拟 能按照要求及时 时完成课前作 求及时完成课 要求及时完成 不能按要求及 完成课前作业。 业,很少主动 前作业。能认 课前作业。能 时完成课前作 理论课准备充 国答问题,正 听进,回答 直听进,回答 业。回答问 课程目标 分,认直听进 确回答问要左 司题拉为 (209% 题较为积极。 可正确回 定的难 不积极 能正确回答老师 本能正确回名 中极限的 度。对数学 老师问题 老市问题,基 本思想理解格 问题。能熟练学 极限的基本思 拖掌根数学中 能堂据数学中 在闲准, 标数学中损限的 想理解不够充 极限的基本思 极限的基本更 基木思想 物 分。 按照要求及时完 按照要求及日 基本可以按雪 不能按要求元 不能按要求完 成课前作业,理 完成课前作 求及时完成球 成课肌作业, 成课前作业, 论课准名东分, 业。理论课准 的作业。理论理 较少回答 回答问很 认真听进,回答 备较充分,认 准拉充分,边 题。堂据一阶 少。不能掌挥 积极。能 直听进,国答 直听进,同答 求导高 阶求导、京 课程目标 练掌握 句题较积极 较积极。 基术 隐函数方 阶求导 隐函 (20% 导、高阶求导 能掌握一阶 程求导的数 数方程求导日 隐函数方程求与 导、高阶求导、 导、高阶求导 思想和求解方 数学思思和求 的数学思妇和求 路承数方程求 隐函敲方程表 法存在一定困 解方法, 解方法 导的数学思想 导的数学思相 和求解方法 和求解方法 可以通过课程学 可以通过课程 基本可以通过 通过课程学习 对应用函数极 习熟练掌探函数 学习掌程函数 课程学习草热 掌架函数极值 值概念讨论优 课程目标3 极馆感令计论用 极值据含村论 属数极值唇今 幅令讨论律化 化问题掌握不 (209%) 化问夏 讨论优化问想 夏有一定闲 熟练应用积分奥 能够应用积分 基本能够应用 应用积分知识 应用积分知识 谍程目标4 识归纳总结实哈 知识归纳总结 积分知识归封 归纳总结实验 归纳总结实照 (20%) 据。 实心数据。 总结实验数据。 数据有一定困 数据掌探不 能熟练应用定积 能应用定积分 基本能应用定 应用定积分表 应用定积分表 分表达一些几付 表达一些几何 积分表达 些几何每 些几何 课程目标5 量与物理量的方 量与物理量的 几何量与物理 与物理量的 与物理量的刀 (20%) 法。 方法。 量的方法 法右 一定困 法掌不足
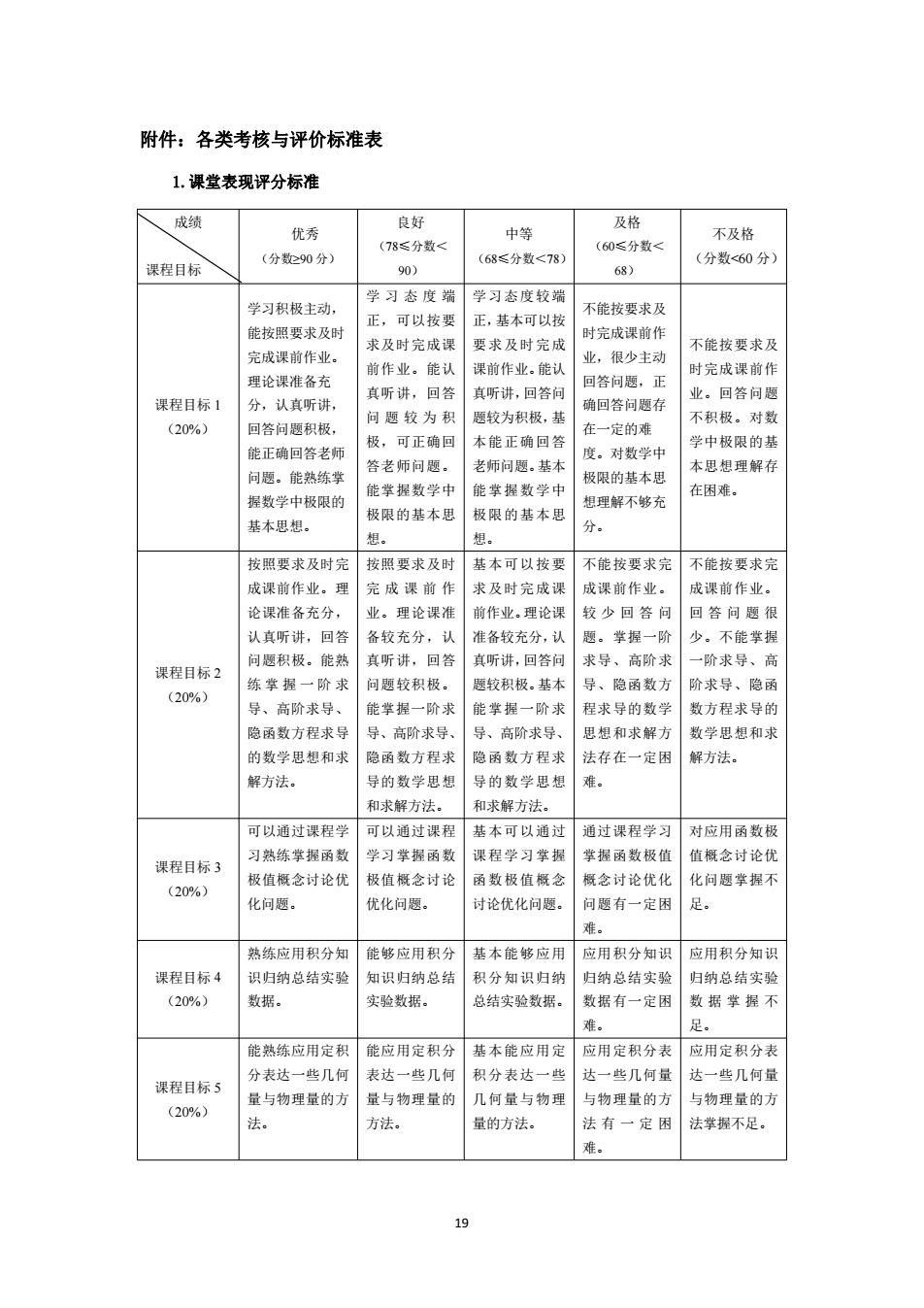
19 附件:各类考核与评价标准表 1.课堂表现评分标准 成绩 课程目标 优秀 (分数≥90 分) 良好 (78≤分数< 90) 中等 (68≤分数<78) 及格 (60≤分数< 68) 不及格 (分数<60 分) 课程目标 1 (20%) 学习积极主动, 能按照要求及时 完成课前作业。 理论课准备充 分,认真听讲, 回答问题积极, 能正确回答老师 问题。能熟练掌 握数学中极限的 基本思想。 学 习 态 度 端 正,可以按要 求及时完成课 前作业。能认 真听讲,回答 问 题 较 为 积 极,可正确回 答老师问题。 能掌握数学中 极限的基本思 想。 学习态度较端 正,基本可以按 要求及时完成 课前作业。能认 真听讲,回答问 题较为积极,基 本能正确回答 老师问题。基本 能掌握数学中 极限的基本思 想。 不能按要求及 时完成课前作 业,很少主动 回答问题,正 确回答问题存 在一定的难 度。对数学中 极限的基本思 想理解不够充 分。 不能按要求及 时完成课前作 业。回答问题 不积极。对数 学中极限的基 本思想理解存 在困难。 课程目标 2 (20%) 按照要求及时完 成课前作业。理 论课准备充分, 认真听讲,回答 问题积极。能熟 练 掌 握 一 阶 求 导、高阶求导、 隐函数方程求导 的数学思想和求 解方法。 按照要求及时 完 成 课 前 作 业。理论课准 备较充分,认 真听讲,回答 问题较积极。 能掌握一阶求 导、高阶求导、 隐函数方程求 导的数学思想 和求解方法。 基本可以按要 求及时完成课 前作业。理论课 准备较充分,认 真听讲,回答问 题较积极。基本 能掌握一阶求 导、高阶求导、 隐函数方程求 导的数学思想 和求解方法。 不能按要求完 成课前作业。 较 少 回 答 问 题。掌握一阶 求导、高阶求 导、隐函数方 程求导的数学 思想和求解方 法存在一定困 难。 不能按要求完 成课前作业。 回 答 问 题 很 少。不能掌握 一阶求导、高 阶求导、隐函 数方程求导的 数学思想和求 解方法。 课程目标 3 (20%) 可以通过课程学 习熟练掌握函数 极值概念讨论优 化问题。 可以通过课程 学习掌握函数 极值概念讨论 优化问题。 基本可以通过 课程学习掌握 函数极值概念 讨论优化问题。 通过课程学习 掌握函数极值 概念讨论优化 问题有一定困 难。 对应用函数极 值概念讨论优 化问题掌握不 足。 课程目标 4 (20%) 熟练应用积分知 识归纳总结实验 数据。 能够应用积分 知识归纳总结 实验数据。 基本能够应用 积分知识归纳 总结实验数据。 应用积分知识 归纳总结实验 数据有一定困 难。 应用积分知识 归纳总结实验 数 据 掌 握 不 足。 课程目标 5 (20%) 能熟练应用定积 分表达一些几何 量与物理量的方 法。 能应用定积分 表达一些几何 量与物理量的 方法。 基本能应用定 积分表达一些 几何量与物理 量的方法。 应用定积分表 达一些几何量 与物理量的方 法 有 一 定 困 难。 应用定积分表 达一些几何量 与物理量的方 法掌握不足